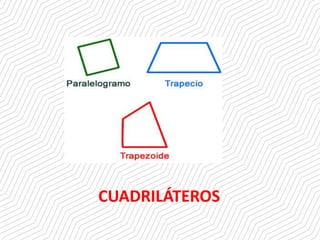
El documento clasifica los diferentes tipos de cuadriláteros. Los cuadriláteros se dividen en convexos y no convexos. Los cuadriláteros convexos incluyen paralelogramos (rombo, rectángulo, romboide), trapezoides y trapecios (isósceles, rectángulo, escaleno). Se proporcionan ejemplos y propiedades de cada tipo.

1. CUADRILÁTEROS

2. Cuadrilátero
• Un cuadrilátero es el polígono que tiene cuatro lados.
• Los cuadriláteros tienen distintas formas, pero todos ellos
tienen cuatro vértices y dos diagonales.

3. Cuadrilátero convexo Cuadrilátero no convexo o
cóncavo

4. Clasificación de los cuadriláteros convexos
I. PARALELOGRAMO
Es la figura que tiene los
lados opuestos paralelos dos a
dos.
Propiedades

5. 3. Rombo
Es un paralelogramo cuyos lados son
todos de igual medida.
4. Cuadrado
Es un paralelogramo cuyos lados tienen
igual medida y sus ángulos interiores
miden 90°.
1. Romboide
Es un paralelogramo cuyos ángulos
interiores no miden 90°.
2. Rectángulo
Es un paralelogramo cuyos ángulos
interiores miden 90°.
Clasificación de los Paralelogramos

6. II. TRAPEZOIDE
Es aquel cuadrilátero convexo que
no presenta lados opuestos
paralelos.
III. TRAPECIO
Es aquel cuadrilátero convexo que
solo tiene un par de lados opuestos
paralelos.
Propiedades:

7. Clasificación de los Trapecios
1. Trapecio isósceles
Es aquel trapecio cuyos lados no
paralelos son de igual longitud.
2. Trapecio rectángulo
Es aquel trapecio donde uno de sus
lados no paralelos es perpendicular a las
bases.
3. Trapecio escaleno
Es aquel trapecio cuyos lados no
paralelos son de diferente longitud.

8. Propiedades de los trapecios
1. En todo trapecio, la base media o
mediana es paralela a las bases y
su longitud es igual a la
semisuma de las longitudes de
sus bases.
2. En todo trapecio, el segmento que
une los puntos medios de las
diagonales es paralelo a las bases y
su longitud es igual a la
semidiferencia de las longitudes de
las bases.

9. Ejercicios
1. Calcula el valor de “x” en la figura
mostrada.
3x+15°
x+24°
x+16°
Resolución:
Por la suma de ángulos internos:
3x + 15° + x + 24° + 90° + x + 16° = 360°
5x = 215° → x = 43°
Rpta.: 43°
2. Calcula el valor de “x” en la figura
mostrada.
79°
x+4° 13°
2x
Resolución:
Tenemos que:
2x = x + 4° + 79° + 13° → x = 96°
Rpta.: 96°
3. Si ABCD es un romboide, calcula el valor de
“3x – 2y”.
Resolución:
En un romboide, los lados opuestos son de
igual longitud, entonces:
4x – 17 = x + 10 3y – 13 = 47 – 2y
3x = 27 5y = 60
x = 9 y = 12
Luego:
3x – 2y = 3(9) – 2(12) = 3
Rpta.: 3
4x-17 x+10
3y-13
47-2y
A
C
D
B

10. 4. Si ABCD es un trapecio y MN es su mediana,
calcula el valor de “x”.
Resolución:
Sabemos que: MN =
𝑩+𝒃
𝟐
Reemplazando los datos del gráfico:
24 =
𝒙+𝟖+𝒙+𝟐
𝟐
→ 24 = x + 5
x = 19
Rpta.: 19 cm
D
M
C
B
N
A
24 cm
x+2
x+8
5. Calcula el perímetro de un rombo ABCD, si
sus diagonales AC y BD miden 18 cm y 24 cm,
respectivamente.
Resolución:
Aplicamos el teorema de Pitágoras:
𝑳𝟐
= 𝟏𝟐𝟐
+ 𝟗𝟐
𝑳𝟐
= 𝟏𝟒𝟒 + 𝟖𝟏 = 𝟐𝟐𝟓→ 𝐋 = 𝟏𝟓
Luego, el perímetro es:
2p = 4(15) = 60
Rpta.: 60 cm
A
B
C
D
9
9
12
12
L