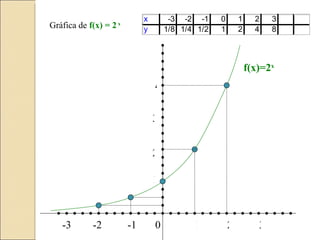
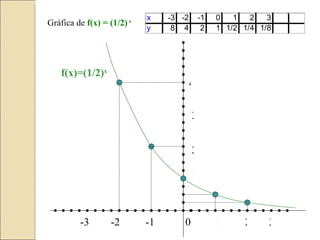
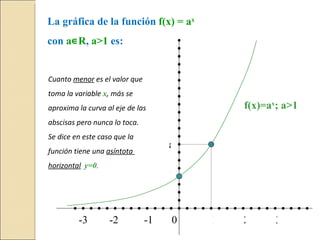
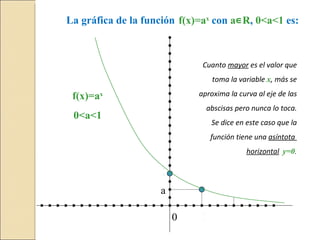
Este documento describe las funciones exponenciales, que tienen la forma f(x) = a^x donde a es un número real positivo distinto de 1 y k es un número real distinto de 0. Se explica que a es la base y k es el coeficiente. Se dan ejemplos de funciones exponenciales y sus gráficas correspondientes, y se describe que cuanto más grande o más pequeño es el valor de x, la curva se aproxima más al eje y=0 pero nunca lo toca, teniendo asíntotas horizontales.

1. LA FUNCIÓN EXPONENCIAL

2. Una función exponencial es una función de la forma: donde a es un número real positivo distinto de 1 y k un número real distinto de 0 . a se denomina base y k coeficiente de la función exponencial.

3. Veamos algunos ejemplos de funciones exponenciales y sus respectivas gráficas. f(x) = 2 x f(x) = (1/2) x

4. Gráfica de f(x) = 2 x f(x)=2 x 1 0 2 3 4 1 2 -1 -2 -3 3

5. 0 f(x)=(1/2) x Gráfica de f(x) = (1/2) x 1 1 2 2 3 4 -1 -2 -3 3

6. En general…

7. Cuanto menor es el valor que toma la variable x , más se aproxima la curva al eje de las abscisas pero nunca lo toca. Se dice en este caso que la función tiene una asíntota horizontal y=0 . 1 1 0 a 2 -1 -2 -3 3 f(x)=a x ; a>1 La gráfica de la función con a ∊ R , a>1 es: f(x) = a x

8. Cuanto mayor es el valor que toma la variable x , más se aproxima la curva al eje de las abscisas pero nunca lo toca. Se dice en este caso que la función tiene una asíntota horizontal y=0 . 1 1 0 a f(x)=a x 0<a<1 La gráfica de la función f(x)=a x con a ∊ R , 0<a<1 es: