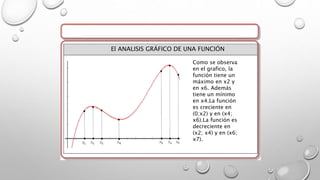
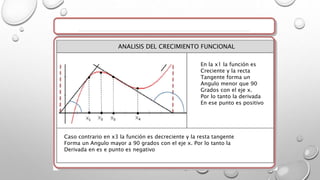
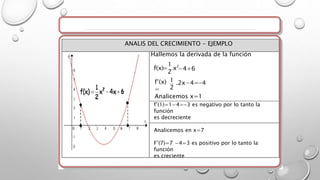
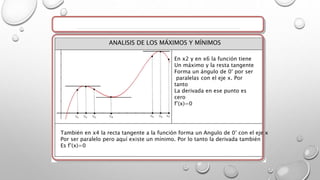
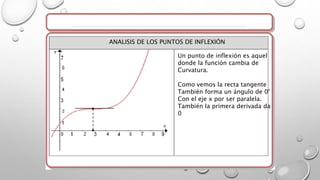
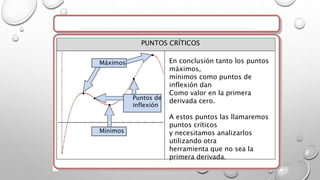
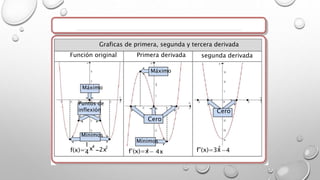
Este documento presenta los conceptos básicos de las derivadas y su interpretación geométrica. Explica que la pendiente de la recta tangente es igual al límite de la derivada cuando el incremento tiende a cero. También define la derivada como este límite y analiza gráficamente el crecimiento de funciones, identificando puntos máximos, mínimos y de inflexión donde la derivada es cero. Finalmente, explica que en estos puntos críticos se debe analizar la segunda derivada.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO DE TECNOLOGÍA
“ANTONIO JOSÉ DE SUCRE”
EXTENSION BARQUISIMETO
Alumno:
José Silva
C.I:26.831.554

2. Aplicaciones de las derivadas
INTERPRETACION GEOMETRICA
La pendiente de la RECTA
SECANTE es igual a la
tangente trigonométrica de
α.
tga=
La recta tangente es
aquella que corta a una
curva en dos o mas puntos.
ˆ
Recta Secante
∆y
∆x ∆x
=
F(x+∆x)-f(x)
∆x

3. La pendiente de la recta
tangente es igual a límite
cuando ∆ x tiende acero del
cociente incremental.
Recta Tangente
∆y
∆x
Lim
∆x 0
=
f(x+ ∆x)-f(x)
∆x
Lim
∆x 0=tgaˆ
A esta expresión lo
conoceremos como derivada.
INTERPRETACION GEOMETRICA
Aplicaciones de las derivadas

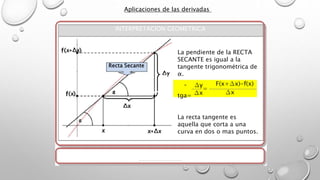
4. La derivada de una función
es igual al límite cuando el
incremento (∆ x) tiende
acero del cociente
incremental de la diferencia
de la función incrementada
[f(x+ ∆ x)]menos la función
[f(x)] sin incrementar dividido
el incremento (∆ x).
DEFINICION
Aplicaciones de las derivadas
∆y
∆x
f(x+∆x)-f(x)
∆x
Lim
∆x 0=
Lim
∆x 0
=y′

5. Como se observa
en el grafico, la
función tiene un
máximo en x2 y
en x6. Además
tiene un mínimo
en x4.La función
es creciente en
(0;x2) y en (x4;
x6).La función es
decreciente en
(x2; x4) y en (x6;
x7).
El ANALISIS GRÁFICO DE UNA FUNCIÓN

6. En la x1 la función es
Creciente y la recta
Tangente forma un
Angulo menor que 90
Grados con el eje x.
Por lo tanto la derivada
En ese punto es positivo
Caso contrario en x3 la función es decreciente y la resta tangente
Forma un Angulo mayor a 90 grados con el eje x. Por lo tanto la
Derivada en es e punto es negativo
ANALISIS DEL CRECIMIENTO FUNCIONAL

7. Hallemos la derivada de la función
f(x)=
1
2
x2
−4+6
f′(x)
=
1
2
.2x−4=-4
Analicemos x=1
f′(1)=1−4=-3 es negativo por lo tanto la
función
es decreciente
Analicemos en x=7
F’(7)=7 −4=3 es positivo por lo tanto la
función
es creciente
ANALIS DEL CRECIMIENTO - EJEMPLO

8. En x2 y en x6 la función tiene
Un máximo y la resta tangente
Forma un ángulo de 0° por ser
paralelas con el eje x. Por
tanto
La derivada en ese punto es
cero
f’(x)=0
También en x4 la recta tangente a la función forma un Angulo de 0° con el eje x
Por ser paralelo pero aquí existe un mínimo. Por lo tanto la derivada también
Es f’(x)=0
ANALISIS DE LOS MÁXIMOS Y MÍNIMOS

9. Un punto de inflexión es aquel
donde la función cambia de
Curvatura.
Como vemos la recta tangente
También forma un ángulo de 0°
Con el eje x por ser paralela.
También la primera derivada da
0
ANALISIS DE LOS PUNTOS DE INFLEXIÓN

10. En conclusión tanto los puntos
máximos,
mínimos como puntos de
inflexión dan
Como valor en la primera
derivada cero.
A estos puntos las llamaremos
puntos críticos
y necesitamos analizarlos
utilizando otra
herramienta que no sea la
primera derivada.
Máximos
Puntos de
inflexión
Mínimos
PUNTOS CRÍTICOS

11. Máximo
Máximo
Puntos de
inflexión
Cero
Cero
Mínimos
Mínimos
f(x)=
1
4
x4
−2x2
f’(x)=x3
− 4x f”(x)=3x
2
−4
Graficas de primera, segunda y tercera derivada
Función original Primera derivada segunda derivada