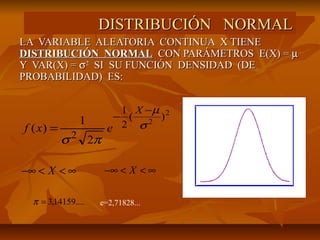
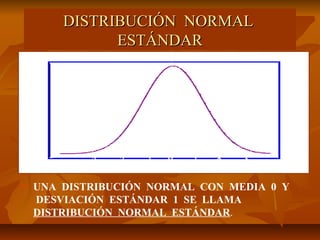
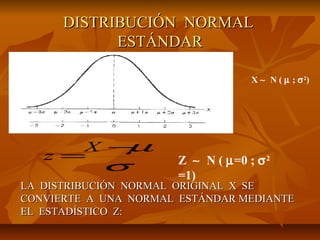
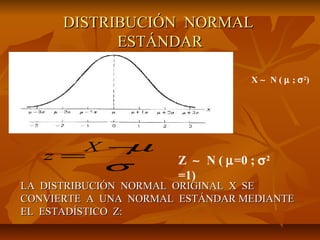
La distribución normal describe una variable aleatoria continua donde la función de densidad de probabilidad es una curva en forma de campana. La distribución normal tiene dos parámetros: la media (μ) y la varianza (σ2). La distribución normal estándar tiene una media de 0 y una varianza de 1. Cualquier distribución normal puede convertirse a una distribución normal estándar usando la transformación z = (x - μ)/ σ.

1. DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL

2. LA VARIABLE ALEATORIA CONTINUA X TIENELA VARIABLE ALEATORIA CONTINUA X TIENE
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL CON PARÁMETROS E(X) =CON PARÁMETROS E(X) = µµ
Y VAR(X) =Y VAR(X) = σσ22
SI SU FUNCIÓN DENSIDAD (DESI SU FUNCIÓN DENSIDAD (DE
PROBABILIDAD) ES:PROBABILIDAD) ES:
2
2
)(
2
1
2
2
1
)( σ
µ
πσ
−
−
=
X
exf
∞<<−∞ X ∞<<−∞ X
....14159,3=π e=2,71828...
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL

3. µ=Mediana=Moda
MEDIA = MEDIANA = MODAMEDIA = MEDIANA = MODA
ESES SIMÉTRICASIMÉTRICA RESPECTO A SU MEDIA EN LA CUALRESPECTO A SU MEDIA EN LA CUAL
TIENE SU MÁXIMO.TIENE SU MÁXIMO.
CARACTERÍSTICAS DE UNACARACTERÍSTICAS DE UNA
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL
X

4. −3 −2 0 21
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL
ESTÁNDARESTÁNDAR
• UNA DISTRIBUCIÓN NORMAL CON MEDIA 0 Y
DESVIACIÓN ESTÁNDAR 1 SE LLAMA
DISTRIBUCIÓN NORMAL ESTÁNDAR.
−1 3

5. X ∼ N ( µ ; σ2
)
σ
µ−
=
X
z Z ∼ N ( µ=0 ; σ2
=1)
LA DISTRIBUCIÓN NORMAL ORIGINAL X SELA DISTRIBUCIÓN NORMAL ORIGINAL X SE
CONVIERTE A UNA NORMAL ESTÁNDAR MEDIANTECONVIERTE A UNA NORMAL ESTÁNDAR MEDIANTE
EL ESTADÍSTICO Z:EL ESTADÍSTICO Z:
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL
ESTÁNDARESTÁNDAR

6. X ∼ N ( µ ; σ2
)
σ
µ−
=
X
z Z ∼ N ( µ=0 ; σ2
=1)
LA DISTRIBUCIÓN NORMAL ORIGINAL X SELA DISTRIBUCIÓN NORMAL ORIGINAL X SE
CONVIERTE A UNA NORMAL ESTÁNDAR MEDIANTECONVIERTE A UNA NORMAL ESTÁNDAR MEDIANTE
EL ESTADÍSTICO Z:EL ESTADÍSTICO Z:
DISTRIBUCIÓN NORMALDISTRIBUCIÓN NORMAL
ESTÁNDARESTÁNDAR