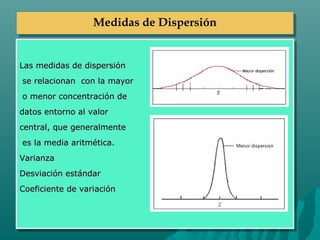
Este documento describe diferentes medidas de dispersión y posición. Explica que los percentiles dividen una población en partes iguales, los deciles en 10 partes, los quintiles en 5 partes y los cuartiles en 4 partes. Luego describe que las medidas de dispersión como la varianza, desviación estándar y coeficiente de variación miden qué tan concentrados o dispersos están los datos respecto al valor central, generalmente la media. Finalmente explica que la varianza mide la suma de las desviaciones al cuadrado respecto a la media, la desviación estándar es su raí

1. Patricia Santana Mancilla
MEDIDAS
DE DISPERSIÓN

2. Percentiles
Son valores que dividen a la población o muestra en partes
iguales. En este caso se divide en 100 partes iguales, donde cada
uno contiene el 1% de las observaciones y son 99 percentiles.
Percentiles
Son valores que dividen a la población o muestra en partes
iguales. En este caso se divide en 100 partes iguales, donde cada
uno contiene el 1% de las observaciones y son 99 percentiles.
Medidas de PosiciónMedidas de Posición

3. Donde:
Deciles: Se dividen en 10 partes iguales, D1, D2,…, D9.
Quintiles: Se dividen en 5 partes iguales, K1, K2, K3 y K4.
Cuartiles: Se dividen en 4 partes iguales, Q1, Q2 y Q3.
Donde:
Deciles: Se dividen en 10 partes iguales, D1, D2,…, D9.
Quintiles: Se dividen en 5 partes iguales, K1, K2, K3 y K4.
Cuartiles: Se dividen en 4 partes iguales, Q1, Q2 y Q3.

4. Las medidas de dispersiónLas medidas de dispersión
se relacionan con la mayorse relacionan con la mayor
o menor concentración deo menor concentración de
datos entorno al valordatos entorno al valor
central, que generalmentecentral, que generalmente
es la media aritmética.es la media aritmética.
VarianzaVarianza
Desviación estándarDesviación estándar
Coeficiente de variaciónCoeficiente de variación
Las medidas de dispersiónLas medidas de dispersión
se relacionan con la mayorse relacionan con la mayor
o menor concentración deo menor concentración de
datos entorno al valordatos entorno al valor
central, que generalmentecentral, que generalmente
es la media aritmética.es la media aritmética.
VarianzaVarianza
Desviación estándarDesviación estándar
Coeficiente de variaciónCoeficiente de variación
Medidas de DispersiónMedidas de Dispersión

5. Varianza: Es la suma de las desviaciones de las
observaciones con respecto a la media, dividida por el
número de observaciones.
Mientras mayor es el valor de la varianza, mayor es la
dispersión de las observaciones.
Varianza: Es la suma de las desviaciones de las
observaciones con respecto a la media, dividida por el
número de observaciones.
Mientras mayor es el valor de la varianza, mayor es la
dispersión de las observaciones.

6. Propiedades de la Varianza:
1. La varianza de una constante es igual a 0.
2. La varianza es no negativa mayor o igual a cero.
3. La varianza no se altera al sumarle una constante.
4. La varianza del producto de una variable por una constante, es igual
al cuadrado de la constante multiplicado por la varianza de la
variable.
V (a Y) = a² V(y)
Propiedades de la Varianza:
1. La varianza de una constante es igual a 0.
2. La varianza es no negativa mayor o igual a cero.
3. La varianza no se altera al sumarle una constante.
4. La varianza del producto de una variable por una constante, es igual
al cuadrado de la constante multiplicado por la varianza de la
variable.
V (a Y) = a² V(y)

7. Desviación Estándar:
La raíz cuadrada de la varianza.
Desviación Estándar:
La raíz cuadrada de la varianza.

8. Coeficiente de Variación:
Es un recurso que sirve para comparar la variación de dos
series de datos que están medidos en diferentes unidades
(estatura y peso).
Se expresa en porcentaje.
Coeficiente de Variación:
Es un recurso que sirve para comparar la variación de dos
series de datos que están medidos en diferentes unidades
(estatura y peso).
Se expresa en porcentaje.