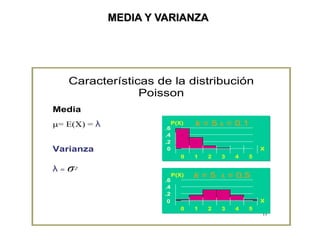
La distribución de Poisson lleva el nombre de Simeón Denis Poisson, un matemático francés que describió esta distribución de probabilidad discreta. Se utiliza para procesos aleatorios donde los eventos son independientes y ocurren con baja frecuencia, como accidentes o defectos en productos. La distribución de Poisson depende de un parámetro λ que representa la media y la varianza del número de eventos.

1. La distribución de Poisson se llama así
en honor a su creador, el francés
Simeón Dennis Poisson (1781-1840),
Esta distribución de probabilidades fue
uno de los múltiples trabajos matemáticos
que Dennis completó en su productiva trayectoria.
(Astronauta francés)

4. P(x) = µx * e-µ
x !
=

5. • La distribución de Poisson se utiliza en situaciones donde los
sucesos son impredecibles o de ocurrencia aleatoria. En otras
palabras no se sabe el total de posibles resultados.
• Permite determinar la probabilidad de ocurrencia de un suceso
con resultado discreto.
• Es muy útil cuando la muestra o segmento n es grande y la
probabilidad de éxitos p es pequeña.
• Se utiliza cuando la probabilidad del evento que nos interesa se
distribuye dentro de un segmento n dado como por ejemplo
distancia, área, volumen o tiempo definido.
La distribución de Poisson se emplea para
describir procesos con un elemento en común,
pueden ser descritos por una variable
aleatoria discreta.

6. 1. La probabilidad de observar exactamente un éxito en el
segmento o tamaño de muestra n es constante.
2. El evento debe considerarse un suceso raro.
3. El evento debe ser aleatorio e independiente de otros
eventos
PROPIEDADES
Si repetimos el experimento n veces podemos
obtener resultados para la construcción de la
distribución de Poisson.

7. La distribución de probabilidad de Poisson es un ejemplo de
distribución de probabilidad discreta.
La distribución de Poisson parte de la distribución binomial.
Cuando en una distribución binomial se realiza el experimento
muchas veces, la muestra n es grande y la probabilidad de
éxito p en cada ensayo es baja, es aquí donde aplica el
modelo de distribución de Poisson.
Se tiene que cumplir que:
p < 0.10
p * n < 10

8. La probabilidad de que haya un accidente en una compañía de
manufactura es de 0.02 por cada día de trabajo. Si se trabajan 300
días al año, ¿cuál es la probabilidad de tener 3 accidentes?
Como la probabilidad p es menor que 0.1, y el producto n * p es
menor que 10 (300 * 0.02 = 6), entonces, aplicamos el modelo de
distribución de Poisson:
Al realizar el cómputo tenemos que P(x = 3) = 0.0892
Por lo tanto, la probabilidad de tener 3 accidentes laborales en 300
días de trabajo es de 8.9%.
EJEMPLO
P(x) = µx * e-µ
x!
=
µ = 6

9. La probabilidad de que un producto salga defectuoso es de
0.012. ¿Cuál es la probabilidad de que entre 800 productos ya
fabricados hayan 5 defectuosos?
En este ejemplo vemos nuevamente la probabilidad p menor
que 0.1, y el producto n * p menor que 10, por lo que
aplicamos el modelo de distribución de Poisson:
El resultado es P (x = 5) = 0.04602
Por lo tanto, la probabilidad de que haya 5 productos
defectuosos entre 800 recién producidos es de 4.6%.
P(x) = µx * e-µ
x!
µ = 0.012 * 800 = 9.6
=

10. 17
Características de la distribución
Poisson
k = 5 λ = 0.1
k = 5 λ = 0.5
Media
= E(X) = λ
Varianza
λ = σ2
0
.2
.4
.6
0 1 2 3 4 5
X
P(X)
.2
.4
.6
0 1 2 3 4 5
X
P(X)
0
MEDIA Y VARIANZA

11. Un comerciante de verduras tiene conocimiento de que el 3%
de la caja está descompuesta. Si un comprador elige 100
verduras al azar, encuentre la probabilidad de que,
a) las 4 estén descompuestas.
b) de 1 a 3 estén descompuestas
Para resolver la pregunta “b” repase el
módulo de las reglas de probabilidad.
En este caso se resuelve sumando las
probabilidades P(x=1) + P(x=2) + P(x=3)
= 0.1494 + 0.2240 + 0.2240
TRABAJA LAS PROBABILIDADES DE 1, 2 Y 3
Use fórmula y compruebe en Excel

12. EJERCICIO
En una tienda de telas un promedio de 12 personas por hora le hacen
preguntas a un decorador. Cuál es la probabilidad de que 3 o más personas
se acerquen al decorador para hacerle preguntas en un periodo de 10
minutos.
OJO: 12 / 60 = 0.2 por minuto = 0.2 * 10 = 2
VARIAS FORMAS DE SOLUCION
a) Sacar P(3) + P(4) ……….
b) Sacar P(0)+ P(1) + P(2) a ese resultado debe restarlo de uno
c) En Excel , sacar P(2) acumulado y ese valor restarlo de 1
0.6766 (ACUMULADO HASTA 2) ENTONCES 1 – 0.6766 = 0.323