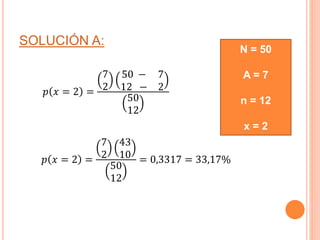
Este documento trata sobre la distribución hipergeométrica, una distribución de probabilidad discreta aplicable a muestreos aleatorios sin reemplazo de una población finita. Explica que la distribución hipergeométrica considera una población dividida en dos grupos, uno de "éxitos" y otro de "fracasos", y presenta la fórmula para calcular la probabilidad hipergeométrica. También incluye un ejemplo numérico para ilustrar cómo aplicar la fórmula.

1. ESTADÍSTICA
HIPERGEOMETRICA
SINDY PAOLA OSSA VEGA
DIEGO ARMANDO SANCHEZ MORENO
INGENIERIA DE SISTEMAS
V SEMESTRE
2013

2. CONCEPTO Y APLICACIÓN
En teoría de la probabilidad la distribución
hipergeométrica es una distribución discreta
relacionada con muestreos aleatorios y sin
reemplazo.
La distribución hipergeométrica considera el caso en
el cual una población finita se divide en dos grupos,
uno de los cuales se considera "éxitos" y el otro
"Fracasos”.
La distribución hipergeométrica es aplicable a
muestreos sin reemplazo en una población finita.

3. CARACTERÍSTICAS
 La información de la muestra se toma sin
reposición de una población finita.
 La probabilidad de éxito no es constante. Cambia
para cada observación.
 El resultado de una prueba es dependiente de la
prueba anterior, siempre se vera afectado por el
resultado de observaciones previas.
 El tamaño de la muestra (n) debe ser superior en
un 5% con respecto al tamaño poblacional (N).
 La distribución es adecuada. Cuando el tamaño de
la población es pequeña.

4. FORMULA
𝑝 𝑥 =
𝐴
𝑥
𝑁 − 𝐴
𝑛 − 𝑥
𝑁
𝑛
La formula que se debe emplear para la distribución hipergeometrica es:
Siendo:
P(x)= probabilidad hipergeometrica que
se va a calcular para un valor dado de
x.
N= Tamaño de la población.
A= Numero de éxitos en la población
n= Tamaño de la muestra
x= Numero de éxitos en la muestra
Es necesario tener en cuenta que x no pude exceder a A ni a n.
Recordemos que:
𝐴
𝑥
=
𝐴!
𝐴 − 𝑥 ! ∗ 𝑥!
𝑁
𝑛
=
𝑁!
𝑁−𝑛 !∗𝑛!

5. EJERCICIO
En la producción de mouses inalámbricos, por cada
50 fabricados, 43 están en excelente estado. Si se
toma una muestra de 12 artículos, cual es la
probabilidad:
A- de que exactamente 2 no sean clasificados como
excelentes
B- de que 10 sean clasificados como excelentes

6. SOLUCIÓN A:
𝑝 𝑥 = 2 =
7
2
50 − 7
12 − 2
50
12
𝑝 𝑥 = 2 =
7
2
43
10
50
12
= 0,3317 = 33,17%
N = 50
A = 7
n = 12
x = 2

7. SOLUCION B:
𝑝 𝑥 = 10 =
43
10
50 − 43
12 − 10
50
12
𝑝 𝑥 = 10 =
43
10
7
2
50
12
P(X=10)= 0,3317= 33,17
N = 50
A = 43
n = 12
x = 10

8. GRACIAS