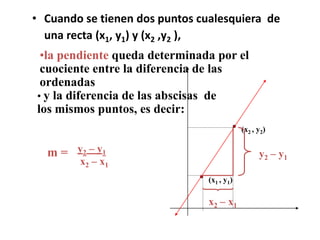
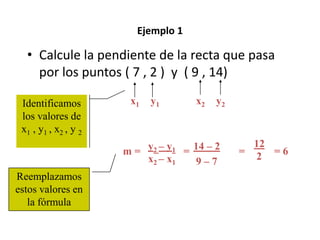
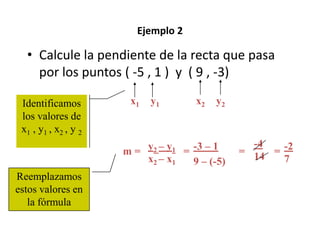
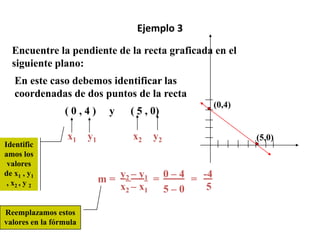
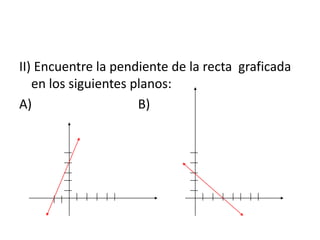
El documento explica cómo calcular la pendiente de una recta a partir de dos puntos que la definen. La fórmula para calcular la pendiente es m = (y2 - y1) / (x2 - x1), donde (x1, y1) y (x2, y2) son las coordenadas de los dos puntos. El documento provee tres ejemplos para ilustrar cómo aplicar la fórmula y también incluye ejercicios para practicar el cálculo de pendientes.

1. Cálculo de la pendiente de una recta

2. Cuando se tienen dos puntos cualesquiera de una recta (x1, y1) y (x2 ,y2 ),la pendiente queda determinada por el cuociente entre la diferencia de las ordenadas

3. y la diferencia de las abscisas de los mismos puntos, es decir:(x2 , y2)y2 – y1m =y2 – y1x2 – x1(x1 , y1)x2 – x1

4. Ejemplo 1Calcule la pendiente de la recta que pasa por los puntos ( 7 , 2 ) y ( 9 , 14)x1y1x2y2Identificamos los valores de x1 , y1 , x2 , y 212y2 – y114 – 2 m ==== 62x2 – x19 – 7 Reemplazamos estos valores en la fórmula

5. Ejemplo 2Calcule la pendiente de la recta que pasa por los puntos ( -5 , 1 ) y ( 9 , -3)x1y1x2y2Identificamos los valores de x1 , y1 , x2 , y 2-4y2 – y1-3 – 1 -2m ====14x2 – x179 – (-5) Reemplazamos estos valores en la fórmula

6. Ejemplo 3Encuentre la pendiente de la recta graficada en el siguiente plano: En este caso debemos identificar las coordenadas de dos puntos de la recta(0,4)( 0 , 4 ) y ( 5 , 0)x1y1x2y2(5,0)Identificamos los valores de x1 , y1 , x2 , y 2y2 – y10 – 4 -4m ===x2 – x1 55 – 0 Reemplazamos estos valores en la fórmula

7. Ejercicio 2I) Calcule la pendiente de la recta que pasa por los puntos:A) (3 , -6) y (-2 , -2)B) (7 , -9) y (0 , -1)C) (-3 , -4) y el origenD) (3 , -4) y ( 2 , -6)