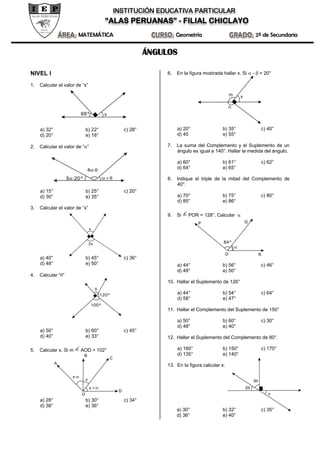
Este documento contiene 16 problemas de ángulos en dos niveles de dificultad. Los problemas involucran conceptos como calcular valores de ángulos desconocidos, hallar complementos, suplementos, bisectrices y sumas/diferencias de ángulos. El objetivo es que el estudiante practique cálculos angulares y aplique sus conocimientos de geometría para resolver cada problema.

1. ÁNGULOS
NIVEL I
1. Calcular el valor de “x”
a) 32° b) 22° c) 28°
d) 20° e) 18°
2. Calcular el valor de “ ”
a) 15° b) 25° c) 20°
d) 30° e) 35°
3. Calcular el valor de “x”
a) 40° b) 45° c) 36°
d) 48° e) 50°
4. Calcular “ ”
a) 50° b) 60° c) 45°
d) 40° e) 33°
5. Calcular x. Si m AOD = 102°
a) 28° b) 30° c) 34°
d) 38° e) 36°
6. En la figura mostrada hallar x. Si - = 20°
a) 20° b) 35° c) 40°
d) 45 e) 55°
7. La suma del Complemento y el Suplemento de un
ángulo es igual a 140°. Hallar la medida del ángulo.
a) 60° b) 61° c) 62°
d) 64° e) 65°
8. Indique el triple de la mitad del Complemento de
40°.
a) 70° b) 75° c) 80°
d) 85° e) 86°
9. Si POR = 128°. Calcular
a) 44° b) 56° c) 46°
d) 48° e) 50°
10. Hallar el Suplemento de 126°
a) 44° b) 54° c) 64°
d) 58° e) 47°
11. Hallar el Complemento del Suplemento de 150°
a) 50° b) 60° c) 30°
d) 48° e) 40°
12. Hallar el Suplemento del Complemento de 80°.
a) 160° b) 150° c) 170°
d) 135° e) 140°
13. En la figura calcular x:
a) 30° b) 32° c) 35°
d) 36° e) 40°
MATEMÁTICA Geometría 2º de Secundaria
“ALAS PERUANAS” - FILIAL CHICLAYO
INSTITUCIÓN EDUCATIVA PARTICULAR

2. 14. Calcular la medida de un ángulo sabiendo que el
suplemento del triple del Complemento de su
medida, es igual a la misma medida.
a) 45° b) 30° c) 60°
d) 40° e) 36°
15. Si el complemento de la medida de un ángulo, es al
Suplemento de su misma medida como 2 es a 5.
Calcular dicha medida.
a) 27° b) 36° c) 18°
d) 60° e) 30°
16. Calcular la medida de un ángulo sabiendo que el
complemento de su medida es igual a la mitad de la
misma medida.
a) 30° b) 45° c) 75°
d) 80° e) 60°
NIVEL II
1. Del gráfico m BOC = 72°. Calcular la medida del
ángulo formado por las bisectrices de AOB y COD.
a) 120° b) 126° c) 130°
d) 132° e) 135°
2. Hallar “x”. Si OB es bisectriz del ángulo AOC.
a) 20° b) 10° c) 12°
d) 14° e) 30°
3. Se tienen los ángulos adyacentes AOˆ B y BOˆ C
que se diferencian en 48°. Calcular la medida del
ángulo formado por la bisectriz del ángulo AOC y el
rayo OB
a) 48° b) 24° c) 18°
d) 12° e) 6°
4. Se tienen los ángulos consecutivos AOˆ B, BOˆ C y C
Oˆ D, tal que m AOC= BOD=90°. Hallar la
medida del ángulo formado por las bisectrices de A
Oˆ B y C Oˆ D.
a) 80° b) 82° c) 85°
d) 88° e) 90°
5. En la figura hallar m MOC. Si m BOC- m AOC
= 40°. Además OM bisectriz del ángulo AOB.
a) 12° b) 15° c) 18°
d) 20° e) 36°
6. Dados los ángulos consecutivos A Oˆ B y B Oˆ C. Si
m AOB + m AOC = 118°
Hallar m AOM. Siendo OM la bisectriz de BOˆ C.
a) 59° b) 28° c) 36°
d) 46° e) 48°
7. SI m BOD = 120°. Hallar la medida del ángulo
formado por las bisectrices de A Oˆ B y C Oˆ D.
a) 90° b) 100° c) 110°
d) 120° e) 105°
8. Hallar m MON. Si m AOC=120° y OM es
bisectriz de AOB.
a) 30° b) 40° c) 45°
d) 20° e) 60°
9. En la figura. Calcular “x”
a) 10°
b) 15°
c) 20°
d) 25°
e) 30°

3. 10. En la figura, calcular la m BOD. Si m AOC = 100°
y m XOY = 80°
a) 50° b) 90° c) 70°
d) 60° e) 120°
11. Hallar la medida del ángulo formado por las
bisectrices de A Oˆ B y B Oˆ C.
a) 30°
b) 60°
c) 45°
d) 37°
e) 53°
12. En la figura calcular “x”
a) 20°
b) 10°
c) 12°
d) 15°
e) 18°
13. En la figura calcular la medida del ángulo formado
por las bisectrices de los ángulos AOB y COD.
a) 150° b) 115° c) 105°
d) 125° e) 135°
14. Se tienen los ángulos adyacentes AOB y BOC tal
que m AOB = 40°. Calcular la medida del ángulo
que forman las bisectrices de los ángulos AOC y
BOC.
a) 20° b) 40° c) 30°
d) 25° e) 10°
15. Se tienen los ángulos adyacentes AOB y BOC de
modo que m AOB - m BOC = 48°. Luego se
trazan las bisectrices OM del AOB, ON del
BOC y OS del MON. Calcular la m SOB.
a) 48° b) 32° c) 18°
d) 24° e) 12°
16. Calcular la medida de un ángulo sabiendo que el
Suplemento del Complemento de su medida es
igual al séxtuplo de la misma medida.
a) 12° b) 15° c) 18°
d) 20° e) 30°