Descargado 29 veces
Subido porRAFAEL CORTINA RODRÍGUEZ
Ejercicios sobre el punto de equilibrio
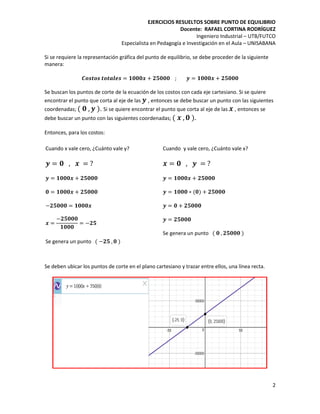
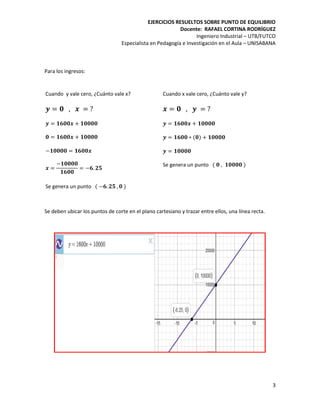
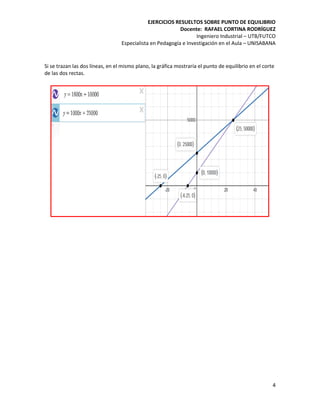
El documento proporciona un análisis detallado del punto de equilibrio de una empresa, donde los costos variables son de $1000 por unidad y los costos fijos son de $25000. Se establecen las ecuaciones de ingresos y costos, encontrándose un punto de equilibrio en 25 unidades, con ingresos totales de $50000 y costos totales de $50000. Además, se explican las representaciones gráficas de estas ecuaciones y cómo encontrar los puntos de corte en el plano cartesiano.
Más contenido relacionado
Similar a Ejercicios sobre el punto de equilibrio
Más de RAFAEL CORTINA RODRÍGUEZ
Ejercicios sobre el punto de equilibrio
- 1. EJERCICIOS RESUELTOS SOBREPUNTO DE EQUILIBRIO Docente: RAFAEL CORTINA RODRÍGUEZ Ingeniero Industrial – UTB/FUTCO Especialista en Pedagogía e Investigación en el Aula – UNISABANA 1 Los costos de una empresa se encuentran discriminados de la siguiente manera: Costos variables por valor de $ 1000 por cada unidad y los costos fijos son equivalentes a $ 25000. Por su parte, los ingresos fijos tienen un valor de $ 10000 y los ingresos variables equivalen a $ 1600 por unidad vendida. Halle las ecuaciones de ingresos, de costos y determine el punto de equilibrio. Teniendo en cuenta la información recibida, se puede concluir que los costos variables se pueden definir como 𝑪𝒐𝒔𝒕𝒐𝒔 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 = 𝟏𝟎𝟎𝟎𝒙 ; es decir, $ 𝟏𝟎𝟎𝟎 𝒑𝒆𝒔𝒐𝒔 𝒑𝒐𝒓 𝒖𝒏𝒊𝒅𝒂𝒅 𝒇𝒂𝒃𝒓𝒊𝒄𝒂𝒅𝒂. Entonces, los costos totales quedarían definidos así: 𝑪𝒐𝒔𝒕𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝑪𝒐𝒔𝒕𝒐𝒔 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 + 𝑪𝒐𝒔𝒕𝒐𝒔 𝒇𝒊𝒋𝒐𝒔 𝑪𝒐𝒔𝒕𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 Así mismo, se puede decir que los ingresos variables corresponden a: 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 = $ 𝟏𝟔𝟎𝟎 𝒑𝒐𝒓 𝒖𝒏𝒊𝒅𝒂𝒅 𝒗𝒆𝒏𝒅𝒊𝒅𝒂 Entonces, los ingresos totales quedarían definidos así: 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 + 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒇𝒊𝒋𝒐𝒔 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝟏𝟔𝟎𝟎𝒙 + 𝟏𝟎𝟎𝟎𝟎 El punto de equilibrio se considera cuando los costos totales son exactamente iguales a los ingresos totales, por lo tanto: 𝑰𝒏𝒈𝒓𝒆𝒔𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝑪𝒐𝒔𝒕𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 1600𝑥 + 10000 = 1000𝑥 + 25000 1600𝑥 − 1000𝑥 = 25000 − 10000 600𝑥 = 15000 𝑥 = 15000 600 ; 𝒙 = 𝟐𝟓 ; 𝒙 = 𝟐𝟓 𝒖𝒏𝒊𝒅𝒂𝒅𝒆𝒔 𝐼𝑛𝑔𝑟𝑒𝑠𝑜𝑠 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = 1600𝑥 + 10000 𝐼𝑛𝑔. 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = 1600 ∗ (25) + 10000 𝐼𝑛𝑔. 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = $ 40000 + 10000 𝑰𝒏𝒈. 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = $ 𝟓𝟎𝟎𝟎𝟎 𝐶𝑜𝑠𝑡𝑜𝑠 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = 1000𝑥 + 25000 𝐶𝑜𝑠𝑡𝑜𝑠 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = 1000 ∗ (25) + 25000 𝐶𝑜𝑠𝑡𝑜𝑠 𝑡𝑜𝑡𝑎𝑙𝑒𝑠 = 25000 + 25000 𝑪𝒐𝒔𝒕𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝟓𝟎𝟎𝟎𝟎
- 2. EJERCICIOS RESUELTOS SOBREPUNTO DE EQUILIBRIO Docente: RAFAEL CORTINA RODRÍGUEZ Ingeniero Industrial – UTB/FUTCO Especialista en Pedagogía e Investigación en el Aula – UNISABANA 2 Si se requiere la representación gráfica del punto de equilibrio, se debe proceder de la siguiente manera: 𝑪𝒐𝒔𝒕𝒐𝒔 𝒕𝒐𝒕𝒂𝒍𝒆𝒔 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 ; 𝒚 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 Se buscan los puntos de corte de la ecuación de los costos con cada eje cartesiano. Si se quiere encontrar el punto que corta al eje de las 𝒚 , entonces se debe buscar un punto con las siguientes coordenadas; ( 𝟎 , 𝒚 ). Si se quiere encontrar el punto que corta al eje de las 𝒙 , entonces se debe buscar un punto con las siguientes coordenadas; ( 𝒙 , 𝟎 ). Entonces, para los costos: Cuando x vale cero, ¿Cuánto vale y? 𝒚 = 𝟎 , 𝒙 = ? 𝒚 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 𝟎 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 −𝟐𝟓𝟎𝟎𝟎 = 𝟏𝟎𝟎𝟎𝒙 𝒙 = −𝟐𝟓𝟎𝟎𝟎 𝟏𝟎𝟎𝟎 = −𝟐𝟓 Se genera un punto ( −𝟐𝟓 , 𝟎 ) Cuando y vale cero, ¿Cuánto vale x? 𝒙 = 𝟎 , 𝒚 = ? 𝒚 = 𝟏𝟎𝟎𝟎𝒙 + 𝟐𝟓𝟎𝟎𝟎 𝒚 = 𝟏𝟎𝟎𝟎 ∗ (𝟎) + 𝟐𝟓𝟎𝟎𝟎 𝒚 = 𝟎 + 𝟐𝟓𝟎𝟎𝟎 𝒚 = 𝟐𝟓𝟎𝟎𝟎 Se genera un punto ( 𝟎 , 𝟐𝟓𝟎𝟎𝟎 ) Se deben ubicar los puntos de corte en el plano cartesiano y trazar entre ellos, una línea recta.
- 3. EJERCICIOS RESUELTOS SOBREPUNTO DE EQUILIBRIO Docente: RAFAEL CORTINA RODRÍGUEZ Ingeniero Industrial – UTB/FUTCO Especialista en Pedagogía e Investigación en el Aula – UNISABANA 3 Para los ingresos: Cuando y vale cero, ¿Cuánto vale x? 𝒚 = 𝟎 , 𝒙 = ? 𝒚 = 𝟏𝟔𝟎𝟎𝒙 + 𝟏𝟎𝟎𝟎𝟎 𝟎 = 𝟏𝟔𝟎𝟎𝒙 + 𝟏𝟎𝟎𝟎𝟎 −𝟏𝟎𝟎𝟎𝟎 = 𝟏𝟔𝟎𝟎𝒙 𝒙 = −𝟏𝟎𝟎𝟎𝟎 𝟏𝟔𝟎𝟎 = −𝟔. 𝟐𝟓 Se genera un punto ( −𝟔. 𝟐𝟓 , 𝟎 ) Cuando x vale cero, ¿Cuánto vale y? 𝒙 = 𝟎 , 𝒚 = ? 𝒚 = 𝟏𝟔𝟎𝟎𝒙 + 𝟏𝟎𝟎𝟎𝟎 𝒚 = 𝟏𝟔𝟎𝟎 ∗ (𝟎) + 𝟏𝟎𝟎𝟎𝟎 𝒚 = 𝟏𝟎𝟎𝟎𝟎 Se genera un punto ( 𝟎 , 𝟏𝟎𝟎𝟎𝟎 ) Se deben ubicar los puntos de corte en el plano cartesiano y trazar entre ellos, una línea recta.
- 4. EJERCICIOS RESUELTOS SOBREPUNTO DE EQUILIBRIO Docente: RAFAEL CORTINA RODRÍGUEZ Ingeniero Industrial – UTB/FUTCO Especialista en Pedagogía e Investigación en el Aula – UNISABANA 4 Si se trazan las dos líneas, en el mismo plano, la gráfica mostraría el punto de equilibrio en el corte de las dos rectas.