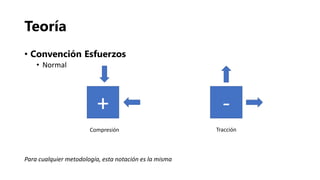
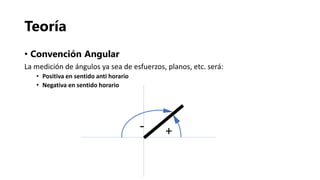
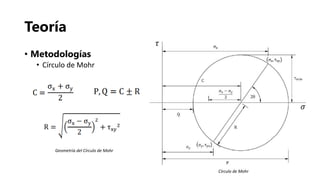
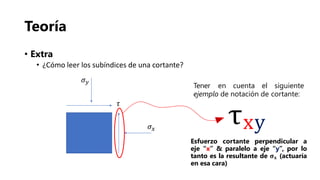
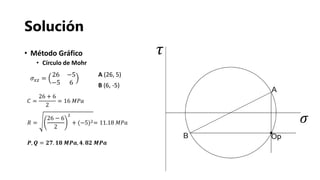
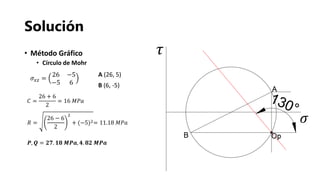
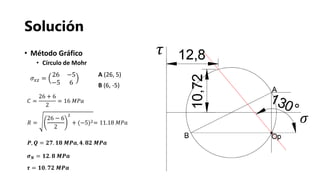
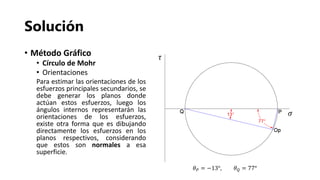
El documento presenta los fundamentos de la geomecánica bidimensional. Explica conceptos como esfuerzos normales, cortantes y principales, así como las convenciones y metodologías para su determinación, incluyendo el análisis analítico, matricial y gráfico usando el círculo de Mohr. Finalmente, propone ejercicios prácticos para aplicar los conocimientos.

1. Mecánica de Rocas I
Fundamentos de Geomecánica
Ayudantía: “Esfuerzos 2D”
Profesor: Juan Jarufe
Preparado por: Ivo Fritzler
1° Semestre 2018

2. Contenido
• Idea General
• Teoría
• Esfuerzos
• Convención de esfuerzos
• Convención angular
• Metodologías
• Analítico
• Matricial
• Tensor Bidimensional
• Gráfico
• Círculo de Mohr
• Ejercicios
• Referencias

3. Idea General
- Primer acercamiento al concepto de esfuerzo.
- Representar el estado tensional de manera
bidimensional para caracterizar ensayos de
roca, algún sector de un macizo rocoso o una
estructura mayor (falla).
- Conocer las metodologías existentes para la
determinación de estos (Analítica, Gráfica y
Matricial)
- Comprender las convenciones propuestas por
las tres metodologías, para evitar confusiones
en el trayecto del curso.
𝝈 𝑵
𝝉
𝑷
𝑸
Estado tensional en probeta de roca
Estado tensional en estructura mayor (falla)
Estado tensional in situ en macizo rocoso

4. Teoría
• Esfuerzos
“Carga distribuida en unidad de área”
• Esfuerzo Normal
• Esfuerzo Cortante
• Esfuerzos Principales
𝜎 𝑁 =
𝑃
𝐴
𝜏 =
𝑉
2𝐴
P corresponde a una carga perpendicular
a un área A.
V corresponde a una carga paralela a una
sección transversal A en la cual genera corte
𝜎1, 𝜎2, 𝜎3, 𝑃, 𝑄
𝜎1,2,3: Esfuerzos Principales considerando sistema 3D
P, Q: Esfuerzos Principales Secundarios considerando sistema 2D

5. Teoría
• Convención Esfuerzos
• Normal
+ -
Compresión Tracción
Para cualquier metodología, esta notación es la misma

6. Teoría
• Convención Esfuerzos
• Cortante
+
-
-
+
Cortante anti horario positiva
Cortante horario negativa
Aplica para:
• Metodología Gráfica
• Círculo de Mohr
Cortante anti horario negativa
Cortante horario positiva
Aplica para:
• Metodología Analítica
• Metodología Matricial
• Tensor 2D

7. Teoría
• Convención Angular
La medición de ángulos ya sea de esfuerzos, planos, etc. será:
• Positiva en sentido anti horario
• Negativa en sentido horario
+-

8. Teoría
• Metodologías
• Analítico
Si deseo rotar esfuerzos a un plano particular o obtener esfuerzos cartesianos a
partir de esfuerzos distintos de x,y,z.
Si deseo obtener la magnitud de esfuerzos principales secundarios (P,Q)
y la orientación de estos en el plano 2D correspondiente

9. Teoría
• Metodologías
• Matricial
𝜎𝑥𝑦 =
𝜎𝑥 𝜏 𝑥𝑦
𝜏 𝑦𝑥 𝜎 𝑦
𝐿 =
cos 𝜃 − sin 𝜃
sin 𝜃 cos 𝜃
𝜎𝑥´𝑦´ = 𝐿 𝑇 ∙ 𝜎𝑥𝑦 ∙ 𝐿
Donde:
𝜎 𝑥𝑦: Tensor inicial
𝐿, 𝐿 𝑇: Matrices de cosenos directores sin trasponer y traspuesta respectivamente
𝜃: Ángulo de inclinación o beta del azimut, dependerá de la dimensión 2D analizada
𝜎 𝑥´𝑦´: Tensor resultante de la nueva orientación evaluada

10. Teoría
• Metodologías
• Círculo de Mohr
Geometría del Círculo de Mohr
Círculo de Mohr

11. Teoría
• Metodologías
• Círculo de Mohr
• Teoría del Polo
Permite evaluar algún plano desconocido
de un elemento, a partir de la
intersección entre dos planos conocidos
del mismo elemento, esta intersección se
denomina Polo.
Por evaluar entiéndase como determinar
el estado tensional y orientaciones de
esfuerzos que lo componen.

12. Teoría
• Extra
• ¿Cómo leer los subíndices de una cortante?
Tener en cuenta el siguiente
ejemplo de notación de cortante:
τxy
Esfuerzo cortante perpendicular a
eje “x” & paralelo a eje “y”, por lo
tanto es la resultante de 𝛔 𝐱 (actuaría
en esa cara)
𝜎 𝑦
𝜎𝑥
𝜏

13. Ejercicio
En un sector, se ha realizado un análisis del estado tensional presente, mediante celdas triaxiales,
obteniendo la siguiente información:
Además, se detectó una falla en el sector con orientación NS/50E.
Se solicita:
Determinar estado tensional en falla y esfuerzos principales secundarios (magnitud y orientación)
para ese plano, mediante las siguientes metodologías:
✓ Analítico
✓ Matricial
✓ Gráfico
𝜎 𝑥 𝜏 𝑥𝑦 𝜏 𝑥𝑧
𝜏 𝑦𝑧 𝜎 𝑦 𝜏 𝑦𝑧
𝜏 𝑧𝑥 𝜏 𝑧𝑦 𝜎𝑧
=
26 3 −5
3 13 −4
−5 −4 6

14. W E
Solución
• Desglosando información que necesitamos para
una falla NS/50E
• Obtención de estado tensional
• Método analítico
𝜎𝑥𝑧 =
26 −5
−5 6
50°
𝝈 𝑵 = 𝟏𝟒. 𝟑𝟑 𝑴𝑷𝒂
𝝉 = −𝟏𝟏. 𝟎𝟓 𝑴𝑷𝒂
𝜽 = 𝟒𝟎°
𝑷 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝜽 𝑷 = −𝟏𝟐. 𝟔𝟒 °
𝑸 = 𝟒. 𝟖𝟐 𝑴𝑷𝒂, 𝜽 𝑸 = 𝟕𝟕. 𝟑𝟔°

15. Solución
• Método Matricial
𝐿 =
0.8090 −0.5877
0.5877 0.8090
𝜎𝑥´𝑦´ =
0.8090 0.5877
−0.5877 0.8090
∙
26 −5
−5 6
∙
0.8090 −0.5877
0.5877 0.8090
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜽 = 𝟒𝟎° 𝐿 𝑇
=
0.8090 0.5877
−0.5877 0.8090
𝜎𝑥´𝑦´ =
14.33 −11.05
−11.05 17.66
𝝈 𝑵 = 𝟏𝟒. 𝟑𝟑 𝑴𝑷𝒂
𝝉 = −𝟏𝟏. 𝟎𝟓 𝑴𝑷𝒂
𝜎𝑥´𝑦´ =
14.33 − λ −11.05
−11.05 17.66 − λ
λ1 = 27.17, λ2 = 4.82
𝑷 = 𝟐𝟕. 𝟏𝟕 𝑴𝑷𝒂
𝑸 = 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜽 𝑷 = −𝟏𝟐. 𝟔𝟒 °
𝜽 𝒒 = 𝟕𝟕. 𝟑𝟔°

16. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

17. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

18. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

19. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

20. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

21. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝜏
𝜎
A (26, 5)
B (6, -5)

22. Solución
• Método Gráfico
• Círculo de Mohr
𝐶 =
26 + 6
2
= 16 𝑀𝑃𝑎
𝑅 =
26 − 6
2
2
+ (−5)2= 11.18 𝑀𝑃𝑎
𝑷, 𝑸 = 𝟐𝟕. 𝟏𝟖 𝑴𝑷𝒂, 𝟒. 𝟖𝟐 𝑴𝑷𝒂
𝜎 𝑥𝑧 =
26 −5
−5 6
𝝈 𝑵 = 𝟏𝟐. 𝟖 𝑴𝑷𝒂
𝝉 = 𝟏𝟎. 𝟕𝟐 𝑴𝑷𝒂
𝜏
𝜎
A (26, 5)
B (6, -5)

23. Solución
• Método Gráfico
• Círculo de Mohr
• Orientaciones
Para estimar las orientaciones de los
esfuerzos principales secundarios, se
debe generar los planos donde
actúan estos esfuerzos, luego los
ángulos internos representarán las
orientaciones de los esfuerzos,
existe otra forma que es dibujando
directamente los esfuerzos en los
planos respectivos, considerando
que estos son normales a esa
superficie.
𝜃 𝑃 = −13°, 𝜃 𝑄 = 77°
𝜏
𝜎

24. Ejercicio Propuesto
La figura que se presenta a continuación, corresponde a la
representación de un pozo de agua vertical, afectado por esfuerzos
combinados en sus contornos.
Se tiene la siguiente información del estado tensional
Se solicita determinar por la metodología que usted estime
conveniente.
a. Esfuerzos principales y orientación
b. Esfuerzos combinados (normal y cortante) NS y EW con
orientación de esfuerzos normales
c. Suponga una falla N35W presente en la excavación
propuesta, determine su estado tensional con orientación de
la normal y cortante
𝜎 𝑥´ (MPa) 𝜎 𝑦´ (MPa) 𝜏 𝑦´𝑥´ (MPa)
13 21 4

25. Solución
a.Q=11.35 MPa, orientación 143°, P=22.65 MPa, orientación 53°
b. NS 18.48 MPa, 5.45 MPa, orientación 90°, EW 15.53 MPa, -5.45 MPa,
orientación 0°
c. Magnitud normal: 21.62 MPa, cortante: 3.25 MPa, Orientación normal 125°,
cortante 35°
* El ángulo de orientación de los esfuerzos propuestos en las respuestas puede tener otro valor (el
suplemento de los ángulos propuestos) con otro sentido (medición horaria - negativo) *

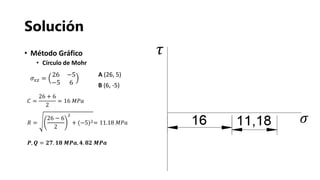
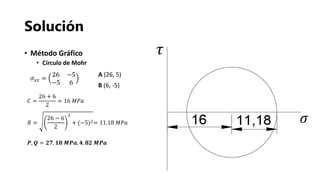
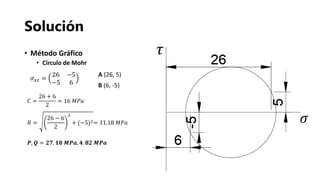
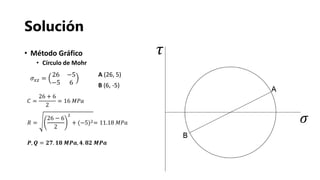
26. Referencias
• Fritzler, I. (2016): Ayudantía 0: Círculo de Mohr. Mecánica de Rocas I. Universidad de
Santiago de Chile, Santiago, Chile.
• Jarufe, J. (2016): Unidad II: Esfuerzos [Material de Clase]. Fundamentos de Geomecánica.
Universidad de Santiago de Chile, Santiago, Chile.
• Yelicich, V. (2016): Ayudantía: Círculo de Mohr. Mecánica de Rocas I. Universidad de
Santiago de Chile, Región Metropolitana, Santiago.