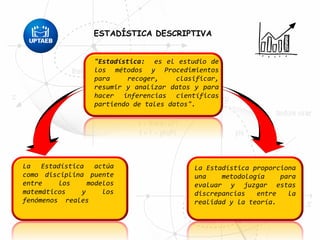
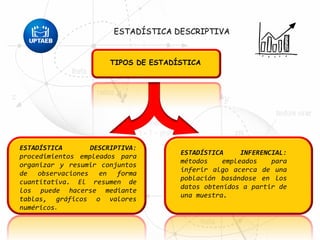
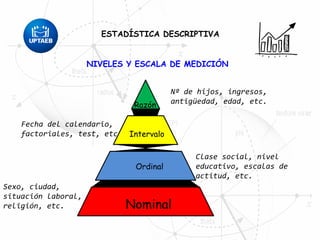
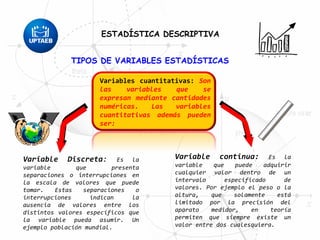
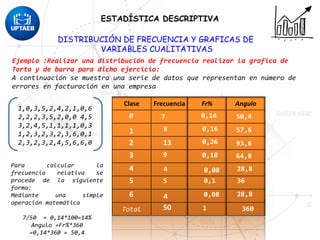
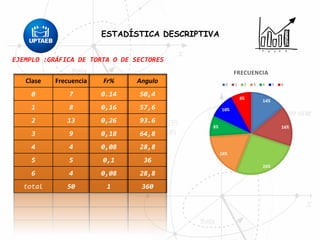
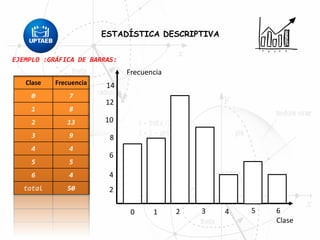
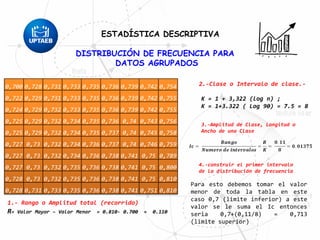
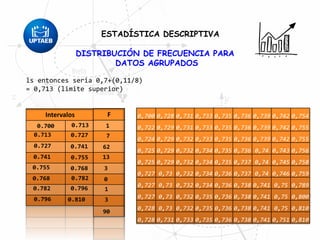
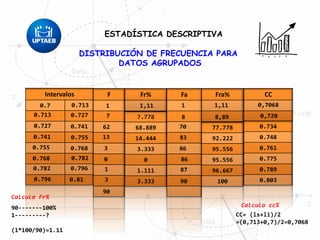
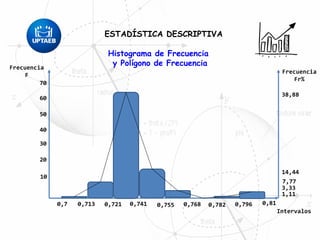
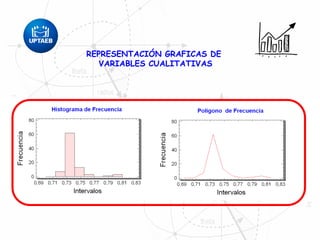
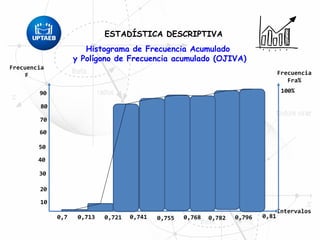
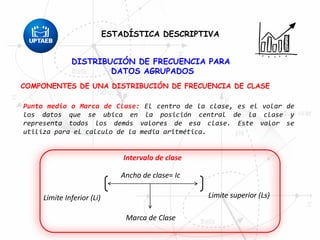
El documento trata sobre conceptos básicos de estadística descriptiva. Explica que la estadística es el estudio de métodos para recopilar, clasificar, resumir y analizar datos para hacer inferencias a partir de ellos. También distingue entre estadística descriptiva, que se usa para organizar y resumir datos, e inferencial, que se usa para inferir características de una población a partir de una muestra. Finalmente, introduce conceptos como variables, niveles de medición y distribución de frecuencias.