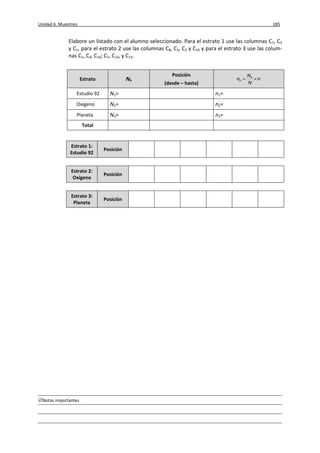
El documento abarca los conceptos fundamentales de estadística descriptiva, incluyendo definiciones de población, muestra, y clasificación de variables. Se presentan métodos de organización, presentación y análisis de datos, así como la distinción entre estadísticas descriptivas e inferenciales. Además, se discuten escalas de medición y se proveen ejemplos específicos para ilustrar cómo recopilar y interpretar datos.










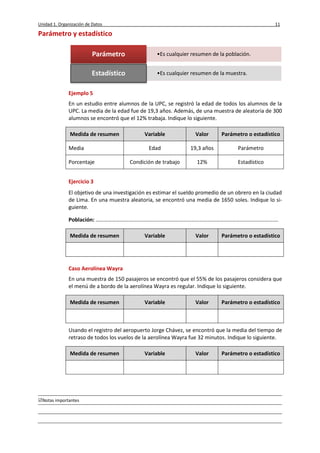


















![Unidad 1. Organización de Datos 31
Notas importantes
Ejemplo 8
El jefe de la Oficina de Rentas de una Municipalidad ha realizado un estudio sobre los
impuestos que pagan los vecinos del distrito. La tabla muestra los pagos de impuestos,
en soles, en el 2014 de 48 viviendas elegidas al azar.
145,1 216,3 252,5 303,6 196,9 234,8 265,2 317,2 206,5 242,9 289,1 331,7
151,0 225,9 257,1 305,8 202,6 238,4 271,0 320,2 208,0 244,0 291,0 344,6
159,0 227,1 259,2 315,4 204,9 239,9 286,7 324,8 208,0 247,7 291,9 346,7
195,6 231,2 262,5 315,5 206,1 241,1 288,1 331,1 209,3 249,5 294,5 351,1
Elabore la tabla de frecuencias para la variable: pago por impuestos municipales año
2014.
Solución
El rango r se calcula con:
r = valor máximo – valor mínimo = 351,1 – 145, 1 = 206
Siguiendo la regla de Sturges, el número de intervalos es:
10 101 3,322log 1 3,322log (48) 6,585 7k n
El ancho del intervalo es:
206
29,429 29,5
7
r
w
k
(Redondeo por exceso a un decimal)
Distribución de frecuencias del pago de impuestos municipales del año 2014
Pago de impuestos Marca de clase fi hi Fi Hi
[145,1 ; 174,6] 159,85 3 0,0625 3 0,0625
]174,6 ; 204,1] 189,35 3 0,0625 6 0,1250
]204,1 ; 233,6] 218,85 10 0,2084 16 0,3334
]233,6 ; 263,1] 248,35 12 0,2500 28 0,5834
]263,1 ; 292,6] 277,85 7 0,1458 35 0,7292
]292,6 ; 322,1] 307,35 7 0,1458 42 0,8750
]322,1 ; 351,6] 336,85 6 0,1250 48 1,0000
Total 48 1,0000](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-31-320.jpg)











![Unidad 1. Organización de Datos 45
Notas importantes
España. Distribución de días según prima de riesgo. Junio y julio del 2015
Prima de riesgo Marca de clase fi hi Fi Hi
[ 120 ; 130 ] 125 1 0,0200 1 0,0200
] 130 ; 140 ] 135 3 0,0600 4 0,0800
] 140 ; 150 ] 145 11 0,2200 15 0,3000
] 150 ; 160 ] 155 14 0,2800 29 0,5800
] 160 ; 170 ] 165 12 0,2400 41 0,8200
] 170 ; 180 ] 175 6 0,1200 47 0,9400
] 180 ; 190 ] 185 3 0,0600 50 1,0000
Fuente: Agencia de Calificación de Riesgos A.
Grafique el histograma de frecuencias relativas, el polígono de frecuencias absolutas y la
ojiva de frecuencias relativas.
20. Indique el tipo y escala de medición de las siguientes variables y su escala de medición.
Variable
Número de personas que van a ver una película
Género de una película (drama, comedia, acción, etc.)
Duración de una película
Opinión sobre la película (buena, regular, mala)
21. En el II Censo Nacional Universitario del año 2010 realizado por el INEI se preguntó a los
alumnos de todo el Perú por su tipo de universidad y su género. Los datos se muestran
en el siguiente cuadro.
Perú. Distribución de alumnos de pregrado por género y tipo de universidad. 2010
Género Pública Privada Total
Mujer 135 082 247 743 382 825
Hombre 174 093 226 052 400 145
Total 309 175 473 795 782 970
Fuente: INEI. II Censo Universitario. 2010
Interprete el valor “135 082” de la tabla.
Elabore un gráfico comparativo que permita ver la composición porcentual por género y
tipo de universidad.
Elabore un gráfico comparativo que permita ver la composición porcentual por género
según tipo de universidad.
Elabore un gráfico comparativo que permita ver la composición porcentual por tipo de
universidad según género.](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-45-320.jpg)




![50 Estadística Descriptiva 201601
Notas importantes
Datos simples y datos agrupados
Ejemplo de datos simples
10,6 14,5 17,2 12,8 13,6 11,6 11,3 13,0 13,5 10,8 13,9 14,2 15,3 14,3 14,3 14,3
11,8 16,1 16,8 18,8 14,8 14,0 16,4 14,2 16,5 12,1 13,3 12,0 14,3 14,9 15,1 14,4
Ejemplo de datos agrupados por intervalos
Empresa A. Distribución de obreros según descuentos en su planilla en el presente mes
Descuentos, en soles
Marca de
clase
fi hi Fi Hi
[204,1 ; 233,6] 218,85 16 0,2084 16 0,3334
]233,6 ; 263,1] 248,35 12 0,2500 28 0,5834
]263,1 ; 292,6] 277,85 7 0,1458 35 0,7292
]292,6 ; 322,1] 307,35 7 0,1458 42 0,8750
]322,1;351,6] 336,85 6 0,1250 48 1,0000
Total 48 1,0000
Fuente: RRHH Empresa A
Ejercicio 8
Luego de una investigación se tiene muchos datos, con ellos se puede realizar algunos
gráficos y distribuciones de frecuencias, pero ¿cómo resumir alguna característica de la
información en un solo número?
Datos simples
•Se denomina datos simples (datos no
agrupados) a los valores que no están
agrupados en distribuciones de
frecuencia.
Datos agrupados
•Se denomina datos agrupados a los
valores que están agrupados en
distribuciones de frecuencia.
Si se tienen datos simples no se construye la distribución de frecuencias
para calcular la media, la mediana o cualquier estadístico,
se prefiere el cálculo con los datos simples.](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-50-320.jpg)





























![82 Estadística Descriptiva 201601
Notas importantes
16. En una tienda, la desviación estándar de los precios de los jeans es de 20 soles, calcule la
nueva desviación estándar de los precios de los jeans si se realiza:
a. una rebaja del 6% de todos los precios,
b. una oferta y se rebaja ocho soles a cada precio.
17. El siguiente cuadro muestra la distribución de los sueldos mensuales, en soles, de los
empleados de las empresas A y B.
Distribución de empleados según salario mensual de las empresas A y B
Sueldos
Empresa A
Marca de
clase
fi Sueldos
Empresa B
Marca de
clase
fi
[1 500 – 2 500] 2 000 120 [3 000 – 3 500] 3 250 150
]2 500 – 3 500] 3 000 80 ]3 500 – 4 000] 3 750 120
]3 500 – 4 500] 4 000 77 ]4 000 – 4 500] 4 250 45
]4 500 – 5 500] 5 000 63 ]4 500 – 5 000] 4 750 55
Fuente: Empresa A Fuente: Empresa B
¿Cuál de los grupos presenta mayor variabilidad de salarios?
Si en la empresa A hay un aumento de sueldo del 6%, mientras que en la empresa B se
da un aumento de sueldo del 4% y una bonificación de 120 soles. Luego de los aumen-
tos, ¿qué grupo presenta mayor variabilidad de salarios?
18. Los siguientes datos representan las notas de la primera práctica de alumnos de Estadís-
tica Descriptiva. Calcule e interprete el percentil 25 de los siguientes datos.
Distribución de alumnos según notas de la primera práctica de Estadística Descriptiva
xi fi hi Fi Hi
12 5 0,025 5 0,025
13 46 0,230 51 0,255
14 109 0,545 160 0,800
16 40 0,200 200 1,000
Fuente: Secretaría Académica. Universidad A
19. Las notas de un curso de capacitación sobre tributación se muestran en la siguiente dis-
tribución de frecuencias.
Distribución de empleados según notas del curso de capacitación. Agosto 2015
Notas Marca de clase fi hi Fi Hi
08 – 10 9 15 0,1056 15 0,1056
10 – 12 11 48 0,3380 63 0,4437
12 – 14 13 60 0,4225 123 0,8662
14 – 16 15 12 0,0845 135 0,9507
16 – 18 17 7 0,0493 142 1,0000
Fuente: Empresa A. Gerencia de RRHH](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-82-320.jpg)



![86 Estadística Descriptiva 201601
Notas importantes
Variable Nombre del estadístico Valor del estadístico
Tendencia
central
Fruta consumida Moda Manzana, plátano y
pera
Dispersión Gasto promedio semanal
en productos naturales
Desviación estándar 5 soles
Posición Tipo de producto prefe-
rido
Percentil 70
29. El salario, en cientos de soles, de los trabajadores una empresa se presenta a continua-
ción:
13 12 13 14 15 15 15 18 23 24 24 25 25 36 42 48 60
Calcule el coeficiente de asimetría de Pearson
30. El siguiente cuadro muestra la distribución de los sueldos mensuales de los empleados de
las empresas A y B.
Distribución de empleados según de sueldos mensuales en la empresa A y B
Sueldos
Empresa A
Marca de
clase
fi
Sueldos
Empresa B
Marca de
clase
fi
[1 500 – 2 500] 2 000 45 [3 000 – 3 500] 3 250 18
]2 500 – 3 500] 3 000 148 ]3 500 – 4 000] 3 750 70
]3 500 – 4 500] 4 000 60 ]4 000 – 4 500] 4 250 70
]4 500 – 5 500] 5 000 15 ]4 500 – 5 000] 4 750 18
Fuente: Empresa A Fuente: Empresa B
Calcule la asimetría de los dos grupos. Realice una conclusión
31. Indique si son verdaderas o falsas las siguientes afirmaciones.
Afirmación Verdadero Falso
El coeficiente de variación se puede calcular en escalas de in-
tervalo y de razón
Si las unidades de los datos son minutos, la varianza se expresa
en minutos al cuadrado
El rango intercuartil se ve muy afectado por valores muy gran-
des o muy pequeños
El coeficiente de variación tiene las mismas unidades que la
varianza
32. Loy Toy es una red de librerías, con sucursales en los distritos de Santiago de Surco, San
Borja y San Luis. Se ha observado que durante los últimos meses los montos de ventas
vienen disminuyendo, por lo que el administrador desea conocer los factores que están
originando este problema y le ha encargado a su equipo de trabajo realizar una encuesta
entre sus clientes, seleccionados aleatoriamente de cada sucursal.](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-86-320.jpg)



























































![Unidad 4. Variables aleatorias 147
Notas importantes
Distribución exponencial
En variables que representan los tiempos de vida útil, tiempos de sobrevivencia, en
tiempos de ocurrencia en procesos de Poisson se suele utilizar la distribución exponen-
cial.
La variable aleatoria X tiene una distribución exponencial con parámetro β (β > 0) si su
función de densidad de probabilidad es:
0
1
xexf
x
;)(
Se denota X ~ Exp(β) y se lee que la variable aleatoria X sigue una distribución exponen-
cial con parámetro β.
La probabilidad de que la variable aleatoria X tome valores en el intervalo [c,d] es numé-
ricamente igual al área sombreada, y se calcula de la siguiente manera:
d
c
t
dtedXcP
1
1
Esperanza de X: XE
Varianza de X: 22
XV
Nótese que el parámetro β es igual a la media de la variable aleatoria.
Función de distribución acumulada de X
0;1
1
)(
0
xedtexXPxF
xt t
Se cumple que:
x
exXP
tXPkXtkXP /](https://image.slidesharecdn.com/cuadernoestadisticaupc-161212152745/85/Estadistica-Descriptiva-UPC-147-320.jpg)