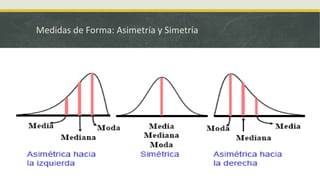
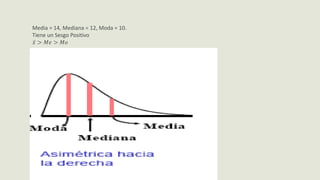
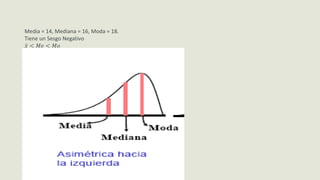
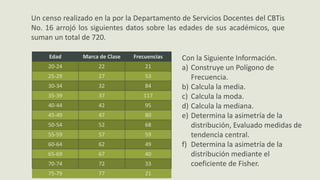
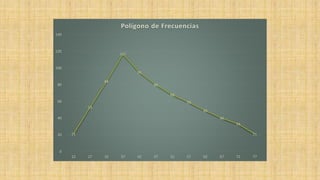
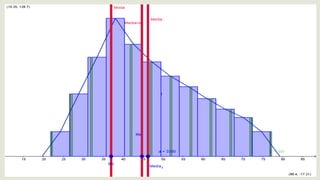
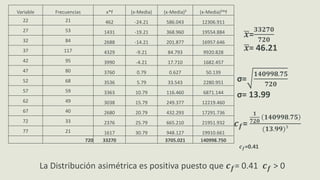
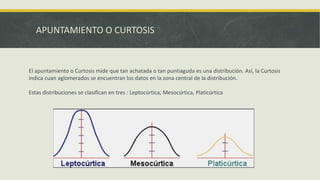
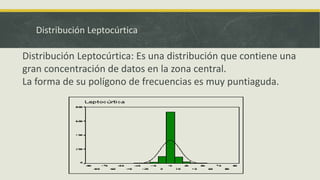
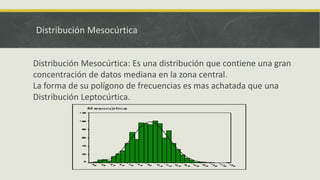
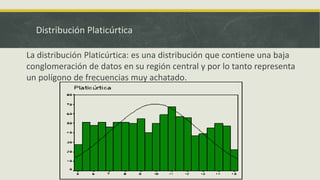
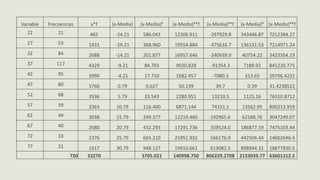
El documento presenta información sobre medidas de forma como asimetría, curtosis y coeficientes relacionados. Explica que la asimetría mide el sesgo de una distribución y puede ser positiva, negativa o simétrica dependiendo del valor del coeficiente de Pearson. También define curtosis como una medida de qué tan concentrados o dispersos están los datos alrededor de la media y clasifica las distribuciones como leptocúrtica, mesocúrtica o platicúrtica. Por último, presenta fórmulas como el coeficiente de Fisher para calcular

1. Medidas de Forma
Asimetría y Curtosis

2. Medidas de Forma Coeficiente de Pearson
Otra forma de Obtener el sesgo es mediante el Coeficiente de Karl Pearson:
Como coeficiente de una serie de datos.
Coeficiente de Pearson
𝑥 = 𝑀𝑒𝑑𝑖𝑎 𝐴𝑟𝑖𝑡𝑚𝑒𝑡𝑖𝑐𝑎
𝑀𝑑 = 𝑀𝑒 = 𝑀𝑒𝑑𝑖𝑎
𝑠 = 𝜎 = 𝐷𝑒𝑠𝑣𝑖𝑎𝑐𝑖ó𝑛 𝐸𝑠𝑡𝑎𝑛𝑑𝑎𝑟

3. Coeficiente de Pearson
El Coeficiente de Pearson varía entre -3 y 3
Si As < 0 ? la distribución será asimétrica negativa.
Si As = 0 ? la distribución será simétrica.
Si As > 0 ? la distribución será asimétrica positiva.

4. Medidas de Forma: Asimetria
Simetría
Coeficiente de Fisher
Asimetría Positiva
Asimetría Negativa

5. Medidas de Forma: Asimetría y Simetría

6. Medidas de Forma: Asimetría y Simetría
 Obtencion del Sesgo
Cualitativamente.
 Forma Simetrica:
𝑥 = 𝑀𝑒 = 𝑀𝑜
 Forma Asimetrica Negativa:
𝑥 < 𝑀𝑒 < 𝑀𝑜
 Forma Asimetríca Positiva:
𝑥 > 𝑀𝑒 > 𝑀𝑜

7. Actividad No. 1 Metodo Cualitativo
 Dados los siguientes valores de la tendencia central para cada distribución:
 Para los siguientes casos
 Media = 14, Mediana = 12, Moda = 10.
 Media = 14, Mediana = 16, Moda = 18.
 Media = 14, Mediana = 14, Moda = 14.
 Media = 14, Mediana = 17, Moda = 14.
 a) determine si ésta es simétrica. b) ¿está sesgada en forma positiva o negativa?.
Explique en cada caso. Ejemplo:

8. Media = 14, Mediana = 12, Moda = 10.
Tiene un Sesgo Positivo
𝑥 > 𝑀𝑒 > 𝑀𝑜

9. Media = 14, Mediana = 16, Moda = 18.
Tiene un Sesgo Negativo
𝑥 < 𝑀𝑒 < 𝑀𝑜

10. COEFICIENTE DE FISHER
El coeficiente de Fisher es una herramienta que sirve para
determinar la simetría o la asimetría de una distribución su
formula es:
𝑺 𝒇 =
𝟏
𝑵
(𝒙𝒊− 𝒙) 𝟑
𝑺 𝟑
Donde:
𝑆𝑓 = 𝐶𝑜𝑒𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑒 𝑑𝑒 𝐹𝑖𝑠ℎ𝑒𝑟
𝑁 = 𝑁𝑢𝑚𝑒𝑟𝑜 𝑇𝑜𝑡𝑎𝑙 𝑑𝑒 𝐷𝑎𝑡𝑜𝑠.
𝑆 = 𝐷𝑒𝑠𝑣𝑖𝑎𝑐𝑖ó𝑛 𝐸𝑠𝑡á𝑛𝑑𝑎𝑟.

11. El coeficiente de Fisher cumple con las
siguientes características.
1. Si 𝑺 𝒇 = 𝟎 Significa que la distribución es
simétrica.
2. Si 𝑺 𝒇 > 𝟎 Significa que la distribución
tiene sesgo positivo.
3. Si 𝑺 𝒇 < 𝟎 Significa que la distribución
tiene sesgo negativo.

12. Un censo realizado en la por la Departamento de Servicios Docentes del CBTis
No. 16 arrojó los siguientes datos sobre las edades de sus académicos, que
suman un total de 720.
Edad Marca de Clase Frecuencias
20-24 22 21
25-29 27 53
30-34 32 84
35-39 37 117
40-44 42 95
45-49 47 80
50-54 52 68
55-59 57 59
60-64 62 49
65-69 67 40
70-74 72 33
75-79 77 21
Con la Siguiente Información.
a) Construye un Polígono de
Frecuencia.
b) Calcula la media.
c) Calcula la moda.
d) Calcula la mediana.
e) Determina la asimetría de la
distribución, Evaluado medidas de
tendencia central.
f) Determina la asimetría de la
distribución mediante el
coeficiente de Fisher.

13. 21
53
84
117
95
80
68
59
49
40
33
21
0
20
40
60
80
100
120
140
22 27 32 37 42 47 52 57 62 67 72 77
Polígono de Frecuencias

15. Variable Frecuencias x*f (x-Media) (x-Media)² (x-Media)²*f
22 21 462 -24.21 586.043 12306.911
27 53 1431 -19.21 368.960 19554.884
32 84 2688 -14.21 201.877 16957.646
37 117 4329 -9.21 84.793 9920.828
42 95 3990 -4.21 17.710 1682.457
47 80 3760 0.79 0.627 50.139
52 68 3536 5.79 33.543 2280.951
57 59 3363 10.79 116.460 6871.144
62 49 3038 15.79 249.377 12219.460
67 40 2680 20.79 432.293 17291.736
72 33 2376 25.79 665.210 21951.932
77 21 1617 30.79 948.127 19910.661
720 33270 3705.021 140998.750
𝒙=
𝟑𝟑𝟐𝟕𝟎
𝟕𝟐𝟎
𝒙= 46.21
σ=
𝟏𝟒𝟎𝟗𝟗𝟖.𝟕𝟓
𝟕𝟐𝟎
σ= 13.99
𝒄 𝒇=
𝟏
𝟕𝟐𝟎
𝟏𝟒𝟎𝟗𝟗𝟖.𝟕𝟓
(𝟏𝟑.𝟗𝟗)³
𝒄 𝒇=0.41
La Distribución asimétrica es positiva puesto que 𝒄 𝒇= 0.41 𝒄 𝒇 > 0

16. APUNTAMIENTO O CURTOSIS
El apuntamiento o Curtosis mide que tan achatada o tan puntiaguda es una distribución. Así, la Curtosis
indica cuan aglomerados se encuentran los datos en la zona central de la distribución.
Estas distribuciones se clasifican en tres : Leptocúrtica, Mesocúrtica, Platicúrtica

17. Distribución Leptocúrtica
Distribución Leptocúrtica: Es una distribución que contiene una
gran concentración de datos en la zona central.
La forma de su polígono de frecuencias es muy puntiaguda.

18. Distribución Mesocúrtica
Distribución Mesocúrtica: Es una distribución que contiene una gran
concentración de datos mediana en la zona central.
La forma de su polígono de frecuencias es mas achatada que una
Distribución Leptocúrtica.

19. Distribución Platicúrtica
La distribución Platicúrtica: es una distribución que contiene una baja
conglomeración de datos en su región central y por lo tanto representa
un polígono de frecuencias muy achatado.

20. Formula Apuntamiento de Fisher.
Para determinar el grado de achatamiento o apuntamiento de
una distribución se utiliza el coeficiente de apuntamiento de
Fisher
𝑨 𝒇
𝟏
𝒏
𝒇(𝒙 − 𝒙)⁴
𝒔⁴
Las características de este coeficiente son las siguientes.
1. Si 𝑨 𝒇 = 3 significa que la distribución es Mesocúrtica.
2. Si 𝑨 𝒇 < 3 significa que la distribución es Platicúrtica.
3. Si 𝑨 𝒇 > 3 significa que la distribución es Leptocúrtica.

21. Variable Frecuencias x*f (x-Media) (x-Media)² (x-Media)²*f (x-Media)³*f (x-Media)⁴ (x-Media)⁴*f
22 21 462 -24.21 586.043 12306.911 -297929.8 343446.87 7212384.27
27 53 1431 -19.21 368.960 19554.884 -375616.7 136131.53 7214971.24
32 84 2688 -14.21 201.877 16957.646 -240939.9 40754.22 3423354.19
37 117 4329 -9.21 84.793 9920.828 -91354.3 7189.92 841220.775
42 95 3990 -4.21 17.710 1682.457 -7080.3 313.65 29796.4232
47 80 3760 0.79 0.627 50.139 39.7 0.39 31.4238522
52 68 3536 5.79 33.543 2280.951 13210.5 1125.16 76510.8712
57 59 3363 10.79 116.460 6871.144 74151.1 13562.95 800213.919
62 49 3038 15.79 249.377 12219.460 192965.6 62188.76 3047249.07
67 40 2680 20.79 432.293 17291.736 359524.0 186877.59 7475103.44
72 33 2376 25.79 665.210 21951.932 566176.9 442504.44 14602646.4
77 21 1617 30.79 948.127 19910.661 613082.5 898944.31 18877830.5
720 33270 3705.021 140998.750 806229.2708 2133039.77 63601312.5