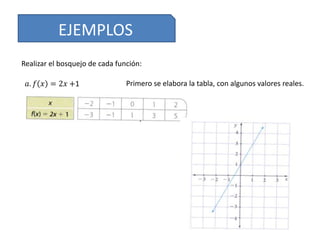
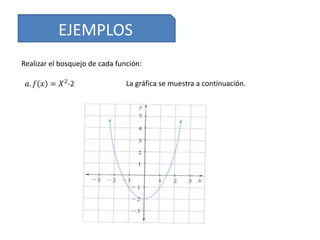
Este documento describe diferentes formas de representar funciones, incluyendo expresiones verbales, algebraicas, tablas de valores y gráficas. Explica cómo elaborar tablas de valores y bosquejar gráficas de funciones, así como un método gráfico para identificar si una gráfica representa una función verdadera mediante el trazado de líneas verticales. Proporciona ejemplos ilustrativos de estas técnicas.

1. Analiza los siguientes diagramas
sagitales

3. REPRESENTACIÓN DE
FUNCIONES
Una función se puede representar mediante la expresión verbal, la expresión
algebraica, la tabla de valores o la representación gráfica.
Forma Verbal: es la relación entre las variables que se realiza mediante una
expresión del lenguaje cotidiano.
Tabla de valores: es un arreglo de dos filas o dos columnas, en donde se escriben
los valores de la variable independiente en la primera fila o columna y sus
respectivas imágenes en la segunda.
Representación Gráfica: es la representación en el plano cartesiano de los pares
ordenados de la función.

5. EJEMPLOS
Realizar el bosquejo de cada función:
Primero se elabora la tabla, con algunos valores reales.

6. MÉTODO GRÁFICO PARA
IDENTIFICAR FUNCIONES
Para comprobar que una gráfica describe una función, se traza una línea
vertical y se verifica que esta recta corte la gráfica de la función en un solo
punto.
En el caso de que la recta corte a la gráfica en más de un punto, se afirma
que la gráfica no corresponde a una función.

7. EJEMPLOS
Realizar el bosquejo de cada función:
La gráfica se muestra a continuación.