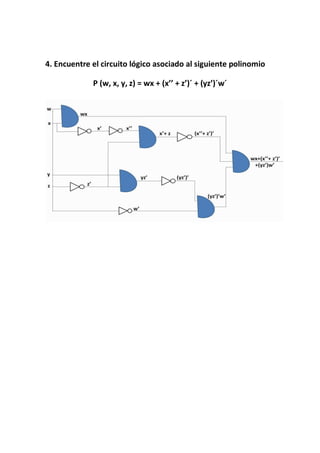
El documento presenta 4 problemas de álgebra de Boole relacionados con polinomios lógicos. El primer problema pide demostrar si dos polinomios son equivalentes. El segundo y tercer problema piden expresar polinomios dados en forma normal conjuntiva y disyuntiva respectivamente. El cuarto problema pide encontrar el circuito lógico asociado a un polinomio dado.

1. Asignatura: Estructuras Discretas II.
Profesor: Edezio Freitez
Alumno: Darwing leon C.I: 24.548.477
1. Demostrar si los siguientes polinomios son equivalentes:
P (w, x, y, z) = wx + (x’’ + z’) + (y + z’)
Q (w, x, y, z) = x + z’ + y
Justifique cada paso con la ley que esté utilizando.
R. Si P y Q son equivalentes, entonces, a traves de las leyes de Algebra de
Boole, se puede partir de la expresión P y llegar a Q .
P (w, x, y, z) = wx + (x’’ + z’) + (y + z’)
= wx + (x + z’) + (y + z’) Involución
= (wx+x) + (z’+y+z’) Asociativa
= (wx+x) + (y+z’+z’) Conmutativa
= (wx+x) + (y+z’) Idempotencia
= x + (y+z’) Absorción
= x+z’+y Conmutación
P(w,x,y,z) = Q(w,x,y,z)
Por lo tanto P y Q son Equivalentes.

2. 2. Encuentre el polinomio en Forma Normal Conjuntiva asociado
al siguiente polinomio:
P (x, y, z) = (x + y’) (x’ + z’) (y’ + z)
Justifique cada paso con la ley que esté utilizando.
Forma Normal Conjuntiva.

3. 3. Encuentre el polinomio en Forma Normal Disyuntiva asociado
al siguiente polinomio:
P (x, y, z) = (x + y’)z´
Justifique cada paso con la ley que esté utilizando.
Forma Normal Disyuntiva.

4. 4. Encuentre el circuito lógico asociado al siguiente polinomio
P (w, x, y, z) = wx + (x’’ + z’)´ + (yz’)´w´