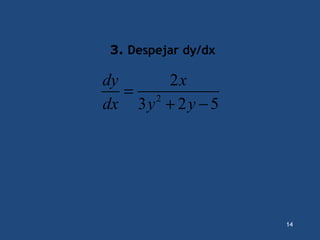Este documento explica la regla de la cadena, que permite derivar funciones compuestas. Presenta la fórmula general de la regla de la cadena y varios ejemplos de su aplicación para derivar funciones que involucran potencias, funciones trigonométricas y funciones implícitas. También cubre cómo usar la regla de la cadena para derivar expresiones que involucran ritmos o velocidades relacionadas.

1. LA REGLA DE LA
CADENA
CATEDRATICO: NICOLAS SUAREZ
UPIG 2014-I

2. LA REGLA DE LA CADENA
• Con la reglas de derivación estudiadas hasta el
momento son limitadas a expresiones sencillas.
• ¿Qué hacer cuando se tiene expresiones como la
siguiente y = (xy = (x22
− 4)− 4)53/353/3
?, resulta que es prácticamente
imposible derivarla.
• Surge la regla de la cadena que ayuda a derivar
funciones compuestas

3. Teorema. La Regla de la Cadena
• Si y = f(u)y = f(u) es una función derivable de u
• Y u = g(x)u = g(x) es una función derivable de x
Entonces:
• yy = f(g(x) es una función derivable de x y
• O su equivalente
.
dy dy du
dx du dx
=
( )( ) '( ( )) '( )
d
f g x f g x g x
dx
  = 

4. Ejemplo:
Encontrar dy/dxdy/dx para y = (x2
+ 1)3
u = x2
+ 1
u’=2x
y = u3
2
2 2
2 2
.
3 .(2 )
3( 1) (2 )
6 ( 1)
dy dy du
dx du dx
dy
u x
dx
dy
x x
dx
dy
x x
dx
=
=
= +
= +

5. Teorema. La Regla General de las
Potencias
• Si y = [u(x)]y = [u(x)]nn
donde u es una función derivable de x y n
es un número racional entonces
o su equivalente
[ ]
1
( )
ndy du
n u x
dx dx
−
=
1
[ ] 'n nd
u nu u
dx
−
=

6. Ejemplo:
Encontrar la derivada de f(x)f(x) = (3x -2x= (3x -2x22
))33
u = 3x -2x2
u’ = 3 – 4x
f(x) = u3
2
2 2
'( ) .
'( ) 3 .(3 4 )
'( ) 3(3 2 ) (3 4 )
dy du
f x
du dx
f x u x
f x x x x
=
= −
= − −

7. Ejemplo: Encontrar la derivada de
g(t)(t) = -7 / (2t – 3)= -7 / (2t – 3)22
g(t) = -7(2t – 3)-2
reescribir la función
u = 2t – 3
u’ = 2 ( )
( ) ( )
1
3
3
3
'( ) 7 ( )( )( ')
' 7 ( 2)( ) (2)
'( ) 28(2 3)
28
'( )
(2 3)
n
g t n u u
g t u
g t t
g t
t
−
−
−
= −
= − −
= −
=
−

8. Funciones Trigonométricas y la Regla
de la Cadena
[ ] ( )
[ ] ( )
[ ] ( )
2
cos '
tan sec '
sec sec tan '
d
sen u u u
dx
d
u u u
dx
d
u u u u
dx
=
=
=
[ ] ( )
[ ] ( )
[ ] ( )
2
cos '
cot csc '
csc csc tan '
d
u sen u u
dx
d
u u u
dx
d
u u u u
dx
= −
= −
= −

9. Ejemplos:
5
2
cos3y x=
2
( 3 )(6 )y sen x x= −
2
3u x=
' 6u x=
(cos ) 'y u u=
( )6y sen u x= −
2
6 ( 3 )y x sen x= −

10. Ejemplos:
5
3
( ) 4f t sen t=
3
( ) ( 4 )f t sen t=
[ ]2
'( ) 3( 4 ) 4
d
f t sen t sen t
dt
=
[ ]2
'( ) 3( 4 ) (cos 4 ) 4
d
f t sen t t t
dt
=
( ) ( )2
'( ) 3( 4 ) cos 4 4f t sen t t=
2
'( ) 12 4 cos 4f t sen t t=

11. DERIVACIÓN DE FUNCIONES
IMPLÍCITAS
• La variable y esta definida implícitamente.
– Derivar ambos lados de la ecuación respecto de x.
– Agrupar los términos en que aparezca dy/dx en el
lado izquierdo de la ecuación y los demás a la
derecha.
– Factorizar dy/dx del lado izquierdo de la ecuación
– Despejar dy/dx

12. 12
1. Derivar ambos lados de la ecuación respecto de
x
3 2 2
[ 5 ] [ 4]
d d
y y y x
dx dx
+ − − = −
[ ] [ ]3 2 2
5 4
d d d d d
y y y x
dx dx dx dx dx
     + − − = −     
2
3 2 5 2 0
dy dy dy
y y x
dx dx dx
+ − − =

13. 13
2. Agrupar los términos en que aparezca dy/dx en el
lado izquierdo de la ecuación y los demás a la
derecha
2
3 2 5 2
dy dy dy
y y x
dx dx dx
+ − =
3. Agrupar los términos en que aparezca dy/dx en el
lado izquierdo de la ecuación y los demás a la
derecha
2
[3 2 5] 2
dy
y y x
dx
+ − =

14. 14
3. Despejar dy/dx
2
2
3 2 5
dy x
dx y y
=
+ −

15. RITMOS O VELOCIDADES
RELACIONADAS
• En la mayoría de problemas sobre ritmos
relacionados, los parámetros del problema dado casi
siempre son dependientes del tiempo.
• Para proceder a derivarlos, necesariamente se debe
utilizar la regla de la cadena.

16. Ejemplo: Un obrero levanta con la ayuda de
una soga, un tablón hasta lo alto de un edificio
en construcción.
Supongamos que el otro extremo del tablón
sigue una trayectoria perpendicular a la pared
y que
el obrero mueve el tablón a razón de 0.15m/s.
¿ A qué ritmo se desliza por el suelo el
extremo
cuando está a 2.5 m de la pared?

17. Del teorema de Pitágoras se
tiene que x2
+ y2
= r2
derivamos a la expresión
como función implícita
tomando en cuenta que el
tablón no cambia de longitud.
Se tiene:
Donde:
0
dx dy
x y
dt dt
+ =

18. .x
dx y dy
v
dt x dt
= =
4.33
.(0.15)
2.5
0.26
x
x
v
mv
s
=
=