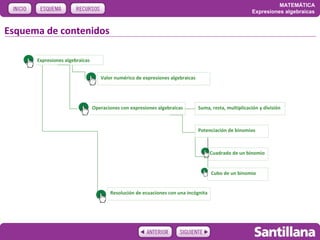
Este documento resume conceptos básicos sobre expresiones algebraicas, incluyendo: 1) cómo representan números las letras en expresiones algebraicas; 2) cómo se componen expresiones de monomios y términos; 3) cómo realizar operaciones como suma, resta, multiplicación y división con expresiones algebraicas; y 4) cómo desarrollar el cuadrado y cubo de un binomio para obtener trinomios y cuatrinomios perfectos. También resume cómo resolver ecuaciones algebraicas de una incógnita.

1. Expresiones algebraicas
ESQUEMA

2. MATEMÁTICA
Expresiones algebraicas
Esquema de contenidos
Expresiones algebraicas
Valor numérico de expresiones algebraicas
Operaciones con expresiones algebraicas Suma, resta, multiplicación y división
Potenciación de binomios
Cuadrado de un binomio
Cubo de un binomio
Resolución de ecuaciones con una incógnita

3. MATEMÁTICA
Expresiones algebraicas
Expresiones algebraicas
En las expresiones algebraicas las letras representan números y
forman la parte literal de la expresión. Podemos escribirlas de
distintas formas: 2.ab = 2ab = 2.a.b
Su valor numérico depende del valor de las letras. Por ejemplo,
si x = –1 e y = 3 resulta x3 + y3 = (–1)3 + 33 = –1 + 27 = 26
• Las expresiones algebraicas se componen de monomios o términos.
• Cada monomio tiene un coeficiente (un número) y una parte literal
(letras).
• A los términos que tiene la misma parte literal los llamamos
semejantes. Por ejemplo:
3x2 es semejante a –8x2
7c no es semejante a 5c3

4. MATEMÁTICA
Expresiones algebraicas
Operaciones con expresiones algebraicas
Para hacer cálculos con expresiones algebraicas utilizamos las propiedades
para operar con números.
Operaciones con monomios
Los monomios semejantes se pueden sumar o restar, sólo hay que sumar o restar los
coeficientes y dejar la misma parte literal.
2ab – 5ab = –3ab
Si los términos no son semejantes, la suma o la resta se deja indicada: 7x + 4y
Para multiplicar monomios calculamos el producto de los coeficientes y de la parte
literal. Si las potencias son de la misma base, sumamos los exponentes.
(–4b5c) . (–2b) = 8b6c
Para dividir monomios calculamos el cociente de los coeficientes y el de la parte literal.
Si las potencias son de la misma base, restamos los exponentes:
(5x4) : (–2x2) = –2,5x2

5. MATEMÁTICA
Expresiones algebraicas
Cuadrado de un binomio
Un binomio es la suma o resta de dos términos o
monomios. Elevándolo al cuadrado en ambos casos se
obtiene:
(a+b)2 = (a+b) . (a+b) = a2 + ab + ba + b2 = a2 + 2ab + b2
(a–b)2 = (a–b) . (a–b) = a2 – ab –ba +b2 = a2 – 2ab + b2
Al desarrollar el cuadrado de un binomio obtenemos una
expresión de tres términos llamada trinomio cuadrado
perfecto.

6. MATEMÁTICA
Expresiones algebraicas
Cubo de un binomio
Es el cubo de una suma o una resta de monomios.
(a+b)3=(a+b)(a+b)2=(a+b)
(a2+2ab+b2)=a3+2a2b+ab2+ba2+2ab2+b3=a3+3a2b+3ab2+b3
De igual forma se obtiene: (a–b)3=a3–3a2b+3ab2–b3
Hacé el desarrollo en tu carpeta.
Al desarrollar el cubo de un binomio obtenemos una
expresión de cuatro términos llamada cuatrinomio cubo
perfecto.

7. MATEMÁTICA
Expresiones algebraicas
Resolución de ecuaciones
Resolver una ecuación significa encontrar los valores que
reemplazados en el lugar de la incógnita, hacen cierta la
igualdad.
Dada 3x + 4 = 1 resulta x = –1 porque
3 . (–1) + 4 = –3 + 4 = 1
•Para resolver una ecuación hay que realizar una serie de pasos
donde conviene primero separar en términos.
•Algunas ecuaciones no tienen solución, otras tiene una única y
otras pueden tener dos, tres, etc., incluso infinitas soluciones.
Por ejemplo:
0 . x = 5 No tiene solución, porque ningún número la
verifica.
0 . x = 0 Admite infinitas soluciones.