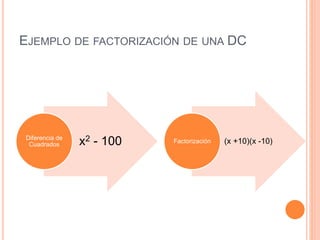
Este documento explica los conceptos básicos de la factorización de expresiones algebraicas. Define la factorización como descomponer una expresión en factores cuyo producto es igual a la expresión original. Luego, explica cómo factorizar trinomios cuadrados perfectos, trinomios de segundo grado y diferencias de cuadrados, proporcionando ejemplos para ilustrar cada tipo de factorización. Finalmente, propone ejercicios de práctica para aplicar estos conceptos.

1. FACTORIZACIÓN
Profr. Carlos Hernández Hernández
Matemáticas 9° grado

2. ¿QUÉ ES FACTORIZACIÓN?
 Es descomponer una expresión algebraica
en factores cuyo producto es igual a la
expresión propuesta.
 La factorización se considera la operación
inversa a la multiplicación, pues el propósito
de ésta última es hallar el producto de dos o
más factores; mientras que en la
factorización, se buscan los factores de un
producto dado.

3. FACTORIZACIÓN DE UN TRINOMIO CUADRADO
PERFECTO
Un Trinomio Cuadrado Perfecto es una
expresión algebraica de la forma a2+2ab+b2
.
 Para determinar si un trinomio es cuadrado
perfecto se debe:
 1.- Identificar si el primer y tercer término
son cuadrados perfectos, obteniendo la raíz
cuadrada de cada uno de los términos
 2.- El segundo término debe ser el doble
producto de la raíz cuadrada de los
términos anteriores.

4. EJEMPLO
 Si se tiene el trinomio x2 + 20x + 100
 Se identifican los dos términos probables a ser
cuadrados perfectos y se les saca la raíz cuadrada.
• x2 = x
• 100 = 10
 Verificar si el segundo término corresponde al
doble producto de las raíces de los términos
anteriores.
• 20x
 Por lo tanto x2 + 20x + 100 es un trinomio cuadrado
perfecto.

5. PROCEDIMIENTO DE LA FACTORIZACIÓN DE UN
TCP
 1.- Se obtiene la raíz cuadrada de los términos que
son cuadrados perfectos del trinomio.
 2.- Se anotan los dos términos anteriores como una
suma algebraica elevada al cuadrado.

6. EJEMPLO DE FACTORIZACIÓN DE UN TCP
TCP
• Trinomio Cuadrado Perfecto
• x2 + 10x + 25
Factorizado
• Factorizándolo
• (x + 5) (x + 5)
Factorizado
en un binomio
• Binomio al cuadrado
• (x + 5)2

7. RESUELVE LOS SIGUIENTES EJEMPLOS
x² + 18x + 81
x² + 14x + 49
x² + 6x + 9
x² + 4x + 4
x² + 8x + 16

8. FACTORIZACIÓN DE UN TRINOMIO DE
SEGUNDO GRADO
 Un Trinomio de Segundo Grado es una expresión
algebraica de la forma a2 + bx + c.
 Para determinar si un trinomio es de segundo
grado se debe:
 1.- Identificar que tenga un término cuadrado, uno
lineal y uno independiente.
 2.- Identificar si el primer término es cuadrado
obteniendo la raíz cuadrada del término.
 3.- Identificar que el término independiente no
tenga raíz cuadrada.

9. EJEMPLO
 Si se tiene el trinomio x2 - 2x - 48
 Se saca la raíz cuadrada del primer término.
• x2 = x
 Verificar si el tercer término tiene raíz cuadrada
exacta.
• √48 = 6.92
oNo tiene raíz cuadrada exacta por lo tanto es un
trinomio de segundo grado.

10. PROCEDIMIENTO DE LA FACTORIZACIÓN DE UN
TSG
 1.- Se saca la raíz cuadrada del primer término.
 2.- Encontrar parejas de números que multiplicados den el
tercer término.
 3.- Fijarse en el signo del termino independiente para deducir
como son los signos de los valores absolutos encontrados: si
es negativo son signos diferentes y si es positivo indica que
son signos iguales.
 Escoger la pareja de factores (tomando en cuenta los signos
de los factores) que reducida de el segundo término.

11. EJEMPLO DE FACTORIZACIÓN DE UN TSG
• x2 -2x -35
Trinomio de
Segundo Grado
Factorización
• (x – 7)(x +5)
• Binomio con
término
común

12. RESUELVE LOS SIGUIENTES EJEMPLOS
x2 – 3x – 40
x2 –x – 90
x2 – 2x – 63
x2 – 4x – 96
x2 - 5x - 50

13. FACTORIZACIÓN DE UNA DIFERENCIA DE
CUADRADOS
Se le llama diferencia de cuadrados a un
binomio de la forma a2 - b2
.
 Para determinar si es una diferencia de
cuadrados se debe:
 1.- Identificar que tengan raíz cuadrada los
dos términos de la expresión, si cumple con
ello es una diferencia de cuadrados.

14. EJEMPLO
 Se tiene la siguiente diferencia de cuadrados x2 - y2
Se saca la raíz cuadrada de los términos.
• x2 = x
•Y2= y
oComo tienen raíz cuadrada exacta son una
diferencia de cuadrados.

15. PROCEDIMIENTO DE LA FACTORIZACIÓN DE
UNA DC
 1.- Se saca la raíz cuadrada de los términos.
 2.- Se acomodan las raíces de los términos dentro de los
binomios (factorización).
 3.- En uno de los binomios se pone signo positivo y en el otro
signo negativo.

16. EJEMPLO DE FACTORIZACIÓN DE UNA DC
x2 - 100 Diferencia de
Cuadrados Factorización (x +10)(x -10)

17. RESUELVE LOS SIGUIENTES EJEMPLOS
x2 – 25
x2 – z2
9x2 – 16y2
64x6 – 100m4
4x2 - 49w2