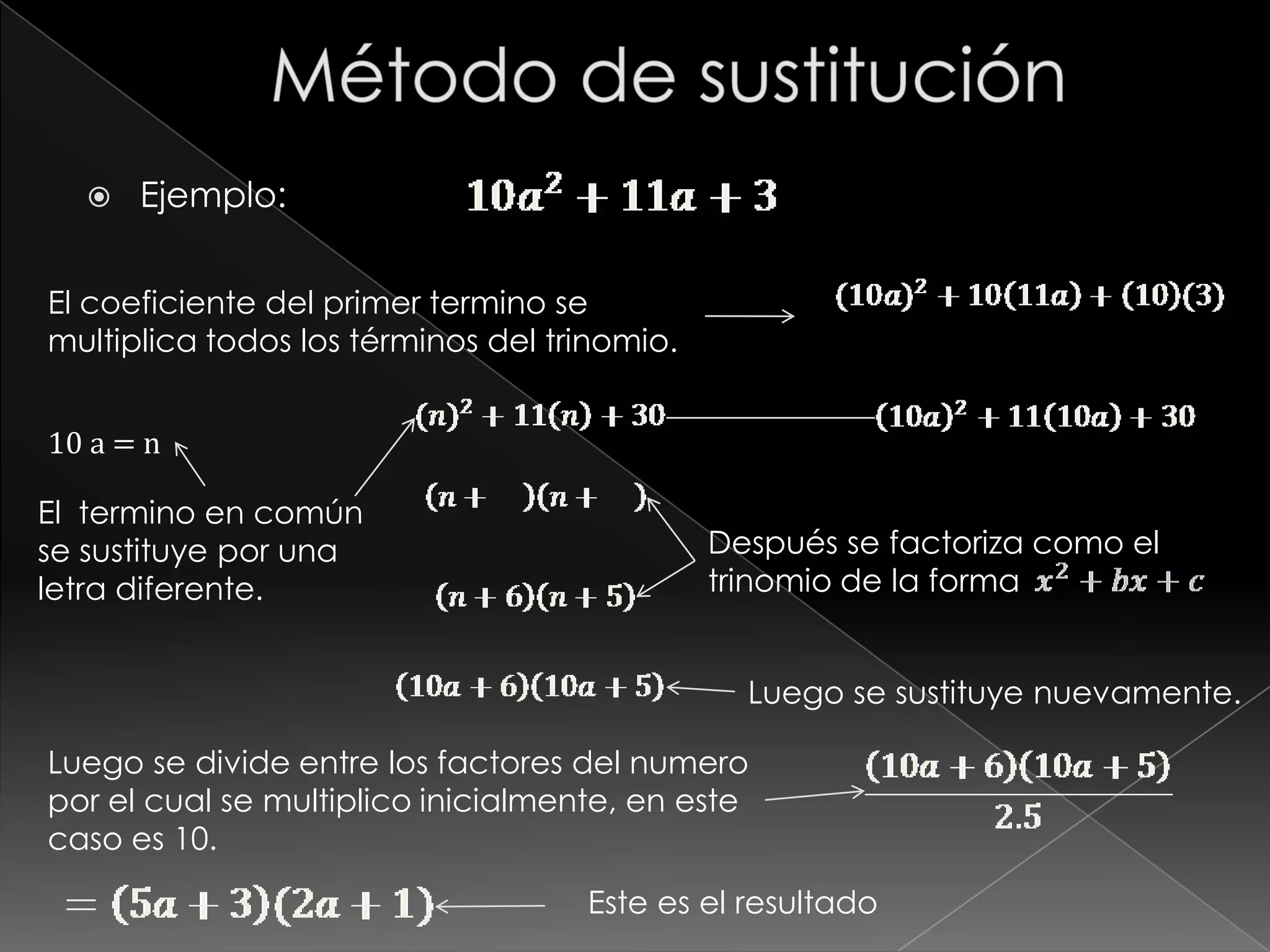
Este documento presenta 11 métodos de factorización de polinomios. Estos incluyen factor común monomio, factor común polinomio, diferencia de cuadrados perfectos, diferencia de cubos perfectos, trinomio cuadrado perfecto, y tres métodos para factorizar trinomios de la forma ax^2 + bx + c. Cada método se ilustra con un ejemplo.

1. Francisco Aguilar
Milagros Cedeño
Luis Pinilla
IXºC
Agosto 5 del 2011

2.  1. Introducción
 2.Casos de Factorización
 3. Factor común monomio
 4. Factor común polinomio
 5. Factor común por agrupación
 6. Diferencia de cuadrados perfectos
 7. Diferencia de cubos perfectos
 8. Suma de cubos Perfectos
 9. Trinomio cuadrado perfecto
 10. Trinomio de la forma
 11. Trinomio de la forma
a) Método Agrupación
b)Método Cruzado
c) Sustitución

3.  Factorización es la operación opuesta a la
multiplicación. Factorizar una expresión significa
escribirla como un producto de otras expresiones.
 Consiste en escribir una expresión como el
producto de las otras expresiones.
 El primer paso de factorización es determinar si
todos los términos del polinomio tienen un Máximo
Factor Común (MFC) y si es así factorizar por él.

4. Los casos de factorización son:
 Factor común monomio
 Factor común polinomio
 Factor común por agrupación
 Diferencia de cuadrados perfectos
 Diferencia de cubos perfectos
 Suma de cubos Perfectos
 Trinomio cuadrado perfecto
 Trinomio de la forma
 11. Trinomio de la forma
a) Método Agrupación
b)Método Cruzado
c) Sustitución

5.  Este es el caso de factorización mas
sencillo, consiste en buscar un factor
común y dividir todo por ese factor.
Ejemplo:
Es el factor
común, todo se divide
entre el.

6.  Este caso se parece al factor común
monomio pero el factor común es un
binomio.
Ejemplo:
Primero se busca =
el factor
Los demás
común, es un
términos se
polinomio = agrupan, y se
suman los términos
= semejantes.
Este es el resultado

7.  En esta factorización se necesita 4 o mas
términos y se agrupan de la mejor forma
para factorizar.
Ejemplo:
Se agrupan, los términos
cuales son mas fáciles de
factorizar por el factor
común monomio.
Se factoriza por el factor común
monomio.
Y después se factoriza por el
factor común polinomio.

8.  Esta factorización es de 2 términos lo cuales
son cuadrados perfectos. Solamente se
puede factorizar la diferencia de ellos.
Ejemplo:
Se sacan las raíces
de los términos.
Las raíces son los términos
que se utilizan en el Se multiplica, la suma y
resultado. la diferencia de las 2
raíces.

9.  La factorización de la diferencia de
cubos es el factorizar 2 términos los
cuales son cubos perfectos
Ejemplo:
Se buscan las raíces cubicas de los términos.
Las raíces se restan y ese es el primer binomio.
De las raíces que sacamos, el primer termino se eleva
al cuadrado, después se suma la multiplicación del
primero por el segundo y luego se suma el segundo
termino se eleva al cuadrado.
Se expresa la multiplicación el binomio y el
trinomio, ese es el resultado.

10.  Esta factorización es igual a la de la
diferencia de cuadrados, lo único que
cambia es el signo de la respuesta.
Ejemplo:
Se busca las raíces cubicas
Primer binomio
El primer termino se eleva al cuadrado, después
se resta la multiplicación del primero por el
segundo y luego se suma el segundo termino se
eleva al cuadrado.
Se multiplica el binomio con el
trinomio, ese es el resultado.

11.  En esta factorización se necesitan 3
términos los cuales se verifican para no
confundir que método de factorización
usar.
Ejemplo:
Se buscan las raíces
del primer y el tercer
Se multiplican las termino.
raíces por 2
Se comprueba que la
multiplicación dé el
Las raíces, se suman o se
segundo termino.
restan depende del signo
del medio y se elevan al
cuadrado

12.  Esta es una de las factorizaciones en las
que hay que pensar y tantear mas. Son
de 3 términos solamente.
Ejemplo: Se necesita que sus
factores sumados den el
segundo termino
Primero se buscan los 15 3
factores del ultimo 5 5
termino. 1 1
Se pone 2 paréntesis, en el Y se pone los
primero va la letra de la números que se
incógnita y el signo del medio, en buscaron
= anteriormente, son
el segundo va la misma letra y la
multiplicación de los 2 signos. sus signos.

13.  Este trinomio tiene 3 métodos para
factorizar.
1. Método de Agrupación
2. Método de Sustitución
3. Método Cruzado
 Este trinomio es casi igual al anterior
solamente se le agrega un coeficiente al
primer termino
 La factorización es mas larga que la
anterior, pero tiene un paso en común, la
búsqueda de factores de un numero.

14.  Ejemplo:
El termino del medio se cambia =
por 2 números que sumados den
igual a él.
Se agrupan los 2 primeros términos
= y los 2 últimos términos.
Se factoriza por el factor =
común monomio, donde se
pueda.
Luego se factoriza por el factor común
= polinomio, y este es el resultado.

15.  Ejemplo:
El primer termino se cambia por 2
números que multiplicados sean igual a
él y cada uno se pone en un paréntesis.
Al ultimo termino
se les busca sus
factores.
Los factores del ultimo termino se colocan con los
del primero, y se busca que el producto de
multiplicarlos en cruz dé el término del medio.
Cuando se encuentran esos números se
ponen alado de los factores del primero y
ese es el resultado.

16.  Ejemplo:
El coeficiente del primer termino se
multiplica todos los términos del trinomio.
10 a = n
El termino en común
se sustituye por una Después se factoriza como el
letra diferente. trinomio de la forma
Luego se sustituye nuevamente.
Luego se divide entre los factores del numero
por el cual se multiplico inicialmente, en este
caso es 10.
Este es el resultado