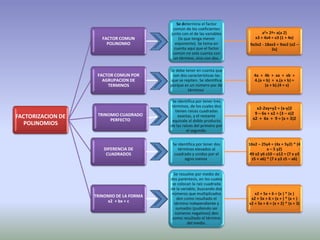
Este documento describe diferentes métodos para factorizar polinomios, incluyendo factor común, agrupación de términos, trinomio cuadrado perfecto, diferencia de cuadrados, y factorizando un trinomio de la forma x2 + bx + c.

1. FACTORIZACION DE
POLINOMIOS
FACTOR COMUN
POLINOMIO
Se determina el factor
común de los coeficientes
junto con el de las variables
(la que tenga menor
exponente). Se toma en
cuenta aquí que el factor
común no solo cuenta con
un término, sino con dos.
a2+ 2ª= a(a 2)
x3 + 4x4 = x3 (1 + 4x)
9a3x2 - 18ax3 = 9ax2 (a2 –
2x)
FACTOR COMUN POR
AGRUPACION DE
TERMINOS
Se debe tener en cuenta que
son dos características las
que se repiten. Se identifica
porque es un número par de
términos.
4a + 4b + xa + xb =
4.(a + b) + x.(a + b) =
(a + b).(4 + x)
TRINOMIO CUADRADO
PERFECTO
Se identifica por tener tres
términos, de los cuales dos
tienen raíces cuadradas
exactas, y el restante
equivale al doble producto
de las raíces del primero por
el segundo.
x2-2xy+y2 = (x-y)2
9 – 6x + x2 = (3 – x)2
x2 + 6x + 9 = (x + 3)2
DIFERENCIA DE
CUADRADOS
Se identifica por tener dos
términos elevados al
cuadrado y unidos por el
signo menos.
16x2 – 25y4 = (4x + 5y2) * (4
x – 5 y2)
49 x2 y6 z10 – a12 = (7 x y3
z5 + a6) * (7 x y3 z5 – a6)
TRINOMIO DE LA FORMA
x2 + bx + c
Se resuelve por medio de
dos paréntesis, en los cuales
se colocan la raíz cuadrada
de la variable, buscando dos
números que multiplicados
den como resultado el
término independiente y
sumados (pudiendo ser
números negativos) den
como resultado el término
del medio.
x2 + 5x + 6 = (x ) * (x )
x2 + 5x + 6 = (x + ) * (x + )
x2 + 5x + 6 = (x + 2) * (x + 3)