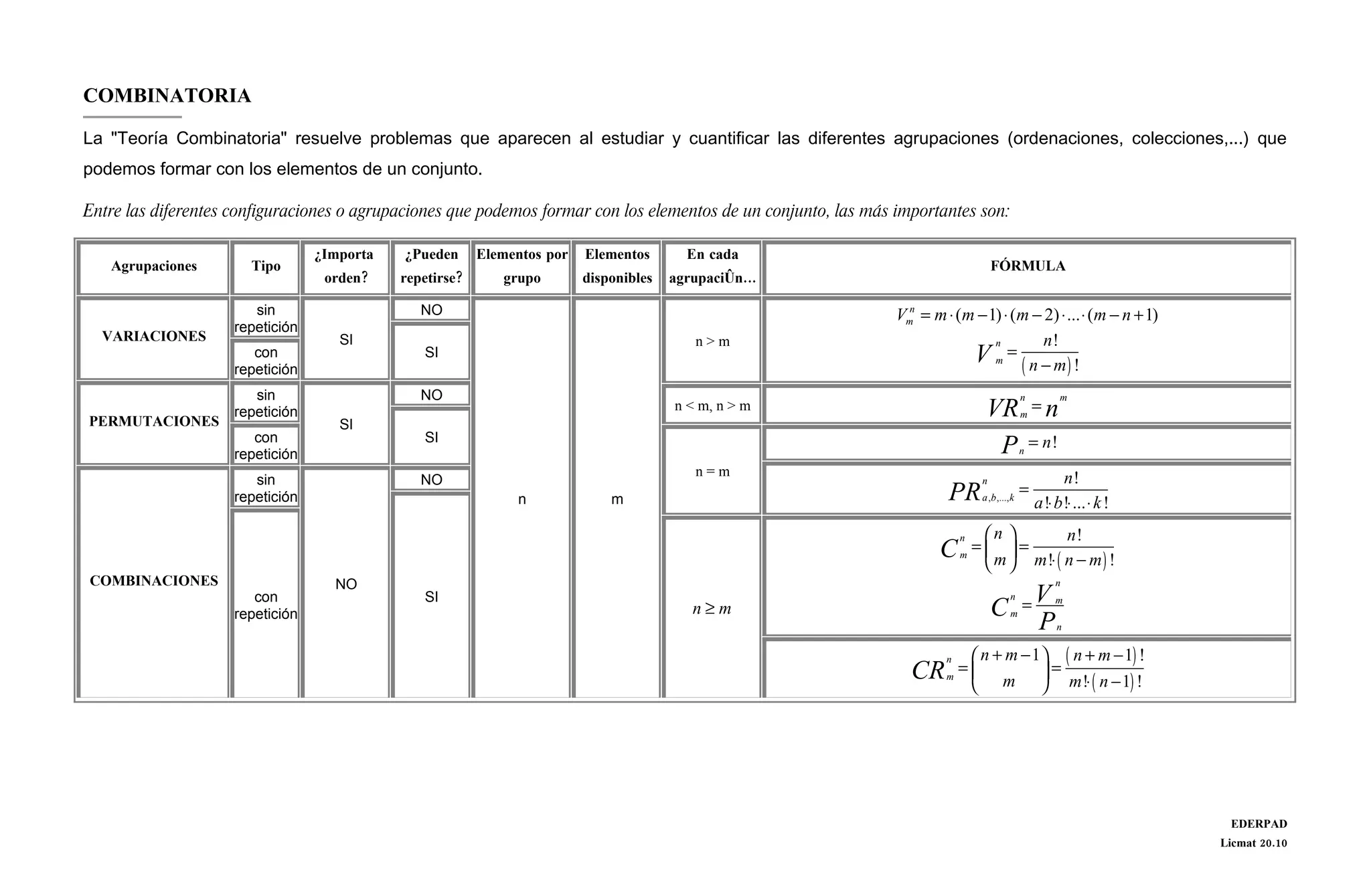
Este documento describe los diferentes tipos de agrupaciones que se pueden formar con los elementos de un conjunto, incluyendo variaciones, permutaciones, combinaciones y combinaciones con repetición. Define cada tipo de agrupación y proporciona las fórmulas matemáticas correspondientes.

1. COMBINATORIA
La "Teoría Combinatoria" resuelve problemas que aparecen al estudiar y cuantificar las diferentes agrupaciones (ordenaciones, colecciones,...) que
podemos formar con los elementos de un conjunto.
Entre las diferentes configuraciones o agrupaciones que podemos formar con los elementos de un conjunto, las más importantes son:
¿Importa ¿Pueden Elementos Elementos En cada
Agrupaciones Tipo FÓRMULA
orden? repetirse? por grupo disponibles agrupación...
sin NO Vm = m ⋅ (m − 1) ⋅ (m − 2) ⋅ ... ⋅ (m − n + 1)
n
repetición
VARIACIONES SI n>m n n!
con
repetición
SI V m = ( n − m) !
sin NO n m
PERMUTACIONES
repetición
SI
n < m, n > m VR m
=n
con SI
repetición P n
= n!
n=m n!
sin NO n
repetición n m PR a ,b ,..., k
=
a !⋅ b !⋅ ... ⋅ k !
n n  n!
C m
= =
 m  m !⋅ ( n − m ) !
COMBINACIONES NO n
con SI V n
repetición n≥m C = m
P m
n
n  n + m − 1 ( n + m − 1) !
CR m
= =
 m  m !⋅ ( n − 1) !
EDERPAD
Licmat 20.10