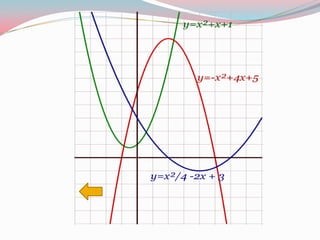
El documento proporciona una introducción a las funciones cuadráticas, incluyendo su representación analítica, raíces, y representación gráfica. Explica que una función cuadrática toma la forma f(x)=ax^2 +bx+c, y que su gráfica es una parábola. Las raíces de la función, o los valores de x para los que f(x)=0, dependen del valor del discriminante y pueden haber uno o dos valores de raíz. La función también puede escribirse de varias formas equivalentes como forma desarrollada, factor

1. CURSO: COMUNICACIÓN Y TECNOLOGÍA EDUCATIVA
FACILITADOR: Prof. Marcos Botacio
ELOY E. RICO RÍOS
Febrero 2013

2. Agradecemos la valiosa ayuda del Prof. Marcos Botacio al indicarnos
varios aportes para la elaboración de este trabajo, en lo que respecta
el manejo de estas herramientas.

4. En Matemática, una función cuadrática o función de segundo grado es
una función polinómica definida como:
ƒ( )= a ²+ +
donde a, b y c son números reales (constantes) y a es distinto de cero .
La representación gráfica en el plano cartesiano de una función
cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las
ordenadas. La parábola se abrirá hacia arriba si el signo de a es
positivo, y hacia abajo en caso contrario. El estudio de las funciones
cuadráticas tiene numerosas aplicaciones en campos muy
diversos, como por ejemplo la caída libre o el tiro parabólico. (Ver
gráficas)

5. 1. Raíces
2. Representación analítica
Forma desarrollada
Forma factorizada
Forma canónica
3. Representación gráfica
Corte con el eje x
Corte con el eje y
Extremos
4. Despedida

7. Las raíces (o ceros) de una función cuadrática, como
toda función algebraica, son los valores de x, para los
cuales ƒ )=0 . Por tratarse de un polinomio de grado
2, habrá a lo sumo 2 raíces, denotadas habitualmente
como: ₁ y ₂, dependiendo del valor del discriminante
Δ definido como :
 ²-4ac
=
Para ampliar este concepto, vamos a

8. Existen tres formas principales de escribir una función
cuadrática, aplicables según el uso que se le quiera dar
a la función: un estudio analítico de la función o de la
ecuación cuadrática, una interpretación o construcción
geométrica de la parábola, etc. Las tres formas son
equivalentes:
Forma desarrollada
Forma factorizada
Forma canónica

9. Toda función cuadrática se puede escribir en forma
factorizada en función de sus raíces como:
ƒ( )= ( - ₁)( - ₂)
Siendo ₁ y ₂ las raíces de ƒ. Si el discriminante es
igual a cero, ₁= ₂; entonces:
ƒ( )= ( - ₁)²