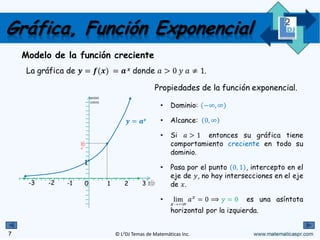
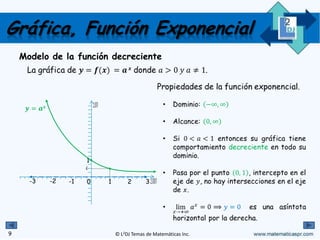
El documento cubre las funciones exponenciales y logarítmicas, incluyendo su definición, características, gráficas y cómo resolver ecuaciones exponenciales. Se explican conceptos como dominancia, rango y comportamiento creciente o decreciente de estas funciones, así como ejemplos prácticos y ejercicios para ilustrar el contenido. Adicionalmente, se proporciona la regla para resolver ecuaciones exponenciales igualando bases y exponentes.