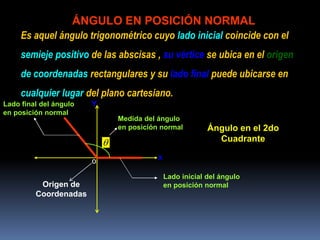
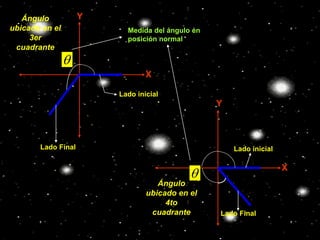
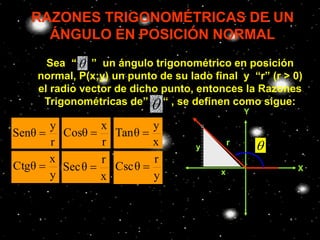
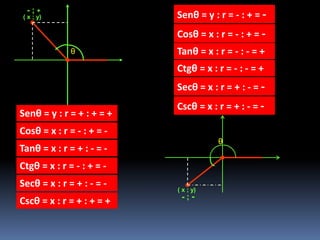
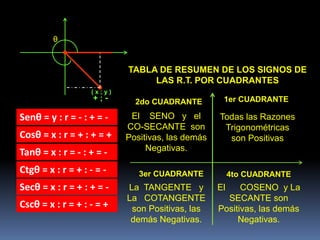
Este documento define un ángulo en posición normal como uno cuyo lado inicial coincide con el eje positivo de las abscisas, su vértice está en el origen de coordenadas y su lado final puede estar en cualquier lugar del plano cartesiano. Explica que las razones trigonométricas de un ángulo en posición normal se definen en términos de las coordenadas del punto final del lado del ángulo y su radio vector. Finalmente, resume que los signos de las razones trigonométricas dependen de los cuadrantes en los que se ubique el áng

1. Trigonometría
Moderna
ÁNGULOS EN POSICIÓN NORMAL
Y SUS
RAZONES TRIGONOMETRICAS

2. ÁNGULO EN POSICIÓN NORMAL
Es aquel ángulo trigonométrico cuyo lado inicial coincide con el
semieje positivo de las abscisas , su vértice se ubica en el origen
de coordenadas rectangulares y su lado final puede ubicarse en
cualquier lugar del plano cartesiano.
x
Y
Lado inicial del ángulo
en posición normal
Lado final del ángulo
en posición normal

Medida del ángulo
en posición normal Ángulo en el 2do
Cuadrante
o
Origen de
Coordenadas

3. Y
X
Lado inicial
Lado Final

Medida del ángulo en
posición normal
Ángulo
ubicado en el
3er
cuadrante
X
Y

Lado inicial
Lado Final
Ángulo
ubicado en el
4to
cuadrante

4. RAZONES TRIGONOMÉTRICAS DE UN
ÁNGULO EN POSICIÓN NORMAL
Sea “ ” un ángulo trigonométrico en posición
normal, P(x;y) un punto de su lado final y “r” (r > 0)
el radio vector de dicho punto, entonces la Razones
Trigonométricas de” “ , se definen como sigue:
X
Y

 yxP ;
y
x
rr
y
Senθ 
r
x
Cosθ 
x
y
Tanθ 
y
x
Ctgθ 
x
r
θSec 
y
r
θCsc 


5. Del gráfico:
x
y
 12;5

x
y
Como:
222
yxr 
Entonces:    222
125 r
13r 
Calcula todas las R.T. de 
Luego:
13
12

r
y
Sen
13
5

r
x
Cos
5
12


x
y
Tan
12
5

y
x
Ctg
5
13


x
y
Sec
12
13

y
r
Csc

6. 2) Calcula: CscθSecθ en:
-2
-1
θ
Resolución.-
Lo primero será calcular el valor del radio vector r
r
    222
r12 

Entonces: 5r;1y;2x 
CscθSecθLuego:
 y
r
x
r
  1-
5
2-
5

CscθSecθ  2
52
2
5 


 2
53
θ

7. En el gráfico:
SecφSenφ 
( 4 ; 5)
Calcula:
( -4 ; -5)
Resolución.-
Trasladamos el punto (4;5) por simetría, asiendo rotaciones de 90°.
Luego:
SecφSenφ  =
4
41
41
5



=
414
21

 =
414
21
θ

8. SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
Como las razones trignométricas dependen de dos cantidades
(abscisas, ordenadas y/o radio vector), nos percatamos que las
razones trigonométricas tienen un signo que se obtiene de la
combinación de los signos que poseen estas cantidades.
( x ; y)
+ ; +
θ
Senθ = y : r = + : + = +
Cosθ = x : r = + : + = +
Tanθ = x : r = + : + = +
Ctgθ = x : r = + : + = +
Secθ = x : r = + : + = +
Cscθ = x : r = + : + = +

9. ( x ; y)
- ; +
θ
Senθ = y : r = + : + = +
Cosθ = x : r = - : + = -
Tanθ = x : r = + : - = -
Ctgθ = x : r = - : + = -
Secθ = x : r = + : - = -
Cscθ = x : r = + : + = +
θ
Senθ = y : r = - : + = -
Cosθ = x : r = - : + = -
Tanθ = x : r = - : - = +
Ctgθ = x : r = - : - = +
Secθ = x : r = + : - = -
Cscθ = x : r = + : - = -
( x ; y)
- ; -

10. θ
( x ; y )
+ ; -
Senθ = y : r = - : + = -
Cosθ = x : r = + : + = +
Tanθ = x : r = - : + = -
Ctgθ = x : r = + : - = -
Secθ = x : r = + : + = -
Cscθ = x : r = + : - = +
TABLA DE RESUMEN DE LOS SIGNOS DE
LAS R.T. POR CUADRANTES
1er CUADRANTE
Todas las Razones
Trigonométricas
son Positivas
2do CUADRANTE
El SENO y el
CO-SECANTE son
Positivas, las demás
Negativas.
3er CUADRANTE
La TANGENTE y
La COTANGENTE
son Positivas, las
demás Negativas.
4to CUADRANTE
El COSENO y La
SECANTE son
Positivas, las demás
Negativas.

11. ALGUNAS APLICACIONES