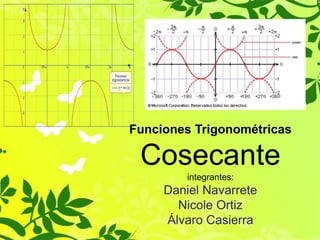
El documento describe la función cosecante. Define la cosecante como la razón trigonométrica inversa del seno. Explica que las propiedades de la cosecante se pueden deducir de las propiedades del seno y enumera algunas características clave como su dominio, recorrido, asíntotas y período. También analiza cómo la cosecante se comporta cuando el seno tiende a cero o es igual a uno.

1. Page 1
Funciones Trigonométricas
Cosecante
integrantes:
Daniel Navarrete
Nicole Ortiz
Álvaro Casierra

2. Page 2
Cosecante
La función cosecante (abreviado
como csc o cosec) es la
razón trigonométrica inversa del seno, o también
su inverso multiplicativo.
Se define la función cosecante como:
Por lo tanto, las propiedades se pueden deducir
a partir de la función seno.

3. Page 3
Las características fundamentales de
la función cosecante son las
siguientes:
1) Su dominio es R - {k·π} con k∈Z .
2) Su recorrido es R - (- 1, 1) .
3) No corta al eje X ni al eje Y.
4) Es impar, es decir, simétrica respecto al origen. cosec (- x) = - cosec
(x)
5) Tiene infinitos máximos relativos en los puntos de la forma (- π/2 + 2·k·π, -
con k∈Z .
Tiene infinitos mínimos relativos en los puntos de la forma (π/2 + 2·k·π, 1)
con k∈Z .
6) Es periódica de periodo 2π
cosec (x) = cosec (x + 2π)
7) Tiene asíntotas verticales en los puntos de la forma x =
k·π con k∈Z .
8) No está acotada

4. Page 4
Partiendo de la definición de cosecante como la inversa del seno:
Y conociendo la función seno previamente, podemos definir que para los
valores en los que el seno vale cero, la cosecante se hace infinito, si la función
seno tiende a cero desde valores negativos la cosecante tiende a: infinito
negativo.

5. Page 5
Cuando el seno del ángulo vale uno, su cosecante también vale uno.
mientras que cuando el seno tiende a cero desde valores positivos la
cosecante tiende a: infinito positivo.

6. Page 6
Tabla de valores

7. Page 7
Representación gráfica

8. Page 8
Gráfica de seno y
cosecante

9. Page 9