Este documento describe las funciones seno y coseno. Explica que la función seno asocia valores entre -1 y 1 a ángulos medidos en radianes, es periódica con período 2π, y se anula cada kπ radianes. La función coseno también asocia valores entre -1 y 1 a ángulos en radianes, es simétrica y periódica con período 2π. Ambas funciones son gráficadas para ilustrar sus propiedades.

1. FUNCION SENO-COSENO
TRABAJO PRESENTADO POR: ANDRES FELIIPE TOBAR
PROFESOR: JORGE FIGUEROA
INSTITUCION EDUCATIVA MUNICIPAL CIUDAD DE PASTO

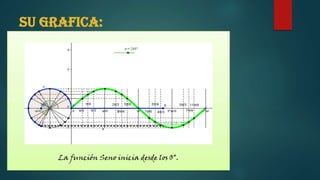
2. FUNCION SENO
En esta función se considera que el ángulo siempre debe expresarse en radianes. Para representar
dicha función, tan sólo deben trasladarse los valores del seno obtenidos a partir de la circunferencia
unitaria a la gráfica de la función. A continuación miraremos las características resultantes de esta
función.
• Su dominio contiene a todos los reales. En cambio, su imagen es el intervalo [-1,1], ya que el seno de un
ángulo siempre se encuentra entre estos valores.
•Esta función se repite exactamente igual cada 2π; es decir, los valores de la función en el intervalo del
dominio [0,2π) son suficientes para conocer la función en cualquier punto. Se dice, en este caso, que la
función es periódica, de período 2π.
• La función se anula en los valores x iguales a kπ, siendo k un número entero.
• La función alcanza sus extremos máximos, es decir, los valores mayores de la y, cuando el seno del
ángulo es 1, es decir, cuando la x es π2+2kπ, siendo k un número entero cualquiera. Sus
extremos mínimos, es decir, los valores menores de la y (cuando el seno es -1), se encuentran cuando
la x es 3π2+2kπ, siendo k cualquier número entero.

3. SU GRAFICA:

4. Características:
F(X) – SEN (x) Y: VARIABLE DEPEN
Y-SEN(x) X: VARIABLE INDEPENDIENTE
DOMINIO: TODOS LOS REALES
RANGO: (-1,1)
________________________________________________________________________________________
CUADRANTES
PRIMERO: (0. 𝜋/2) – (0.90)
SEGUNDO: (𝜋/2, 𝜋) – (90 – 180)
TERCERO: (𝜋,3𝜋/2) – (180, 270)
CUARTO: (3𝜋/ 2,2 𝜋) – (270,360)
PERIODO:
(0.2𝜋)

5. INTERVALOS DE CRECIMIENTO
(0, 𝜋/2)
(3𝜋/2.2, 𝜋)
INTERVALOS DE DECRECIMIENTO:
(𝜋/2.3𝜋/2)
PUNTO MAXIMO: X-𝜋/2
PUNTO MINIMO: 3𝜋/2

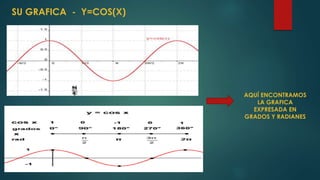
6. FUNCION COSENO
La función coseno asocia a cada número real, x, el valor del coseno del ángulo cuya medida en radianes es x.
PROPIEDADES:
- Dominio: D(f)= R
- Recorrido: R(f)= [-1,1]
- Puntos de corte con los ejes:
-Con el eje x: (/2,0), el corte se repite cada .
-Con el eje y: (0,1)
-Simetría: par; ya que, cos(-x)=cos(x).
-Asíntotas: carece de asíntotas.
--Es creciente en el intervalo: [,2].
-Es decreciente en el intervalo: [0, ].
-Acotación: la función está acotada(1< cos x <(-1)) ya que lo está superior e inferiormente:
-1 es cota superior; ya que, 1 < cos x
-(-1) es cota inferior; ya que, -1> cos x
-El valor máximo es 1 y se alcanza cada 2 veces
-El valor mínimo es (-1) y se alcanza cada 2 veces
-La función es continua en todo su dominio.
-Es periódica, su periodo es 2.

7. SU GRAFICA - Y=COS(X)
AQUÍ ENCONTRAMOS
LA GRAFICA
EXPRESADA EN
GRADOS Y RADIANES

8. EN ESTE VIDEO
ENCONTRAREMOS LA
EXPLICACION DETALLADA DE
ESTA FUNCION CON SUS
PROPIEDADES Y SU GRAFICA
EN TRIGONOMETRIA EL COSENO DE UN ANGULO EN UN TRIANGULO
RECTANGULO SE DEFINE COMO LA RAZON ENTRE EL CATETO ADYACENTE Y LA
HIPOTENUSA.
DE DEFINE POR : Cosa=b/c
Otro modo de obtener el coseno de un ángulo consiste en representar éste
sobre la circunferencia goniométrica, es decir, la circunferencia
unitaria centrada en el origen. En este caso el valor del coseno coincide con
la abscisa del punto de intersección del ángulo con la circunferencia.

9. CARACTERISTICAS:
F(X) - COS(X) Y: VARIABLE DEPENDIENTE
Y-COS(x) X: VARIABLE INDEPENDIENTE
_____________________________________________________________
DOMINIO: TODOS LOS REALES
RANGO: (-1,1)
__________________________________________________
CUADRANTES:
PRIMERO: (1/𝜋/2) – (0.90)
SEGUNDO: (𝜋/2𝜋) – (90 180)
TERCERO: (𝜋.3𝜋/2) – (180,270)
CUARTO: (3𝜋/2,2𝜋) – (270,360)
_________________________________
PERIODO: Y(1) Y(6,2) (-𝜋/2, 𝜋)

10. INTERVALOS DE CRECIMIENTO:
(3,7,4,7) (4,7 6.2)
INTERVALOS DE DECRECIMIENO:
(𝜋,2𝜋) (𝜋,3𝜋/2)
CEROS DE LA FUNCION:
(𝜋,3𝜋/2)


11. PUNTO MAXIMO:
(0.2𝜋)
PUNTO MINIMO:
(𝜋)

12. GRACIAS