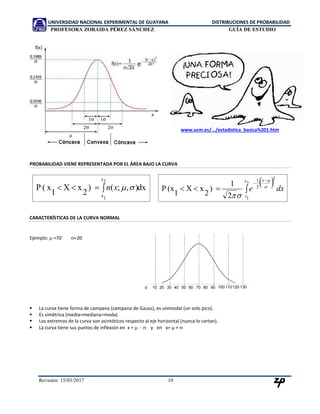
El documento es una guía de estudio sobre distribuciones de probabilidad, que abarca conceptos de variables aleatorias discretas y continuas, funciones de probabilidad, y modelos de probabilidad como Bernoulli y binomial. Se explican métodos para calcular probabilidades, valor esperado y varianza, además de ofrecer ejemplos prácticos. La guía se dirige a estudiantes de estadística en la Universidad Nacional Experimental de Guayana.