El documento explica conceptos lógicos como implicaciones lógicas, argumentos válidos e inválidos, y formas de argumento válidas como modus ponens, modus tollens, simplificación, adición y eliminación. Proporciona ejemplos para ilustrar cada concepto y cómo analizar la validez de argumentos usando tablas de verdad.

1. Se dice que la proposición P implica lógicamente la proposición Q, y se
escribe P⇒Q, Si Q es verdad cuando P es verdad.
Un p→q también es verdadero si p es falsa pero no es
nuestro caso ya que sabemos que p es verdadero, así
que no hay que analizar esa opción
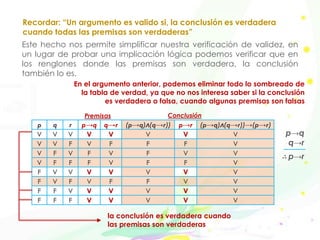
• Si (p→q)^p es verdadera, al ser una
conjunción, tanto p→q como p son
verdaderas. Si observamos la tabla de
verdad del condicional vemos que
donde eso ocurre se tiene que q es
verdadera
Implicaciones Lógicas
Por Ejemplo.
La implicación lógica [(p→q)^p]⇒q se conoce como modus ponens o
razonamiento directo, veamos que cuando P: [(p→q)^p] es verdad Q: q
es verdad

2. • Si p→(q→r) ^ q es verdadera, tenemos que p→(q→r) es
verdadera y que q es verdadera
• Si sabemos que p→(q→r) es verdadera, pueden darse dos
caso para p:
Caso 1: Que p sea verdadera, luego q→r debe ser verdadera
y ya que sabemos que q es verdadera, se tiene que r debe
ser verdadera.
Así, si p es verdadera r tambien, por lo que p→r es verdadera
Caso 2: Que p sea falsa, Si p es falsa no importa el valor de
verdad de r, p→r es verdadera.
IMPORTANTE:
En el primer caso se usa el hecho de que “un verdadero implica un
verdadero”. Si se sabe que el condicional es verdadero y la hipotesis es
cierta, la conclusión debe ser cierta
En el segundo caso se uso el hecho que “un falso implica cualquier cosa”.
Si se sabe que el condicional es verdadero y la hipotesis es falsa, la
conclusión puede ser verdadera o falsa.
Otro Ejemplo.
Probaremos la implicación lógica [ p→(q→r) ^ q ] ⇒ p→r

3. P implica lógicamente Q, P⇒Q, si, y solo si la proposición condicional
P→Q es una tautología.
Analizar una implicación lógica puede ser algo un poco complicado,
pero eso si, interesante, otra forma de probar una implicación se
desprende del siguiente teorema:
p q r p→q q→r (p→q)ʌ(q→r)) p→r ((p→q)ʌ(q→r))→(p→r)
V V V V V V V V
V V F V F F F V
V F V F V F V V
V F F F V F F V
F V V V V V V V
F V F V F F V V
F F V V V V V V
F F F V V V V V
Por Ejemplo.
La implicación lógica (p→q)ʌ(q→r))⇒(p→r) se conoce como
transitividad, veamos que (p→q)ʌ(q→r)) →(p→r) es una tautología
El análisis de si Q es verdad cuando P es verdad, en esta implicación es un
poco mas extenso que los ejemplos anteriores, pero ese análisis se puede
observar en la tabla de verdad

4. Argumentos
Un argumento es una lista de proposiciones llamadas premisas seguida
por una proposición llamada la conclusión.
Ejemplo1: “Si apruebo la clase, me darán un premio, y estoy seguro
que aprobare, así que tengo ganado ese premio .”
Si definimos, p: “aprobar la clase”, y q: “recibir un premio”
Premisas:
• p→q: “Si apruebo la clase entonces
me darán un premio”
• p: “aprobare la clase”
Conclusión:
• q: “recibir el premio”
Podemos escribir un argumento de esta forma:
-Si apruebo la clase, me darán un premio
-Estoy seguro que aprobare
Por tanto, Me ganare el premio
p→q
p
∴ q
Premisas
Conclusión

5. Ejemplo2: “Si llueve, me da gripe, y tengo gripe, así que llovió.”
Si definimos, p: “llueve”, y q: “tengo gripe”
Podemos escribir un argumento de esta forma:
-Si llueve entonces me da gripe
-Tengo gripe
Por tanto, llovio
p→q
q
∴ p
Premisas
Conclusión
Ejemplo3: “Cuando llueve se hace lodo y cuando la tierra esta lodosa
mis zapatos se ensucian. Así que, cuando llueve mis zapatos se
ensucian.”
Sea p: “llueve”, q: “hay lodo” y r: “mis zapatos se ensucian”
Podemos escribir un argumento de esta forma:
p→q
q→r
∴ p→r

6. Validez de un argumento
Ejemplo1: “Si apruebo la clase, me darán un premio, y estoy seguro
que aprobare, así que tengo ganado ese premio .”
El argumento es de la forma:
p→q
p
∴ q
Decimos que un argumento es válido si la conjunción de sus premisas
implica lógicamente a su conclusión. (p1^ p2 ^…^pn)⇒ C
En otras palabras: “Un argumento es valido si, la conclusión es
verdadera cuando todas las premisas son verdaderas”
No garantizamos la verdad de las premisas, se garantiza que si las
premisas son ciertas la conclusión también lo será
Analicemos la validez de nuestros ejemplos
RECORDAR: P⇒Q, si, y solo si P→Q es una tautología.
De la tabla podemos ver que ((p→q)ʌp)→q es una tautología, así que
el argumento es valido
p q p→q (p→q)ʌp ((p→q)ʌp)→q
V V V V V
V F F F V
F V V F V
F F V F V

7. Ejemplo2: “Si llueve, me da gripe, y tengo gripe, así que llovió.”
El argumento es de la forma:
p→q
q
∴ p
De la tabla podemos ver que ((p→q)ʌq)→p no es una tautología, así
que el argumento es no valido
p q p→q (p→q)ʌq ((p→q)ʌq)→p
V V V V V
V F F F V
F V V V F
F F V F V
¿Qué significa No Valido?
Aunque las premisas sean ciertas, se puede dar el caso que la
conclusión sea falsa , en la fila remarcada se puede observar que p→q
y q (las premisas) son verdaderas pero p (la conclusión) es falsa.
Podemos analizarlo con un ejemplo:
“Puede ser que no haya llovido (conclusión p falsa) y tengas gripe
(premisa q verdadera) por que te contagio un amigo.”
Nota que el enunciado: “Si llueve me da gripe” es verdadera ya
que un falso implica un verdadero (así premisa p→q verdadera)
En lógica, una falacia es un argumento que
parece válido, pero no lo es.

8. Ejemplo3: “Cuando llueve se hace lodo y cuando la tierra esta
lodosa mis zapatos se ensucian. Así que, cuando llueve mis zapatos
se ensucian.”
El argumento es de la forma:
De la tabla podemos ver que (p→q)ʌ(q→r))→(p→r) es una tautología,
así que el argumento es valido
Si un argumento tiene demasiadas premisas
y proposiciones, probarlo de esta manera
puede ser demasiado costosa
p→q
q→r
∴ p→r
p q r p→q q→r (p→q)ʌ(q→r)) p→r (p→q)ʌ(q→r))→(p→r)
V V V V V V V V
V V F V F F F V
V F V F V F V V
V F F F V F F V
F V V V V V V V
F V F V F F V V
F F V V V V V V
F F F V V V V V

9. Recordar: “Un argumento es valido si, la conclusión es verdadera
cuando todas las premisas son verdaderas”
Este hecho nos permite simplificar nuestra verificación de validez, en
un lugar de probar una implicación lógica podemos verificar que en
los renglones donde las premisas son verdadera, la conclusión
también lo es.
En el argumento anterior, podemos eliminar todo lo sombreado de
la tabla de verdad, ya que no nos interesa saber si la conclusión
es verdadera o falsa, cuando algunas premisas son falsas
p→q
q→r
∴ p→r
p q r p→q q→r (p→q)ʌ(q→r)) p→r (p→q)ʌ(q→r))→(p→r)
V V V V V V V V
V V F V F F F V
V F V F V F V V
V F F F V F F V
F V V V V V V V
F V F V F F V V
F F V V V V V V
F F F V V V V V
la conclusión es verdadera cuando
las premisas son verdaderas
Premisas Conclusión

10. Pasos para verificar la validez de un argumento
1. Identifique las premisas y la conclusión de la forma de
argumento.
2. Construya una tabla de verdad que incluya todas las premisas y
la conclusión.
3. Señale los renglones en el que todas las premisas son verdaderas
(renglones críticos).
4. Si hay un renglón crítico en el que la conclusión es falsa, la forma
del argumento es no válida. Si la conclusión en cada renglón
crítico es verdadera, entonces la forma del argumento es válida.
Observa que si en un renglón, una
premisa es falsa, no es necesario
continuar con las demás columnas
p→q
q→r
∴ p→r
p q r p→q q→r p→r
V V V V V V
V V F V F
V F V F
V F F F
F V V V V V
F V F V F
F F V V V V
F F F V V V
En nuestro ejemplo anterior:
En cada renglón critico, la conclusión es
verdadera, el argumento es valido

11. Formas de Argumento Válidas

12. Modus Ponens (Razonamiento directo)
“Si p implica q, y si p es verdadera,
entonces q debe ser verdadera.”
Ejemplo:
Si las rosas son rojas y las violetas son azules, entonces el azúcar
es dulce y tu también.
Las rosas son rojas y las violetas son azules.
• Por lo tanto, el azúcar es dulce y tu también.
p→q
p
∴ q
En símbolos: En palabras:
Observación: En la convención usada
en la tabla de formas de argumentos
validas no significa que p, q y r sean
proposiciones simples, también
pueden ser compuestas como en este
ejemplo
El ejemplo en símbolos:
(p^q)→(r^s)
p^q
∴ r^s

13. Modus Tollens (Razonamiento indirecto)
“Si p implica q, y q es falsa, entonces p es
falsa también.”
Ejemplo:
Si José nació en California, seria estadounidense
José no es estadounidense.
• Por lo tanto, no nació en California
p→q
~q
∴ ~p
En símbolos: En palabras:
IMPORTANTE: Un error común es pensar que si p implica q, y q es verdadera,
se sigue que p es verdadera ¿Cómo seria en símbolos?
“Si fuera estadounidense hablaría ingles, y yo hablo ingles, así que soy
estadounidense” (argumento no valido)
Esto error se llama la falacia de afirmar el consecuente o error converso.
Otro error común es pensar que si p implica q, y p es falsa, se sigue que q es
falsa. En nuestro ejemplo, ¿si José no nació en California, es garantía que no
es estadounidense?
Esto error se llama falacia de negar el antecedente o error contrario.

14. Simplificación (Especialización)
“Si p y q son verdaderas, entonces en particular
p es verdadera.”
*igual para q en el otro caso”
Ejemplo:
El cielo es azul y la luna es redonda.
• Por lo tanto, el cielo es azul.
p^q
∴ p
En símbolos: En palabras:
Adición (Generalización)
“Si p es verdadera, entonces sabemos que p
o q es verdadera.”
Ejemplo:
El cielo es azul.
• Por lo tanto, el cielo es azul
ó los perros vuelan
p
∴ pvq
En símbolos: En palabras:
No importa lo que utilizamos como q,
tampoco importa si q es verdadera o falsa.
La disyunción es verdadera si una de los dos
proposiciones es verdadera

15. Eliminación (Silogismo disyuntivo)
“Si p o q, es verdadera, y p es falsa,
entonces q es verdadera .”
*Similar si q es falsa, p es verdadera
Ejemplo:
José o Juan lo hicieron.
José no lo hizo.
• Por lo tanto, Juan lo hizo.
pvq
~p
∴ q
En símbolos: En palabras:
IMPORTANTE: Importante, no confundir la simplificación y la
adición, no son formas de argumento validas las siguientes:
p
∴ p^q
No se puede adicionar cualquier
proposición en forma de conjunción
pvq
∴ p
No se puede simplificar una
disyunción, sabe que p o q es
verdadera, pero no si ambas o cual