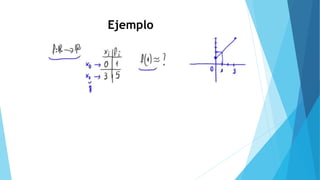
Este documento describe el método de interpolación polinómica de Lagrange. Explica que Lagrange publicó este método en 1795 para determinar un polinomio que interpola un conjunto de puntos dados. También discute que a medida que aumenta el grado del polinomio, aumentan las oscilaciones entre puntos consecutivos, limitando la validez del método.

1. Interpolación
Polinómica de Lagrange

2. INTRODUCCION
Los métodos para determinar una función polinomial que
nos permita determinar el valor en un punto dado, son:
1. Interpolación lineal simple
2. Método de Lagrange
3. Método de Newton.
Es importante aclarar que la interpolación se lleva a cabo a partir de
datos exactos, obtenidos de una función o de un comportamiento
periódico o de cifras exactas o valores bien conocidos.
Cuando se cuenta con datos obtenidos de mediciones se requiere
hacer un “ajuste de curvas” para obtener un valor.

3. HISTORIA
 El polinomio de Lagrange, llamado así en honor a Joseph-Louis de
Lagrange, es una forma de presentar el polinomio que interpola un
conjunto de puntos dado.
 Lagrange publicó este resultado en 1795, pero lo descubrió Edward
Waring en 1779 y fue redescubierto más tarde por Leonhard
Euler en 1783.
 Dado que existe un único polinomio interpolador para un
determinado conjunto de puntos, resulta algo engañoso llamar a
este polinomio el polinomio interpolador de Lagrange.
 Un nombre más apropiado es interpolación polinómica en la forma
de Lagrange.

4. DEFINICION
El polinomio de interpolación de Lagrange, simplemente
es una reformulación del polinomio de Newton que evita
los cálculos de las diferencias divididas.

5. DESVENTAJAS
• La tecnología actual permite manejar polinomios de grados
superiores sin grandes problemas, a costa de un elevado consumo
de tiempo de computación. Pero, a medida que crece el grado,
mayores son las oscilaciones entre puntos consecutivos o nodos.
• Se podría decir que a partir del grado 6 las oscilaciones son tal que
el método deja de ser válido, aunque no para todos los casos.
• Otra gran desventaja, respecto a otros métodos de interpolación, es
la necesidad de recalcular todo el polinomio si se varía el número
de nodos.

6. Ejemplo