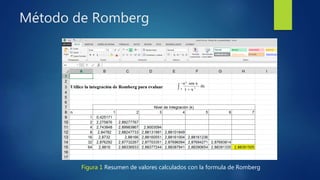
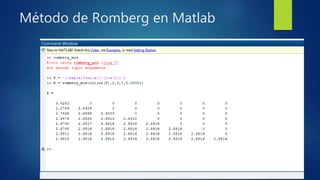
El método de Romberg es un método numérico para calcular integrales definidas que mejora la precisión de la regla del trapecio al aumentar el número de iteraciones. La fórmula de Romberg combina los resultados de la regla del trapecio con diferentes números de segmentos para generar estimaciones más precisas de la integral. El método se ilustra calculando la integral de 0 a 3 de e^x sen(x)/(1+x^2) dx, obteniendo un valor de 2.88391505 después de 7 iteraciones.

1. Método de Romberg
CLASE 14
23-JULIO-2014

2. Método de Romberg
 Al utilizar la regla del trapecio de segmentos múltiples y la regla de
Simpson de segmentos múltiples, se pudo observar que a medida que
aumentaba el numero de segmentos, 𝑛, el error disminuía; pero para
valores muy grandes de 𝑛, el error por redondeo empezaba a crecer y el
esfuerzo computacional se volvía grande.

3. Método de Romberg
 El método de integración de Romberg esta diseñado para evitar estos
inconvenientes y esta basado en la regla del trapecio, pero solo se puede
usar en casos en los que se conoce la función 𝑓(𝑥).
 La formula de Romberg es la siguiente:
 𝐼𝑗,𝑘 =
4 𝑘−1 𝐼 𝑗+1,𝑘−1−𝐼 𝑗,𝑘−1
4 𝑘−1−1
… … … … … … … … … … … … … … … . (1)

4. Método de Romberg
 Donde:
 𝐼𝑗+1,𝑘−1 𝑒 𝐼𝑗,𝑘−1; son las integrales mas y menos exactas,
respectivamente e 𝐼𝑗,𝑘 es la integral mejorada.
 𝑘 indica el nivel de integración
 𝑗 evaluaciones de la regla del trapecio.

5. Método de Romberg
 Donde:
 𝑒 𝑝 =
𝐼 𝑗,𝑘−𝐼 𝑗,𝑘−1
𝐼 𝑗,𝑘
100 … … … … … … … … … … … … … … . . (2)

6. Método de Romberg
 Precauciones que se deben tener en cuenta al usar este método:
 El paso no debe ser muy pequeño para que no se incremente el error por redondeo.
 Este método se utiliza en el caso en que se requiera mayor precisión en el calculo de la
integral.
 El nivel 𝑘 = 1 corresponde a la estimación de la regla del trapecio original.
 El nivel 𝑘 = 2 corresponde a una aproximación con un orden de error 𝑂 ℎ4
.
 El nivel 𝑘 = 3 corresponde a una aproximación con un orden de error 𝑂 ℎ6
y así
sucesivamente.

7. Método de Romberg
 Ejemplo
 Utilice la integración de Romberg para evaluar

0
3 𝑒 𝑥 𝑠𝑒𝑛 𝑥
1+𝑥2 𝑑𝑥

8. Método de Romberg
 Solución
 Se trabajara inicialmente con la regla del Trapecio, para
generar los datos del nivel 𝑘 = 1, calculando la integral con
distintos números de segmentos, los cuales deben irse
duplicando hasta que la variación de las integrales sea
mínima.

9. Método de Romberg
 Solución
 Se comienzan los cálculos con los valores mostrados en la
Tabla 1, los cuales se obtuvieron para los diferentes tamaños
de paso indicados.

10. Tabla 1 Valores iniciales para el calculo de la integral con la formula
de Romberg
𝒌 = 𝟏
𝑛 ℎ =
𝑏 − 𝑎
𝑛
𝐼 ℎ 𝑛 =
𝑏 − 𝑎
2(𝑛)
𝑓 𝑥0 + 2
𝑖=1
𝑛−1
𝑓 𝑥𝑖 + 𝑓 𝑥 𝑛
𝐼𝑛𝑡𝑒𝑔𝑟𝑎𝑙
1 3
𝐼 ℎ1 =
3 − 0
2
𝑒3 𝑠𝑒𝑛(3)
1 + 32
+
𝑒0 𝑠𝑒𝑛(0)
1 + 02
𝐼1,1 = 0.42517
2 1.5 𝐼 ℎ2 =
3 − 0
2 2
𝑒3
𝑠𝑒𝑛(3)
1 + 32
+ 2
𝑒1,5
𝑠𝑒𝑛(1.5)
1 + 1.52
+
𝑒0
𝑠𝑒𝑛(0)
1 + 02
𝐼2,1 = 2.275876
4 0.75 𝐼 ℎ3 =
3 − 0
2 4
𝑒3 𝑠𝑒𝑛(3)
1 + 32
+ 2
𝑒2.25 𝑠𝑒𝑛(2.25)
1 + 2.252
+
𝑒1.5 𝑠𝑒𝑛(1.5)
1 + 1.52
+
𝑒0.75 𝑠𝑒𝑛(0.75)
1 + 0.752
+
𝑒0 𝑠𝑒𝑛(0)
1 + 02
𝐼3,1 = 2.743848
8 0.375
𝐼 ℎ4 =
3 − 0
2(8)
𝑒3
𝑠𝑒𝑛(3)
1 + 32 + 2 … . +
𝑒0
𝑠𝑒𝑛(0)
1 + 02
𝐼4,1 = 2.84782
16 0.1875
𝐼 ℎ4 =
3 − 0
2(16)
𝑒3
𝑠𝑒𝑛(3)
1 + 32
+ 2 … . +
𝑒0
𝑠𝑒𝑛(0)
1 + 02
𝐼5,1 = 2.87320
32 0.09375
𝐼 ℎ4 =
3 − 0
2(32)
𝑒3 𝑠𝑒𝑛(3)
1 + 32
+ 2 … . +
𝑒0 𝑠𝑒𝑛(0)
1 + 02
𝐼6,1 = 2.876292

11. Método de Romberg
 Solución
 La cual se completa para los niveles 𝑘 = 2, 3, 4, 5, 6 𝑦 7
aplicando la formula de Romberg, de este modo se tiene:
 Para 𝑘 = 2 y haciendo variar 𝑗 desde 1 hasta 5

12. Método de Romberg
 𝐼𝑗,𝑘 =
4 𝑘−1 𝐼 𝑗+1,𝑘−1−𝐼 𝑗,𝑘−1
4 𝑘−1−1
, 𝑐𝑜𝑛 𝑘 = 2
 𝐼1,2 =
42−1 𝐼1+1,2−1−𝐼1,2−1
42−1−1
=
41 𝐼2,1−𝐼1,1
41−1
=
4 2.2758757−0.4251706
3
= 2.89277
 𝐼2,2 =
42−1 𝐼2+1,2−1−𝐼2,2−1
42−1−1
=
41 𝐼3,1−𝐼2,1
41−1
=
4 2.743884−2.2758757
3
= 2.89983
 𝐼3,2 =
42−1 𝐼3+1,2−1−𝐼3,2−1
42−1−1
=
41 𝐼4,1−𝐼3,1
41−1
=
4 2.8478324−2.74388479
3
= 2.882494

13. Método de Romberg
 𝐼𝑗,𝑘 =
4 𝑘−1 𝐼 𝑗+1,𝑘−1−𝐼 𝑗,𝑘−1
4 𝑘−1−1
, 𝑐𝑜𝑛 𝑘 = 2
 𝐼4,2 =
42−1 𝐼4+1,2−1−𝐼4,2−1
42−1−1
=
41 𝐼5,1−𝐼4,1
41−1
=
4 2.8732075−2.8478324
3
= 2.8816659
 𝐼5,2 =
42−1 𝐼5+1,2−1−𝐼5,2−1
42−1−1
=
41 𝐼6,1−𝐼5,1
41−1
=
4 2.8762921−2.8732075
3
= 2.8773203

14. Método de Romberg
 Solución
 Se procede de igual manera para 𝑘 = 3, y haciendo variar 𝑗
desde 1 hasta 4, y luego con 𝑘 = 4, 5, 6 𝑦 7, tal como se
muestra en la figura 1.

15. Método de Romberg
Figura 1 Resumen de valores calculados con la formula de Romberg

16. Método de Romberg
 Solución
 Para 𝑛 = 64 y después de siete iteraciones el valor de la
integral es 𝐼 = 2.88391505

17. Método de Romberg en Matlab
 Código de Matlab dado a continuación también se puede
utilizar para ejecutar el método de integración de Romberg.

18. Método de Romberg en Matlab

19. Método de Romberg en Matlab
 Ejecutamos la función anterior, para comprobar el ejercicio en
Excel.

20. Método de Romberg en Matlab
 Ejecutamos la función anterior, para comprobar el ejercicio en
Excel.

21. Método de Romberg en Matlab