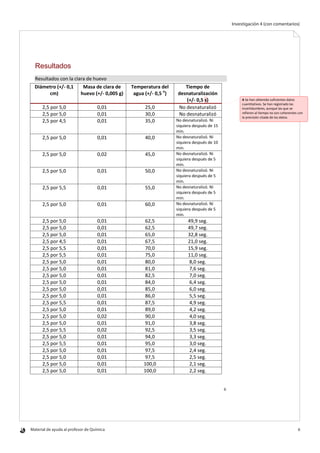
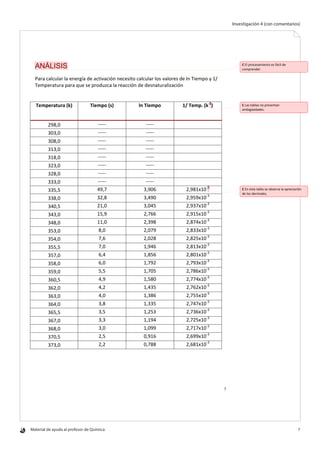
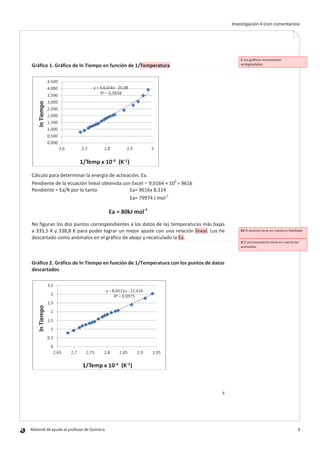
Este documento describe una investigación sobre cómo depende la velocidad de desnaturalización de las proteínas de la clara de huevo de la temperatura. El objetivo era determinar experimentalmente la energía de activación del proceso de desnaturalización midiendo el tiempo que tardaba la clara de huevo en desnaturalizarse a diferentes temperaturas y usando la ecuación de Arrhenius. Se midió el tiempo de desnaturalización de la clara de huevo entre 62,5°C y 100°C, y se calculó ln(tiempo) y 1/temperatura para graficar