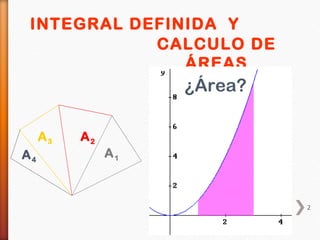
El documento explica los conceptos básicos de las integrales definidas y el cálculo de áreas. Define la integral definida como el límite de la suma de las áreas de los rectángulos de aproximación bajo la curva. Explica el Teorema Fundamental del Cálculo y algunas propiedades importantes de las integrales definidas como la linealidad y la propiedad aditiva respecto al intervalo de integración. Finalmente, presenta ejemplos de cómo calcular el área entre curvas y bajo curvas.

1. » MS. LUIS J. CASTILLO V.
1

2. INTEGRAL DEFINIDA Y
CALCULO DE
ÁREAS
¿Área?
A3 A2
A4 A1
2

3. 3

4. f (x) = e + 1 x
∆x
Definición : El área de la región S que se
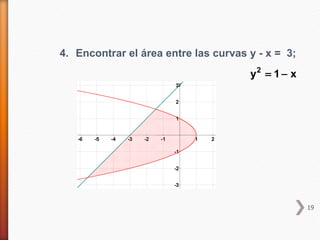
encuentra debajo de la gráfica de la función
continua f es el límite de la suma de las áreas
de los rectángulos de aproximación:
[( ) ( ) ( ) ]
n
A = lim ∑ Ai = lim f x ∆ x + f x2 ∆ x + ... + f xn ∆ x
* * * 4
1
n→ ∞ n→ ∞
i=1

5. b n
∫ f ( x )dx = lim ∑ f ( x *i )∆x i
n →∞
a i =1
b No tiene
∫
Limite significado,
superior
f ( x )dx indica respecto a
que variable se
a integra.
Integrando
Limite Inferior
El procedimiento para calcular 5
integrales se llama por si mismo
integración.

6. 2° Teorema Fundamental del Cálculo
Si f es una función continua en [a, b]
y F una antiderivada de f en [a, b], entonces:
b b
∫ a
f ( x) dx = F ( x) = F (b) − F (a)
a
Esta regla convierte al cálculo de integrales
definidas en un problema de búsqueda de
antiderivadas y evaluación. 6

7. PROPIEDADES DE LA
INTEGRAL DEFINIDA
1. Si f y g son funciones integrables
en [a, b] y α y β son constantes, se
tiene:
b b b
∫
a
(α f (x ) + β g ( x )) dx = α ∫
a
f (x ) dx + β ∫
a
g (x ) dx
Propiedad de linealidad
7

8. 1. Si existen las integrales de la
izquierda, también existe la integral de
la derecha: c ∈ a, b
c b b
∫a
f (x ) dx + ∫
c
f (x ) dx = ∫
a
f (x ) dx
Propiedad aditiva respecto
al intervalo de integración
8

9. La propiedad anterior es aplicada cuando la
función está definida por partes y cuando es
seccionalmente continua.
Ejemplo:
Si x 2 0 ≤ x ≤1
f ( x) = 
x - 1 1< x ≤ 3
y se quiere hallar: 3
∫ f ( x ) dx
0
3 1 3
∫ f (x)dx = ∫ x dx + ∫ (x − 1) dx
2
0 0 1
9

10. 3. b
∫ a
h dx = h ( b − a )
Y representa el área de un rectángulo de altura
h y longitud de base (b – a).
10

11. DEFINICIONES:
Sea f una función integrable en
[a, b], entonces:
a
1. ∫
a
f (x ) dx = 0
b a
2. ∫
a
f (x ) dx = − ∫
b
f (x ) dx
11

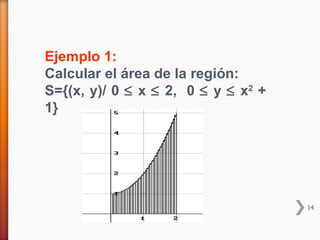
12. Definición:
Sea f una función contínua tal que:
• f(x) ≥0 en [a, b] y
• S={(x, y)/ a≤x≤b, 0≤y≤f(x)}
Se denota por A(S) y se llama área de
la región definida por S al número
dado por:
b
A(S) = ∫ f (x) dx
a
12

13. y
f(x)
y = f(x)
dx
dA = f(x)dx
b
dx ∆x
0 a b x A = ∫ f(x)dx
13
a

14. Ejemplo 1:
Calcular el área de la región:
S={(x, y)/ 0 ≤ x ≤ 2, 0 ≤ y ≤ x2 +
1}
14

15. y
d g(y)
dy
x = g(y)
dy
dA = g(y)dy
c
d
∫
0 x A = g(y)dy
15
c

16. Ejemplo 2:
Hallar el área de la región limitada
por y = 2x, y = (x-2)2 + 1, x = 3 y el
eje X, tal como lo muestra la figura.
16

17. f(x)
y - g(x)
y = f(x)
dx
0 a dx b x dA =[f(x) - g(x)]dx
b
y = g(x) A= ∫ [ f(x) - g(x)]dx
17
a

18. 3. Encontrar el área entre las curvas y = x - x3 ;
y = x 1− x2
y
1
x
-1 1
-1
18

19. 4. Encontrar el área entre las curvas y - x = 3;
y2 = 1 − x
19