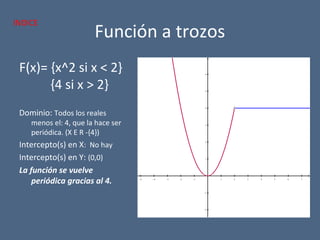
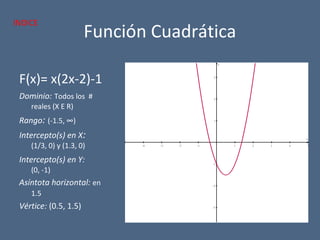
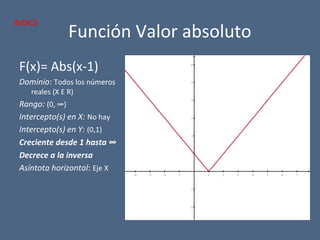
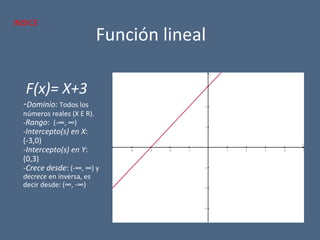
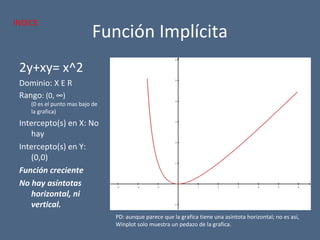
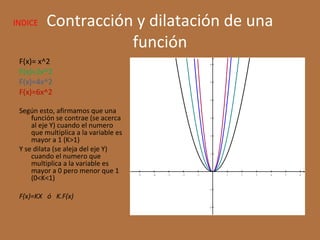
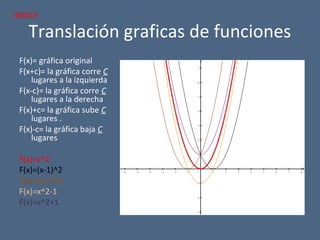
El documento detalla diferentes tipos de funciones matemáticas, incluyendo funciones algebraicas y trascendentes, y proporciona ejemplos de cada una con sus respectivos dominios, rangos e intersecciones. También se abordan conceptos como asíntotas, funciones par e impar, y la contracción y dilatación de gráficos. Además, se discute la translación de gráficas y se presentan ejemplos ilustrativos de funciones y sus características gráficas.

1. Funciones
• Algebraicas:
- Racionales
- Irracionales
- Radicales
- A trozos
- Polinómicas (cuadráticas)
- Valor Absoluto
- Lineales
• Trascendentes:
-Exponenciales
-Logarítmicas
• Tipo de funciones:
- Par
- impar
- Implícita
• Gráficas:
- Dilatación y contracción
- Traslación
- Dominio, Rango e Intercepto(s)
Nombre: Joshua Villamizar León
Curso: 11-02
Profesor: Manuel Padilla
Colegio: Policarpa Salavarrieta

2. Función racional
F(x)=(2x^2+1)/(x^4-1)
Dominio: Todos los reales
menos: -1 y 1
(X E R -{-1, 1})
Intercepto en X: no hay
Intercepto en Y: (0,-1)
La grafica se divide en
3 pedazos.
Asíntota Vertical: -1 y 1
Asíntota horizontal: el eje X
−4 −3 −2 −1 1 2 3 4 5
−3
−2
−1
1
2
3
x
y
INDICE

3. Función irracional
F(x)= x-sqr(x^2-1)
Dominio: Todos los reales
menos el conjunto de
números desde -1
hasta 1 ( X E R -(-1,1))
Asíntota Vertical: -1 y 1
Asíntota Horizontal: -1 y 1
La grafica se parte en
2 pedazos.
No hay intercepto ni en
X, ni en Y.
−3 −2 −1 1 2 3 4 5 6
−4
−3
−2
−1
1
2
x
y
INDICE

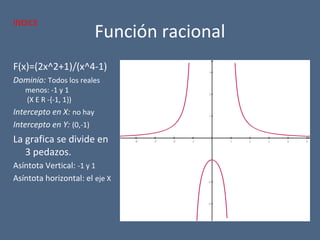
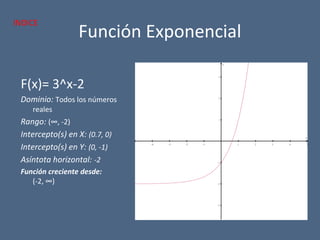
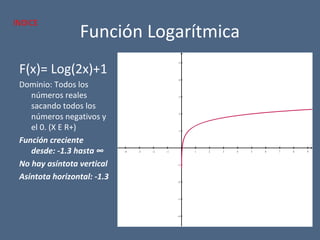
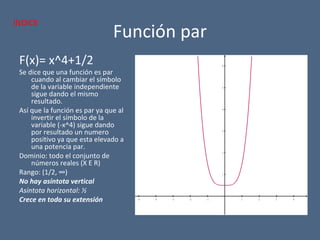
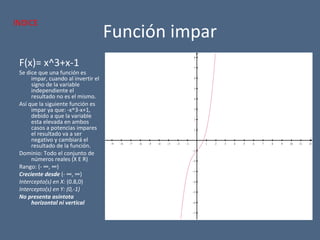
4. Función radical
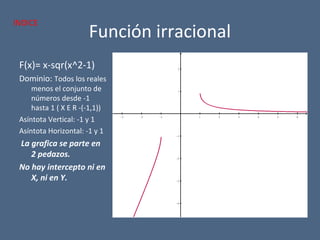
F(x) = sqr[(x+4)/(x^2-5x+6)]
Dominio: Todos los reales
menos el rango de
números desde el -4 hasta
-∞, también el rango de
números desde 2 hasta 3.
[X E R -((-4,-∞) U (2,3))]
Asíntota vertical: 2 y 3
Asíntota horizontal: El eje X
No presenta intercepto en el
eje X
Intercepto en Y: (0,0.8)
Crece desde: 0 hasta ∞
−4 −3 −2 −1 1 2 3 4 5 6 7 8 9 10 11
−2
−1
1
2
3
4
5
6
7
8
9
x
y
INDICE

5. Función a trozos
F(x)= {x^2 si x < 2}
{4 si x > 2}
Dominio: Todos los reales
menos el: 4, que la hace ser
periódica. (X E R -{4})
Intercepto(s) en X: No hay
Intercepto(s) en Y: (0,0)
La función se vuelve
periódica gracias al 4. −5 −4 −3 −2 −1 1 2 3 4 5 6 7
−2
−1
1
2
3
4
5
6
x
y
INDICE

6. Función Cuadrática
F(x)= x(2x-2)-1
Dominio: Todos los #
reales (X E R)
Rango: (-1.5, ∞)
Intercepto(s) en X:
(1/3, 0) y (1.3, 0)
Intercepto(s) en Y:
(0, -1)
Asíntota horizontal: en
1.5
Vértice: (0.5, 1.5)
−4 −3 −2 −1 1 2 3 4 5
−3
−2
−1
1
2
3
x
y
INDICE

7. Función Valor absoluto
F(x)= Abs(x-1)
Dominio: Todos los números
reales (X E R)
Rango: (0, ∞)
Intercepto(s) en X: No hay
Intercepto(s) en Y: (0,1)
Creciente desde 1 hasta ∞
Decrece a la inversa
Asíntota horizontal: Eje X
−4 −3 −2 −1 1 2 3 4 5 6 7
−2
−1
1
2
3
4
5
6
x
y
INDICE

8. Función lineal
F(x)= X+3
-Dominio: Todos los
números reales (X E R).
-Rango: (-∞, ∞)
-Intercepto(s) en X:
(-3,0)
-Intercepto(s) en Y:
(0,3)
-Crece desde: (-∞, ∞) y
decrece en inversa, es
decir desde: (∞, -∞)
−4 −3 −2 −1 1 2 3 4 5
−3
−2
−1
1
2
3
x
y
INDICE

9. Función Exponencial
F(x)= 3^x-2
Dominio: Todos los números
reales
Rango: (∞, -2)
Intercepto(s) en X: (0.7, 0)
Intercepto(s) en Y: (0, -1)
Asíntota horizontal: -2
Función creciente desde:
(-2, ∞)
−4 −3 −2 −1 1 2 3 4 5
−3
−2
−1
1
2
3
x
y
INDICE

10. Función Logarítmica
F(x)= Log(2x)+1
Dominio: Todos los
números reales
sacando todos los
números negativos y
el 0. (X E R+)
Función creciente
desde: -1.3 hasta ∞
No hay asíntota vertical
Asíntota horizontal: -1.3
−4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−4
−3
−2
−1
1
2
3
4
5
x
y
INDICE

11. Función par
F(x)= x^4+1/2
Se dice que una función es par
cuando al cambiar el símbolo
de la variable independiente
sigue dando el mismo
resultado.
Así que la función es par ya que al
invertir el símbolo de la
variable (-x^4) sigue dando
por resultado un numero
positivo ya que esta elevado a
una potencia par.
Dominio: todo el conjunto de
números reales (X E R)
Rango: (1/2, ∞)
No hay asíntota vertical
Asíntota horizontal: ½
Crece en toda su extensión −5 −4 −3 −2 −1 1 2 3 4
1
2
3
4
5
6
x
y
INDICE

12. Función impar
F(x)= x^3+x-1
Se dice que una función es
impar, cuando al invertir el
signo de la variable
independiente el
resultado no es el mismo.
Así que la siguiente función es
impar ya que: -x^3-x+1,
debido a que la variable
esta elevada en ambos
casos a potencias impares
el resultado va a ser
negativo y cambiará el
resultado de la función.
Dominio: Todo el conjunto de
números reales (X E R)
Rango: (- ∞, ∞)
Creciente desde (- ∞, ∞)
Intercepto(s) en X: (0.8,0)
Intercepto(s) en Y: (0,-1)
No presenta asíntota
horizontal ni vertical
−9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9 10 11 12
−7
−6
−5
−4
−3
−2
−1
1
2
3
4
5
6
7
8
x
y
INDICE

13. Función Implícita
2y+xy= x^2
Dominio: X E R
Rango: (0, ∞)
(0 es el punto mas bajo de
la grafica)
Intercepto(s) en X: No
hay
Intercepto(s) en Y:
(0,0)
Función creciente
No hay asíntotas
horizontal, ni
vertical.
−3 −2 −1 1 2 3 4 5 6
−1
1
2
3
4
5
6
x
y
PD: aunque parece que la grafica tiene una asíntota horizontal; no es así,
Winplot solo muestra un pedazo de la grafica.
INDICE

14. Contracción y dilatación de una
función
F(x)= x^2
F(x)=2x^2
F(x)=4x^2
F(x)=6x^2
Según esto, afirmamos que una
función se contrae (se acerca
al eje Y) cuando el numero
que multiplica a la variable es
mayor a 1 (K>1)
Y se dilata (se aleja del eje Y)
cuando el numero que
multiplica a la variable es
mayor a 0 pero menor que 1
(0<K<1)
F(x)=KX ó K.F(x)
−5 −4 −3 −2 −1 1 2 3 4 5 6
−2
−1
1
2
3
4
5
6
x
y
INDICE

15. Translación graficas de funciones
F(x)= gráfica original
F(x+c)= la gráfica corre C
lugares a la izquierda
F(x-c)= la gráfica corre C
lugares a la derecha
F(x)+c= la gráfica sube C
lugares .
F(x)-c= la gráfica baja C
lugares
F(x)=x^2
F(x)=(x-1)^2
F(x)=(x+1)^2
F(x)=x^2-1
F(x)=x^2+1
−6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8
−3
−2
−1
1
2
3
4
5
6
7
x
y
INDICE

16. Dominio, rango e intercepto(s)
Dominio: es el conjunto de números que puede llegar a
tomar la variable independiente, es decir: F(x)=x^2, en esta
función el dominio es el conjunto de todos los números reales
ya que no hay ningún numero que indetermine la función.
Rango: El rango de una función se halla despejando la variable
dependiente es decir: Y(f(x))= 2x-1, despejamos: Y+1=2x, así
que: X= (Y+1)/(2).
Intercepto(s): Es o son los puntos donde la gráfica corta el
eje X o el eje Y.
INDICE