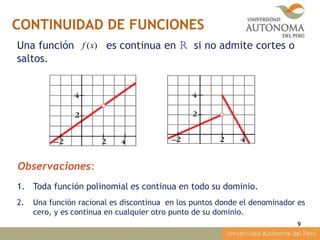
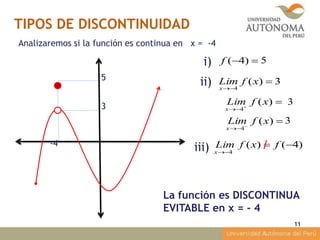
Este documento presenta los contenidos de la asignatura de Matemáticas 1 para el semestre 2014-II. Los contenidos incluyen la aplicación de límites y el concepto de continuidad de funciones. Se proveen ejemplos para ilustrar cómo calcular límites y analizar la continuidad de funciones en diferentes puntos. El documento concluye explicando cómo determinar si una función es continua a partir de analizar su gráfica.

1. SEMESTRE ACADÉMICO 2014-II
Agosto 2010
“Firmes en nuestro compromiso de alcanzar nuestra
visión de ser competitivos e innovadores para tener
acreditación internacional y contribuir al desarrollo
sostenido.”
MATEMÁTICA 1
 Aplicación de los
límites
 Continuidad
1

2. 2
 Aplicación de límites
 Continuidad
CONTENIDOS

3. 𝒍𝒊𝒎
𝒙→𝒂
𝒇 𝒙 = 𝑳
Si no existe tal número, se dice que el límite no existe.
El límite de 𝒇(𝒙) es 𝑳 ,cuando 𝒙 tiende a 𝒂
Límite de una función
Si,
𝒇(𝒙) se acerca cada vez más a 𝑳 cuando 𝒙 se acerca cada vez más a 𝒂
El límite (𝑳) es un número real
𝑦 = 𝑓(𝑥)
𝒂
𝑳
Geométricamente

4. El volumen de una piscina que se vacía viene expresado,
en función del tiempo 𝒕 minutos, por 𝑽 𝒕 =
𝟐− 𝒕−𝟑
𝟕−𝒕
𝒎 𝟑.
¿A qué valor se aproxima el volumen cuando el tiempo se
aproxima a 7 minutos?
Ejemplo de aplicación de límite

5. La Producción 𝑷 de cierto bien con respecto a la cantidad
de materia prima 𝒒 en kilogramos, es 𝑷 𝒒 =
𝒒 𝟐−𝟒
𝒒−𝟐
.
Calcule la producción cuando se acerca a 2 Kg. de materia
prima.
Ejemplo de aplicación de límite

6. Cierta función de Costo se define como 𝑪 𝒙 =
𝟒𝒙 𝟐−𝟏𝟎𝟎
𝒙−𝟓
,
en donde 𝒙 es el número de artículos producidos (en
cientos) y 𝑪 es el costo de producción (en miles de
soles).
Calcule e interprete 𝒍𝒊𝒎
𝒙→𝟓
𝑪(𝒙)
Ejemplo de aplicación de límite

7. Profesora: Risley Rengifo 7
Una constructora ha comprado una excavadora por 80 000
euros. El departamento financiero ha calculado que puede
revenderla al cabo de t años al precio de 𝒇 𝒕 =
𝟖𝟎
𝟏+𝟎.𝟒𝒕
miles de
euros.
Calcula el límite lim
𝑡→∞
𝒇(𝒕) y da una interpretación económica a
este resultado.

8. Profesora: Risley Rengifo 8
Se ha estimado que la población de un barrio periférico
de una gran ciudad evolucionará siguiendo este modelo:
𝑷 𝒕 =
𝟐𝟒𝟎+𝟐𝟎𝒕
𝟏𝟔+𝒕
miles de habitantes, donde t indica los
años transcurridos desde su creación en el año 2010.
Cuantos habitantes habrá a largo plazo

9. CONTINUIDAD DE FUNCIONES
9
Una función es continua en R si no admite cortes o
saltos.
)(xf
Observaciones:
1. Toda función polinomial es continua en todo su dominio.
2. Una función racional es discontinua en los puntos donde el denominador es
cero, y es continua en cualquier otro punto de su dominio.

10. CONTINUIDAD EN UN PUNTO
10
Una función es continua en a  R si y sólo
si., se cumple las siguiente tres condiciones:
)(xf
Exista , es decir)(af )( fDoma
)(xfLim
ax
)()( afxfLim
ax


Exista
i)
ii)
iii)
Si una función no es continua en un punto, se dice que es discontinua
en ese punto.

11. 11


)(
4
xfLim
x


)(
4
xfLim
x
 )4(f
)4()(
4


fxfLim
x
-4
3
5
i)
ii)
iii)
5
3
3
Analizaremos si la función es continua en x = -4
3)(
4


xfLim
x
La función es DISCONTINUA
EVITABLE en x = - 4
TIPOS DE DISCONTINUIDAD

12. TIPOS DE DISCONTINUIDAD


)(
1
xfLim
x


)(
1
xfLim
x
)1(fi)
ii)
5
5
7Analizaremos si la función es continua en x = 1
)(
1
xfLim
x
1
-5
7
12
La función es DISCONTINUA
INEVITABLE en x = 1
)1()(
1
fxfLim
x


iii)

13. Analice la continuidad de las siguientes funciones.
Determine el valor de las constantes, sabiendo que las funciones
son continuas en todo su dominio













1
3
12
1,
1
31
)()
2
x
x
x
x
xx
xfa









834
826
212
)()
xsix
xsi
xsix
xfb









2,33
2,24
2,12
)()
2
xmxn
xx
xnmx
xfb












1
213
1
113
)()
2
2
xsi
x
x
xsixax
xfa
13

14. Analiza la continuidad a partir de la gráfica de la
función dada.
-3 1 3
2
-1
4
-2
14

15. Ejemplo: aplicación de continuidad
Un comerciante vende un determinado producto, y por cada 𝒒
unidades cobra la siguiente cantidad:
𝑪 𝒒 =
𝟓𝒒, 𝟎 < 𝒒 ≤ 𝟏𝟎
𝒂𝒒 𝟐 + 𝟓𝟎𝟎, 𝒒 > 𝟏𝟎
Halla 𝒂 para que el precio varíe de forma continua al variar el número
de unidades que se compran.

16. En una práctica de Química se ha medido la temperatura de una
sustancia durante el transcurso de una reacción que dura 24 horas.
Las medidas obtenidas se ajustan a esta función, donde 𝒕 es el tiempo
en horas.
𝑻 𝒕 =
𝒕 𝟐 − 𝟏𝟏𝒕 − 𝟐, 𝟎 ≤ 𝒕 < 𝟏𝟐
𝟐𝒕 − 𝟏𝟒, 𝟏𝟐 ≤ 𝒕 < 𝟏𝟓
𝟔𝟒 −
𝟏𝟔
𝟓
𝒕, 𝟏𝟓 ≤ 𝒕 < 𝟐𝟒
Estudia si la temperatura es una función continua.
Ejemplo: aplicación de continuidad

17. A los 20 años de su fundación, una empresa realizó un cambio en
la forma de realizar su contabilidad. Sus beneficios, en millones
de euros, se calculan con esta función.
𝑩 𝒕 =
𝟑𝒕 + 𝟏𝟎
𝒕
, 𝟎 < 𝒕 ≤ 𝟐𝟎
𝒂𝒕 −
𝟏𝟗𝟑
𝟐
, 𝒕 > 𝟐𝟎
donde t es el número de años transcurridos.
¿Cuál debe ser el valor de 𝒂 para que el cambio en los beneficios
resulte continuo?
Ejemplo: aplicación de continuidad

18. TRABAJO EN EQUIPO