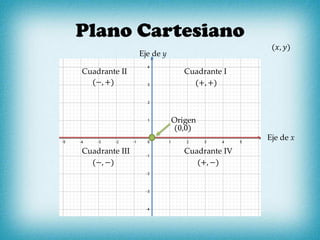
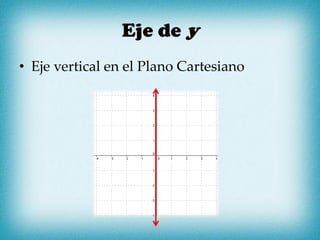
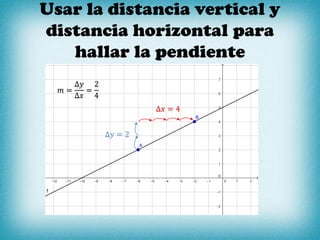
El documento presenta conceptos clave sobre pendientes y rectas en un plano cartesiano. Explica que la pendiente (también conocida como razón de cambio) es la variación en la coordenada y dividida por la variación en la coordenada x entre dos puntos en una recta. Proporciona fórmulas para calcular la pendiente usando coordenadas de puntos o distancias verticales y horizontales. También cubre casos especiales como pendientes de 0 e infinito y formas de ecuaciones lineales.

1. Razón de cambio
Pendiente
Prof. Rosa E. Padilla
Álgebra 1

2. Plano Cartesiano
Eje de y
Eje de x
Origen
Cuadrante ICuadrante II
Cuadrante III Cuadrante IV
(+, +)(−, +)
(−, −) (+, −)
(0,0)
(𝑥, 𝑦)

3. Eje de x
• Eje horizontal en el Plano Cartesiano

4. Eje de y
• Eje vertical en el Plano Cartesiano

5. Plano Cartesiano
(4,2)(−2,2)
(−3, −3)
(3, −1)
AB
C
D

6. Razón
• Comparación entre dos cantidades a
través de la división.
𝑎
𝑏
𝑏 ≠ 0

7. Razón de cambio
• También conocido como pendiente.
•
𝑐𝑎𝑚𝑏𝑖𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑐𝑎𝑚𝑏𝑖𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
•
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
•
∆𝑦
∆𝑥

8. Usar la distancia vertical y
distancia horizontal para
hallar la pendiente
Δ𝑦 = 2
Δ𝑥 = 4
𝑚 =
Δ𝑦
Δ𝑥
=
2
4

9. Usar la distancia vertical y
distancia horizontal para
hallar la pendiente
Δ𝑦 = −3
Δ𝑥 = 2
𝑚 =
Δ𝑦
Δ𝑥
= −
3
2

10. Usar coordenadas para hallar
la pendiente o razón de cambio
• Halla la pendiente de la recta que pasa por
C(-2,6) y D(4,3)
𝑚 =
∆𝑦
∆𝑥
=
𝑦2 − 𝑦1
𝑥2 − 𝑥1
=
3 − 6
4 − (−2)
=
−3
6
= −
1
2

11. Halla la pendiente de la recta
que pasa por los dos puntos
• V(8, -1), Q(0, -7)
• S(-4, 3), R(-10, 9)
(𝑥1, 𝑦1) (𝑥2, 𝑦2)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1
𝑚 =
−7 − (−1)
0 − 8
=
−6
−8
=
6
−6
(𝑥1, 𝑦1) (𝑥2, 𝑦2)
𝑚 =
9 − 3
−10 − (−4)
=
3
4
= −1

12. Halla la pendiente de la recta
que pasa por los dos puntos
1. A(2,6), B(8,1)
2. E(1,-2), F(4,-8)
3. N(-5,2), Q(1,-4)
4. G(3,4), H(6,10)
5. P(-3,0), Q(4,-5)
6. A(2,4), B(-1,-2)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1

13. Pendiente de casos especiales
(−2, −3) (4, −3)
𝑚 =
−3 − (−3)
4 − (−2)
𝑚 =
0
6
𝑚 = 0

14. Pendiente de casos especiales
(2,2)
(2, −2)
𝑚 =
−2 − 2
2 − 2
𝑚 =
−4
0
𝑚 = ∞

15. Forma “general” de una
ecuación lineal
• La forma general de una ecuación lineal
es:
Ax + By = C
• Donde A, B y C son números reales
mientras que A y B no son iguales a cero.

16. Forma “pendiente - intercepto”
de una ecuación lineal
• La forma pendiente – intercepto de una
ecuación lineal de una ecuación lineal es:
𝑦 = 𝑚𝑥 + 𝑏
• Donde m corresponde a la pendiente o
razón de cambio, mientras que b
corresponde al intercepto en el eje de y.

17. Intercepto
• El intercepto y de la recta es el punto
donde la línea cruza el eje de y.
• La constante de la ecuación es el
intercepto y.
• Ocurre cuando x=0.
𝑦 = −
1
2
𝑥 + 3

18. Identifica la pendiente y el
intercepto en cada ecuación
1. 𝑦 = 7𝑥 + 3
2. 𝑦 = 2𝑥 + 1
3. 𝑦 = 3
4. 𝑦 = −𝑥 − 4
5. 𝑦 = −𝑥
6. 𝑦 = −3𝑥 + 3
7. 𝑦 =
1
2
𝑥 − 8
8. 𝑦 = −3𝑥 − 8
9. 𝑦 = −
3
2
𝑥 + 6
10. 𝑦 =
4
5
𝑥 − 2

19. Halla la pendiente
usando una gráfica
• Pendiente =
𝑒𝑙𝑒𝑣𝑎𝑐𝑖ó𝑛
𝑟𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑜
• =
3−1
4−(−1)
• =
2
5
• La pendiente de la
recta es
2
5
.
(-1, 1)
(4, 3)
Subir 2
unidades
Derecha 5
unidades

20. Halla la pendiente
usando una gráfica
• Pendiente =
𝑒𝑙𝑒𝑣𝑎𝑐𝑖ó𝑛
𝑟𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑜
• =
2−5
4−(−1)
• =
−3
5
= −
3
2
• La pendiente de la
recta es −
3
2
.
(-1, 5)
(4, 2)
Bajar 3
unidades
Derecha 5
unidades

21. Hallar la pendiente
dados dos puntos
• Puedes usar dos puntos en cualquier
lugar de una recta para hallar su
pendiente.
• Usa subíndices para distinguir entre
los puntos.
• En el diagrama, 𝑥1, 𝑦1 son las
coordenadas del punto P y (𝑥2, 𝑦2) son
las coordenadas de Q.
• Para hallar la pendiente de la recta 𝑃𝑄
usamos la siguiente fórmula:
• Pendiente =
𝑒𝑙𝑒𝑣𝑎𝑐𝑖ó𝑛
𝑟𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑜
=
𝑦2−𝑦1
𝑥2−𝑥1
, donde
𝑥2 − 𝑥1 ≠ 0.
𝑦2 − 𝑦1
𝑥2 − 𝑥1
𝑃(𝑥1, 𝑦1)
𝑄(𝑥2, 𝑦2)

22. Pendientes de rectas
O x
y
O
x
O x
y
O x
Una recta con
pendiente
positiva
se inclina hacia
arriba de
izquierda
a derecha.
Una recta con
pendiente
igual a cero
es horizontal.
Una recta con
pendiente
negativa
se inclina hacia
abajo de
izquierda
a derecha.
y
y
Una recta con
pendiente
indefinida
es vertical.
𝑚 > 0 𝑚 < 0
𝑚 = 0
𝑚 = ∞

23. Halla la pendiente de cada
recta
1. 2.
(-2, 1)
(3, 4) (-3, 2)
(3, 1)

24. Halla la pendiente de cada
recta
3. 4.

25. Halla la pendiente de la recta que
pasa por cada par de puntos
1. (3, 2), (5, 6)
2. (5, 6), (3, 2)
3. (
1
2
, 8), (1, -2)
4. (-4, 4), (2, -5)
5. (-2, 1), (1, -2)
6. (4, 1
2
3
), (-2,
2
3
)
7. (5, 0), (0, 2)
8. (0, 0), (3, 5)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1