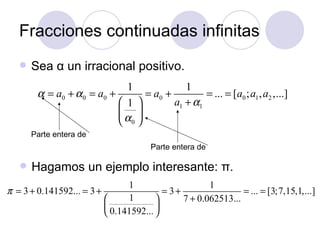
El documento explica cómo Pitágoras descubrió la relación entre las longitudes de cuerdas vibrantes y los intervalos musicales, lo que llevó al desarrollo de la escala musical occidental de 12 notas. Explica que aproximar de manera racional la razón log(3)/log(2) entre los intervalos de una quinta da como resultado 12 notas, y que este número representa el mejor compromiso entre recorrer el círculo de quintas y cerrar la escala en la octava.

1. Las Matemáticas y la Música. ¿ Porqué la escala musical occidental tiene 12 notas? 2o Residencial AFAMaC Arturo Portnoy Departamento de Matemáticas, UPRM

2. Pitágoras y la Música Un amor místico por las matemáticas y la música. Descubre que existe una relación entre monocordios de longitudes cuyas razones son “muy” racionales y la armonía de los sonidos que emiten. TODO ES NUMERO. Intervalos Pitagóricos: Octava (2/1), Quinta (3/2), Cuarta (4/3).

3. Demostraciones físicas y musicales Saltando la cuerda. El tubo que canta. Intervalos armónicos: generador de tonos

4. C í rculo de quintas Tono base: f. Quinta: (3/2)f. Quinta de la quinta (3/2) ²f. etc… ¿ Hasta cuando? Hasta cerrar en octava:

5. Algo de matemáticas Podemos reescribir la ecuación anterior: Esta ecuación no tiene solución en los enteros. ¿ Porqu é ? Lo mejor que podemos hacer es aproximar: Esto es un problema de aproximar un irracional con un racional. Recordemos que m representa el numero de notas en la escala. Notemos que de estar charlando sobre musiquita, anécdotas históricas, etc., de pronto, ¡ estamos hasta el cuello en matemáticas!

6. Aproximaciones racionales de irracionales Pensemos en un ejemplo famoso: π=3.14159265... Usualmente usamos la aproximación decimal: 3.1416=31416/10000. Hay aproximaciones mucho “mejores”, mas eficientes, que con un denominador menor, hacen mejor trabajo: 22/7=3.142857…, | π-22/7|<1/100<1/(7²) 355/113=3.14159292…, | π-355/113|<1/(100³)<1/(113²).

7. El Teorema de Dirichlet y el principio del palomar Si tenemos n+1 palomas y n palomares, al menos hay dos palomas durmiendo juntas. Sea a>0 el irracional que deseamos aproximar y sean a ·m- [a ·m], m=1,2,3,…,n+1 las n palomas. Dividamos el intervalo [0,1] en n partes iguales (estos son los n palomares). Entonces hay dos palomas en un palomar: Aproximación racional Denominador al cuadrado

8. Teorema de Dirichlet, fortalezas y debilidades Fortalezas: Argumento muy lindo, elegante, demuestra la existencia de una infinidad de estas “buenas” aproximaciones racionales para cualquier irracional. Debilidades: No nos dice como construir estas “buenas” aproximaciones… Nada mas nos antoja…

9. Como construir estas aproximaciones: fracciones continuadas Ejemplo: 19/12. Fracción continuada finita Notación para fracción continuada

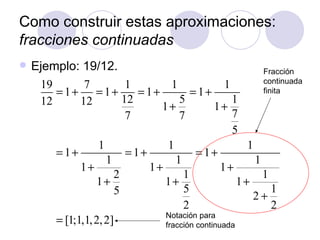
10. Nuevo concepto: convergente Sabemos ya que 19/12=[1;1,1,2,2]. Consideremos ahora los convergentes asociados a esta fracción continuada: Observemos ahora que: Por lo tanto:

11. Observaciones Los convergentes se van acercando al valor de la fracción continuada asociada. Lo hacen “acorralando” al valor de la fracción continuada: los convergentes pares por abajo, y los impares por arriba. Esto no lo hemos demostrado, solo sugerido, pero se demuestra en el m ó dulo que se entregar á .

12. Otras observaciones A cada racional le corresponde una sola fracción continuada finita, y cada fraccion continuada finita representa a un solo racional. Quizás podríamos hacer algo similar con los irracionales.

13. Fracciones continuadas infinitas Sea α un irracional positivo. Parte entera de Parte entera de Hagamos un ejemplo interesante: π.

14. Fracción continuada de π

15. Observaciones Los convergentes de las fracciones continuadas infinitas asociadas a un irracional son las “buenas” aproximaciones racionales que el teorema de Dirichlet nos asegura existen. De hecho, es posible demostrar que si una aproximación es “buena”, entonces es un convergente de la fracción continuada. Para mas detalles, ver el m ó dulo.

16. Volvamos al problema original Recordemos que el problema que nos arrastro en esta dirección es: Representa el numero de notas en la escala. Ya sabemos que las buenas aproximaciones son los convergentes, así que…

17. Fracción continuada de log(3)/log(2)

18. Observaciones Tienen que haber 12 notas en la escala. 5 son muy pocas, resulta en música aburrida (escala penta tónica, música oriental). 41 notas son demasiadas, ni un pulpo podría tocar el piano.

19. Otro ejemplo interesante: la razón áurea Razón áurea: La razón áurea es solución de: Observemos entonces que:

20. Ú ltimas observaciones Hemos visto que el deseo de recorrer el circulo de quintas y el de cerrar la escala en la octava son irreconciliables. El mejor compromiso es la escala de 12 notas. Sin embargo, no hemos discutido como vamos a corregir la escala de 12 notas para que cierre en la octava. ¿ Ponemos toda la corrección en la ultima nota? ¿ C ó mo hacemos?

21. Temperamentos de la escala musical Durante siglos, matemáticos y músicos han propuesto muchas soluciones a este problema. Una de ellas se llama la escala bien atemperada , y Bach le dedico a esta solución en el clavecín una serie de composiciones: El clavecín bien atemperado. La solución moderna es la escala equi-atemperada: La escala moderna permite transposiciones arbitrarias, sin que cambie el temperamento de la composición.