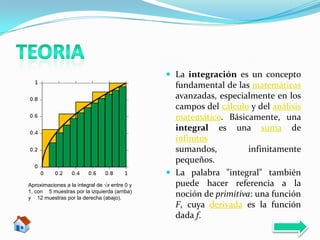
El documento proporciona instrucciones sobre cómo realizar integrales definidas e indefinidas. Explica que una integral definida calcula el área bajo una curva entre dos límites, mientras que una integral indefinida encuentra una función primitiva. A continuación, detalla los pasos para resolver cada tipo de integral y proporciona ejemplos ilustrativos.

1. •Hacer clic en el icono de inicio en la parte inferior derecha
Omar Alberto Torres Mijares. Grupo: 606

2. 1. Para iniciar a ver el contenido didáctico, da clic en cualquiera de los siguientes hipervínculos.
2. Para salir da clic en el siguiente icono
3. Para regresar a este menú da clic en este icono
TEORIA

3.  La integración es un concepto
fundamental de las matemáticas
avanzadas, especialmente en los
campos del cálculo y del análisis
matemático. Básicamente, una
integral es una suma de
infinitos
sumandos, infinitamente
pequeños.
 La palabra "integral" también
Aproximaciones a la integral de √x entre 0 y puede hacer referencia a la
1, con 5 muestras por la izquierda (arriba)
y 12 muestras por la derecha (abajo).
noción de primitiva: una función
F, cuya derivada es la función
dada f.

4.  El signo ∫, representa la
integración; a y b son el límite
inferior y el límite superior de la
integración y definen el dominio
de integración; f es el
integrando, que se tiene que
evaluar al variar x sobre el
intervalo [a,b]
 dx puede tener diferentes
interpretaciones dependiendo
de la teoría que se emplee. Las
integrales aparecen en muchas
situaciones practicas.

5.  Se puede encontrar dos tipos de integrales las definidas e
indefinidas.
 Las definidas hablan de una función continua y positiva en el
intervalo [a,b], la gráfica de la función y las rectas de ecuaciones x
=a, x=b, y = 0 definen una región que es la que se trata de calcular.
Ejemplo es la siguiente imagen. Y se utiliza la siguiente formula
Para calcular el área que encierra la función y= x+2, entre x=0, x=3 y el eje x

6.  El proceso de hallar la primitiva de una función se conoce como
integración indefinida* y es por tanto el inverso de la
derivación.
 Estas están relacionadas con las integrales definidas a través
del teorema fundamental del calculo, proporcionan un
método sencillo de calcular integrales definidas de numerosas
funciones.
*Cuando se trata de una integral indefinida siempre se pone una constante al finalizar, como se muestra en la
imagen
Para hacer una integral indefinida es preciso utilizar esta formula
Fuente: http://www.distrito22.com/mates/ffin.htm

7.  Para realizar una integral
definida:
 1. Integramos utilizando
esta formula
 2. A continuación se
sustituyen los valores, de
los limites: limite superior
menos limite inferior
(respectivamente) con la
sig. Formula
 3. Se restan y queda listo

8.  Para realizar una integral
indefinida:
 1. Integramos la función
usando:
 2. Hacemos las
operaciones algebraicas
necesarias

9.  Tenemos una integral definida como la siguiente:
 1. La integramos con la formula antes vista:
 Obtenemos lo siguiente:
 2. Sustituimos limite superior menos limite inferior
con la siguiente formula:
 Y tenemos lo siguiente:
 El resultado de la integral definida será 6

10.  Tenemos una integral indefinida como la siguiente:
 1. La integramos con la siguiente formula:
 Obtenemos lo siguiente:
 2. Siempre cuando sea una integral indefinida se pone
“C” por que no tiene limites como el caso de la
definida.
 El resultado es:

11. Instrucciones para llevar a cabo una integral definida:

12. Instrucciones para llevar a cabo una integral indefinida:

13.  Ahora estas listo para iniciar los siguientes ejercicios,
hay que seguir las siguientes instrucciones:
 1. Para iniciar es necesario púlsar la siguiente flecha:
 2. Para avanzar al siguiente ejercicio es necesario
responder correctamente. (de lo contrario no
avanzaras)
 3. Para regresar a menú es necesario pulsar el
siguiente icono:

14.  Encontrar el valor de las siguientes integrales:
 1.
A) 260 B) 268 C) 252 D) 264
 2.
A) 3.2 B) 3 C) 2.5 D) 2
 3.
A) 13 B) 15 C) 14 D) 7
 4.
A) 1 B) -1 C) 0 D) 2

15.  5. Encontrar el área entre la parábola “y= 4+2x” y el
eje “X” para “x” (2,5) Si 5 es lim. Sup. Y 2 es lim. Inf.
Àrea de la Integral
6
5
4
3
x
2
1
0
2 3 4 5
A) 35 B) 36 C)40 D) 33

16.  Encontrar el valor de las siguientes integrales:
 1.
A) x2 B) x3 + c C) x2 + c D) 2x+c
 2.
A) x6+c B) x7 +c C) x6 D) 6x+c
 3.
A) B) C) D)
 4.
A) B) C) D)

17.  http://tutorialmate.galeon.com/integrales.html
 http://www.distrito22.com/mates/ffin.htm
 http://es.wikipedia.org/wiki/Funci%C3%B3n_primitiv
a
 http://es.wikipedia.org/wiki/Teorema_fundamental_d
el_c%C3%A1lculo
 http://www.youtube.com/watch?v=fESUu8BXQaI&fea
ture=related
 http://www.youtube.com/watch?v=wTGiOyKrL8M