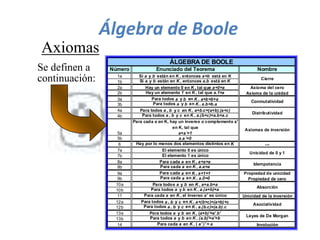
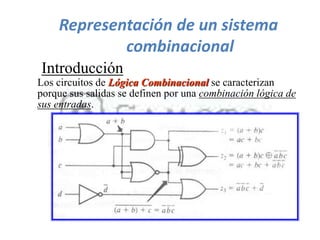
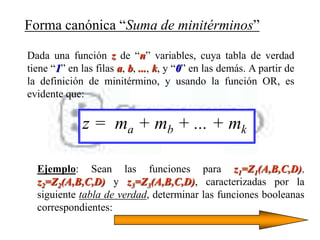
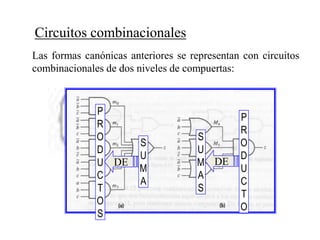
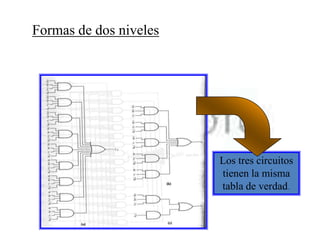
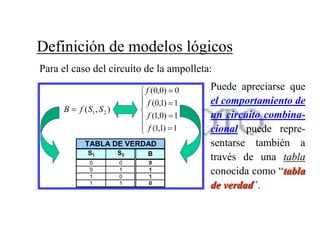
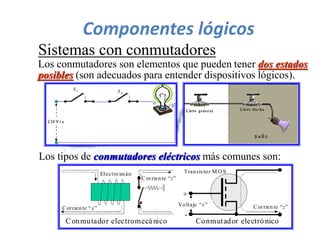
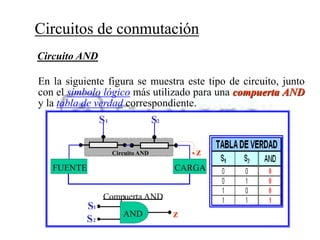
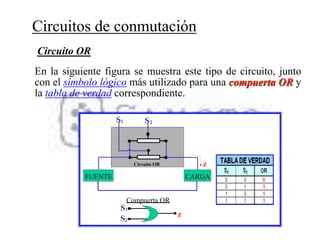
El documento describe los sistemas binarios y la lógica binaria. Un sistema binario utiliza dos valores posibles, generalmente representados por 1 y 0. La lógica binaria se usa en sistemas digitales debido a que los conmutadores solo tienen dos estados y los procesos de decisión son binarios. Las expresiones lógicas se pueden representar mediante tablas de verdad, circuitos lógicos y funciones booleanas.

1. LOGICA
BINARIA
Por: Salatiel Moreno Toro

2. Un sistema binario se caracteriza por tener dos valores
posibles que, en términos de voltaje, se corresponden a dos
valores de tensión, los que se representan numéricamente por
un “1” y por un “0”.
Generalmente, la “lógica positiva” hace corresponder un valor
de tensión alto al “1” y un valor de tensión bajo al “0” (y
viceversa para la “lógica negativa”):
Introducción a los sistemas
digitales
Sistemas binarios
PositivaLógica
alto)voltaje(1
bajo)voltaje(0





H
L
V
V

3. Números binarios
La correspondencia entre los
primeros 16 números decimales
y binarios se muestra en la
siguiente tabla:
N ú m er o de ci m a l N ú m e ro bin ar io
0 00 00
1 00 01
2 00 10
3 00 11
4 01 00
5 01 01
6 01 10
7 01 11
8 10 00
9 10 01
10 10 10
11 10 11
12 11 00
13 11 01
14 11 10
15 11 11
Mientras más dígitos tiene un
sistema, más compacta es su
notación. Así, los dígitos bina-
rios tienden a ser más largos (en
un factor log210=2,3222) que
su correspondiente nota-ción
decimal.

4. Las principales razones por las cuales utilizar sistemas de
representación binaria son:
Porqué usar la representación binaria
• Los sistemas de procesamiento de información se
construyen en base a conmutadores;
• Los procesos de toma de decisión, en un sistema
digital, son binarios; y
• Las señales binarias son más confiables que las que
tienen más niveles de cuantificación.

5. Conmutadores
Porqué usar la representación binaria
Supóngase un sistema de
iluminación basado en
dos interruptores o con-
mutadores (como el que
existe en la parte inferior y
superior de una escalera):
S1 S21
0
1
0
Ampolleta220V
S1 S21
0
1
0
A
  
   esConclusionoAcciones
A
A
premisasosCondicione
S
S
S
S
encendida)(ampolleta1
apagada)(ampolleta0
0)posiciónen2r(conmutado0
1)posiciónen2r(conmutado1
0)posiciónen1r(conmutado0
1)posiciónen1r(conmutado1
2
2
1
1







6. Toma de decisiones
Porqué usar la representación binaria
Gran parte de los procesos de decisión tienen carácter binario








 .Respuestas etc
INCORRECTO
CORRECTO
FALSO
VERDADERO
NO
SI
Un sistema puede ca-
racterizarse lingüísti-
camente como:
Si (S1=1 y S2=0) o (S1=0 y S2=1),
entonces B=1; caso contrario, B=0.
Confiabilidad
Las señales binarias son mucho más confiables para ser
transmitidas entre dos puntos distantes. Al usar sólo dos
niveles de voltaje para representar un dígito, el sistema es más
inmune a la presencia de ruidos.

7. Descripciones formales
Definición de modelos lógicos
Una descripción abstracta de un sistema digital, expresado
con enunciados lógicos formales, se denomina “DISEÑO
LÓGICO”.
Los símbolos más
comunes son: 







entonces
O
Y
Usando estos símbolos, el circuito de encendido de la
ampolleta puede representarse como:
           
           00011
10110
2121
2121


BSSSS
ó
BSSSS

8. Usando este tipo de representación, podría definirse la
operatoria de un sumador binario como:
o, en forma simbólica (para el caso de la “suma”), por:
0|111
1|001
1|010
0|000
|




 SumaAcarreoyx
X Y Acarreo Suma
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 1
Entradas Salidas
           
           00011
10110


Sumayxyx
ó
Sumayxyx
Definición de modelos lógicos

9. En caso de sistemas multivariables (varias entradas y salidas),
“x” será un vector de entradas y habrá una función asociada a
cada salida. Estas funciones también suelen denominarse
“funciones booleanas”, ya que responden al “álgebra de
Boole”.
Definición de modelos lógicos
Un comportamiento de un sistema combinacional puede
expresarse formalmente como z=f(x), donde “z” representa la
salida del sistema y “x” la entrada (para un sistema de una
entrada y una salida).

10. Para el caso del circuito de la ampolleta:
),( 21 SSfB 











1)1,1(
1)0,1(
1)1,0(
0)0,0(
f
f
f
f
S1 S2 B
0 0 0
0 1 1
1 0 1
1 1 0
TABLA DE VERDAD
Puede apreciarse que
el comportamiento de
un circuito combina-
cional puede repre-
sentarse también a
través de una tabla
conocida como “tabla
de verdad”.
Definición de modelos lógicos

11. Componentes lógicos
Sistemas con conmutadores
Los conmutadores son elementos que pueden tener dos estados
posibles (son adecuados para entender dispositivos lógicos).
Los tipos de conmutadores eléctricos más comunes son:
C orrien te “x”
C orrien te “z”
C orrien te “z”Voltaje “x”
+
-
Electro imán Transistor M O S
Conmutador electromecá nico Conmutador electró nico

12. Circuitos de conmutación
Circuito AND
En la siguiente figura se muestra este tipo de circuito, junto
con el símbolo lógico más utilizado para una compuerta AND
y la tabla de verdad correspondiente.
FUENTE CARGA
S1 S2
Circuito AND
ANAND
Compuerta AND
S1
S2
z
z

13. Circuitos de conmutación
Circuito OR
En la siguiente figura se muestra este tipo de circuito, junto
con el símbolo lógico más utilizado para una compuerta OR y
la tabla de verdad correspondiente.
FUENTE CARGA
S1 S2
Circuito OR
Compuerta OR
S1
S2
z
z

14. Circuitos de conmutación
Circuito NOT
En la siguiente figura se muestra este tipo de circuito, junto
con el símbolo lógico más utilizado para una compuerta NOT
y la tabla de verdad correspondiente.
FUENTE CARGA
S
Circuito NOT
Co mp uerta NOT
S z
z
1

15. Expresiones lógicas
Para expresar las funciones lógicas asociadas a cada uno de
los circuitos anteriores, se usan operadores lógicos.
zAND(x1, x2)=1 sí y sólo sí x1=1 Y x2=1zAND(x1, x2)=1 sí y sólo sí x1=1 Y x2=1
ZOR(x1, x2)=1 sí y sólo sí x1=1 O x2=1ZOR(x1, x2)=1 sí y sólo sí x1=1 O x2=1
2121 ),( xxxxzAND 
2121 ),( xxxxzOR 
ZNOT (x)=1 sí y sólo sí x=0
xxzNOT )(
Es importante
tener en cuenta
que los símbolos
“.” y “+” son
operadores
lógicos y NO
algebraicos.

16. Convenios de voltaje
Para la lógica TTL (“Transistor – Transistor Logic”) se
ha determinado un convenio de voltajes, para especificar
cuándo una entrada o salida se considera que tiene el valor
lógico correspondiente.
0,0
5,0
[V]
2,4
2,0
0,8
0,4
Invervalo VH
garantizado
para salidas = 1
Invervalo VH
aceptado para
entradas = 1
In vervalo V L acepta do
pa ra entradas = 0
Invervalo V L
garanti za do
para salidas = 0
LÓGICA TTL

17. Álgebra de Boole
Axiomas
Número Enunciado del Teorema Nombre
1a Si a y b están en K , entonces a+b está en K
1b Si a y b están en K , entonces a.b está en K
2a Hay un elemento 0 en K , tal que a+0=a Axioma del cero
2b Hay un elemento 1 en K , tal que a.1=a Axioma de la unidad
3a Para todos a y b en K , a+b=b+a
3b Para todos a y b en K , a.b=b.a
4a Para todos a , b y c en K, a+b.c=(a+b).(a+c)
4b Para todos a , b y c en K , a.(b+c)=a.b+a.c
Para cada a en K, hay un inverso o complemento a'
en K, tal que
5a a+a´=1
5b a.a´=0
6 Hay por lo menos dos elementos distintos en K ---
7a El elemento 0 es único
7b El elemento 1 es único
8a Para cada a en K , a+a=a
8b Para cada a en K , a.a=a
9a Para cada a en K , a+1=1 Propiedad de unicidad
9b Para cada a en K , a.0=0 Propiedad de cero
10a Para todos a y b en K , a+a.b=a
10b Para todos a y b en K , a.(a+b)=a
11 Para cada a en K , el inverso a' es único Unicidad de la inversión
12a Para todos a , b y c en K , a+(b+c)=(a+b)+c
12b Para todos a , b y c en K , a.(b.c)=(a.b).c
13a Para todos a y b en K, (a+b)'=a'.b'
13b Para todos a y b en K , (a.b)'=a'+b
14 Para cada a en K , ( a' )' = a Involución
Absorción
Asociatividad
Leyes de De Morgan
Unicidad de 0 y 1
Idempotencia
Conmutatividad
Distributividad
Axiomas de inversión
ÁLGEBRA DE BOOLE
Cierre
Se definen a
continuación:

18. Dos expresiones booleanas, E1 y E2 , se dicen que son
equivalentes (es decir, E1 = E2 ) cuando, ante las mismas
entradas, provocan las mismas salidas. Esto se puede
comprobar a partir de la tabla de verdad, o bien, partiendo de
una de ellas y aplicar álgebra de Boole, hasta llegar a la otra.
Equivalencia de expresiones booleanas
Ejemplo: Demostrar que E1 = E2 , donde:
hgfehgfdhgfchbaE ...........1 
hgfedcbaE .)...).((2 
¿es práctico usar la tabla de verdad
para comprobarlo en este caso?

19. Una función lógica presenta una correspondencia “uno a uno”
con un circuito lógico o con una tabla de verdad.
Correspondencia de la lógica combinacional
dcacbaz ).().( 
a
b
c
d
ba 
cba ).( 
ca 
d dca ).( 
z
c
CIRCUITO LÓGICO
a
b
c
d
ba 
cba ).( 
ca 
d dca ).( 
z
c
CIRCUITO LÓGICO
a
b
c
d
ba 
cba ).( 
ca 
d dca ).( 
z
c
CIRCUITO LÓGICO
Sea la siguiente función
lógica:
el circuito lógico y su tabla
de verdad serán:

20. Representación de un sistema
combinacional
Introducción
Los circuitos de Lógica Combinacional se caracterizan
porque sus salidas se definen por una combinación lógica de
sus entradas.

21. Minitérminos
Una función combina-
cional distintiva son los
minitérminos de “n”
variables, y se los
denota como mi. Son
funciones booleanas
cuya tabla de verdad
tiene un “1” en la
i-ésima fila, y un “0”
en las restantes. 43214 xxxxm 
432113 xxxxm 
A B C D .... m3 m4 ....
0 0 0 0 0 .... 0 0 ....
1 0 0 0 1 .... 0 0 ....
2 0 0 1 0 .... 0 0 ....
3 0 0 1 1 .... 1 0 ....
4 0 1 0 0 .... 0 1 ....
5 0 1 0 1 .... 0 0 ....
6 0 1 1 0 .... 0 0 ....
7 0 1 1 1 .... 0 0 ....
8 1 0 0 0 .... 0 0 ....
9 1 0 0 1 .... 0 0 ....
10 1 0 1 0 .... 0 0 ....
11 1 0 1 1 .... 0 0 ....
12 1 1 0 0 .... 0 0 ....
13 1 1 0 1 .... 0 0 ....
14 1 1 1 0 .... 0 0 ....
15 1 1 1 1 .... 0 0 ....
MINITÉRMINOS
nº
Entradas

22. Forma canónica “Suma de minitérminos”
Dada una función z de “n” variables, cuya tabla de verdad
tiene “1” en las filas a, b, ..., k, y “0” en las demás. A partir de
la definición de minitérmino, y usando la función OR, es
evidente que:
z = ma + mb + ... + mk
Ejemplo: Sean las funciones para z1=Z1(A,B,C,D),
z2=Z2(A,B,C,D) y z3=Z3(A,B,C,D), caracterizadas por la
siguiente tabla de verdad, determinar las funciones booleanas
correspondientes:

23. Forma canónica “Suma de minitérminos”
Solución: Aplicando el concepto de
minitérminos, las funciones busca-
das serán:
A B C D z1 z2 z3
0 0 0 0 0 1 1
0 0 0 1 0 1 1
0 0 1 0 0 0 1
0 0 1 1 0 0 0
0 1 0 0 0 0 1
0 1 0 1 0 0 0
0 1 1 0 1 1 1
0 1 1 1 1 1 0
1 0 0 0 0 0 1
1 0 0 1 0 0 0
1 0 1 0 1 1 1
1 0 1 1 1 1 0
1 1 0 0 0 0 1
1 1 0 1 0 0 0
1 1 1 0 1 1 1
1 1 1 1 1 1 0
ENTRADA SALIDAS
TABLA DE VERDAD
dabcdcabdcbadcba
dbcadcbadcbadcbadcbaz
abcddabccdba
dcbabcdadbcadcbadcbaz
abcddabccdbadcbabcdadbcaz





3
2
1

24. Construcción algebraica
Cualquier expresión booleana puede convertirse a su forma
canónica “suma de minitérminos” empleando las propieda-
des del álgebra de Boole. A esta forma canónica también suele
denominarse “Suma De Productos (SDP)”.
Ejemplo: Encontrar la forma canónica “suma de
minitérminos” de:
cbacbcaz 
Solución:          ddcbaddcbaaddcbbaz 
dcbadcbadcbadcbadcbadcbadcbadcbaz 
o bien:

25. Maxitérminos
Una segunda función son los
maxitérminos de “n” variables,
denotada como Mi. Son
funciones booleanas cuya tabla
de verdad tiene un “0” en la i-
ésima fila, y un “1” en las
restantes.
43213 xxxxM 
43214 xxxxM 
A B C D .... M3 M4 ....
0 0 0 0 0 .... 1 1 ....
1 0 0 0 1 .... 1 1 ....
2 0 0 1 0 .... 1 1 ....
3 0 0 1 1 .... 0 1 ....
4 0 1 0 0 .... 1 0 ....
5 0 1 0 1 .... 1 1 ....
6 0 1 1 0 .... 1 1 ....
7 0 1 1 1 .... 1 1 ....
8 1 0 0 0 .... 1 1 ....
9 1 0 0 1 .... 1 1 ....
10 1 0 1 0 .... 1 1 ....
11 1 0 1 1 .... 1 1 ....
12 1 1 0 0 .... 1 1 ....
13 1 1 0 1 .... 1 1 ....
14 1 1 1 0 .... 1 1 ....
15 1 1 1 1 .... 1 1 ....
MAXITÉRMINOS
nº
Entradas

26. Forma canónica “Producto de maxitérminos”
Toda función z tiene un conjunto único de maxitérminos Mi,
que corresponde al conjunto de ceros que aparecen en la
columna de salida de su tabla de verdad. La forma canónica
de producto de maxitérminos será la función AND o producto
lógico de estos maxitérminos. A esta forma canónica también
suele denominarse “Producto De Sumas (PDS)”.
Ejemplo: Sea la la siguiente función booleana de tres
variables: cbaz 
la expresión canónica de producto de maxitérminos será:
   cbacbacbaMMMz  654

27. Circuitos combinacionales
Las formas canónicas anteriores se representan con circuitos
combinacionales de dos niveles de compuertas:
S
U
M
A
P
R
O
D
U
C
T
O
S
DE
P
R
O
D
U
C
T
O
S
U
M
A
S
DE

28. Notación decimal
Las funciones boo-
leanas, dadas en
cualesquiera de sus
formas canónicas,
pueden escribirse de
manera simplificada
usando el símbolo 
para indicar la suma
de productos, y 
para el producto de
sumas.

29. Formas de dos niveles
La profundidad de un circuito se mide por el máximo número
de compuertas que una señal tiene que atravesar desde la
entrada hasta la salida.
Las formas canónicas vistas tienen una profundidad de dos,
considerando que se dispone de las entradas necesarias
complementadas.
A pesar de que suelen ser los circuitos más rápidos que
pueden lograrse con este tipo de implementación, esta
disposición no implica ser la mejor desde el punto de vista
del número de compuertas empleadas.

30. Formas de dos niveles
Los tres circuitos
tienen la misma
tabla de verdad.