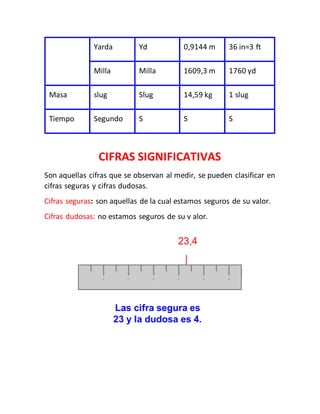
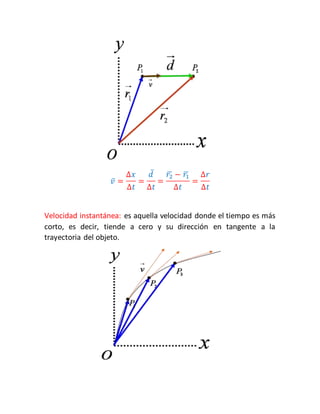
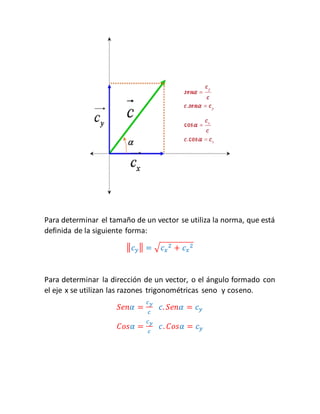
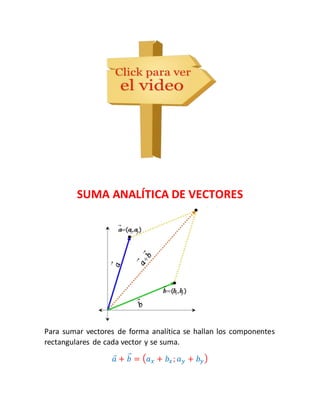
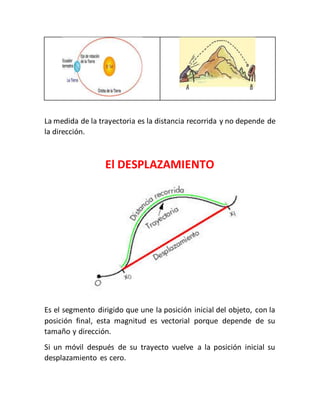
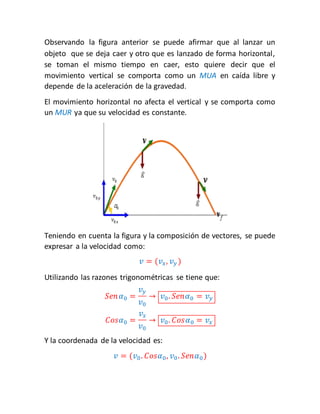
Este documento introduce conceptos básicos de física como magnitudes físicas, sistemas de unidades, vectores y su suma, y tipos de movimiento. Explica que las magnitudes pueden ser escalares o vectoriales, y describe el sistema internacional de unidades. Además, resume los tipos básicos de movimiento como movimiento rectilíneo uniforme, sistemas de referencia, y conceptos como desplazamiento, velocidad y aceleración.

1. U
INTRODUCCIÓN A LA FÍSICA
MAGNITUDES FÍSICAS
MÚLTIPLOS Y SUBMÚLTIPLOS
CONVERSIÓN DE MEDIDAS
MAGNITUDES ESCALARES Y VECTORIALES
VECTOR DESPLAZAMIENTO Y VELOCIDAD
SUMA GRÁFICA DE VECTORES
COMPONENTES DE UN VECTOR
SUMA ANALÍTICA DE VECTORES
EL MOVIMIENTO
SISTEMAS DE REFERENCIA
CUERPOS PUNTUALES

2. OS NATU
TRAYECTORIA Y DISTANCIA RECORRIDA
DESPLAZAMIENTO
RAPIDEZ
MOVIMIENTO RECTILÍNEO UNIFORME
MOVIMIENTO UNIFORME ACELERADO
CAÍDA LIBRE
MOVIMIENTO DE PROYECTILES

3. INTRODUCCIÓN A LA FÍSICA
MAGNITUDES FÍSICAS
Para describir un sistema físico es necesario la medición, ya que esta
permite establecer relaciones cuantitativas entre las diversas
variables que intervienen en su comportamiento.
Cuando una propiedad caracteriza a los cuerpos o fenómenos
naturales y puede ser medida se le llama magnitud física.
Algunas como: la masa, la velocidad, la longitud, tiempo,
temperatura, etc. Otras propiedades como: el olor, la bondad, la
belleza, etc. no son magnitudes físicas.
Magnitud fundamental: Son aquellas que son independientes de los
demás como: longitud, masa, tiempo, intensidad de corriente,
temperatura, cantidad de sustancia e intensidad luminosa.

4. Magnitud derivada: Son aquellas que están compuestas por dos o
más magnitudes elementales como la velocidad que se expresa en
unidades de longitud sobre tiempo (km/h).
SISTEMA INTERNACIONAL DE MEDIDAS (SI).
Para medir las magnitudes físicas se utilizan patrones llamados
unidades, que y se basan en cantidades conocidas.
En 1960, la conferencia general de Pesos y Medida, se creó un
acuerdo conformado por científicos e ingenieros de diferentes
partes del mundo y establecieron el sistema internacional de
medidas.
MAGNITUD UNIDAD SÍMBOLO
Longitud metro m

5. Masa kilogramo kg
Tiempo segundo s
Intensidad
de corriente
Amperio A
Temperatura Kelvin K
Cantidad de
sustancia
mol mol
Intensidad
luminosa.
candela cd
Aquellas unidades que reciben un nombre en honor a un científico
se expresan en letras mayúsculas, como: Kelvin (K), Newton (N),
Pascal (PA), Ampere (A), etc.

6. MÚLTIPLOS Y SUBMÚLTIPLOS
En ocasiones a la hora de expresar una medida de gran tamaño como
la distancia al sol en metros o de un tamaño muy pequeño el peso
de un electrón, es más conveniente utilizar los múltiplos y
submúltiplos del sistema internacional de medidas.

7. Para convertir de múltiplos y submúltiplos a una unidad patrón se
tiene en cuenta la regla de 3 simple.
Ejemplo: Expresar 6m en am.
1푎푚 10−18푚
푥 6푚

8. Se realiza:
푥 =
(6푚)(1푎푚)
10−18푚
=
(6)(1푎푚)
10−18 = 6 × 1018푎푚
Para convertir de múltiplos a submúltiplos o viceversa se cuentan
los espacios que hay entre ellos y se aplica la regla de 3 simple:
Ejemplo: Expresar 12 cm en Tm.
1푇푚 1014푐푚
푥 12푐푚
Se realiza:
푥 =
(12푐푚)(1푇푚)
1014푐푚
=
(12)(푇푚)
10−18 = 12 × 10−14푇푚
SISTEMA INGLÉS O BRITÁNICO
Existen otros sistemas de medición como el sistema inglés, lo usan
países de la comunidad inglesa o que fueron, este sistema va en
desuso debido a que la comunidad científica ya casi no lo utiliza.
También se puede hablar de magnitudes, unidad, y símbolo y se
pueden expresar en términos del sistema internacional de medidas.
Magnitud Unidad Símbolo SI Inglés
Longitud
Pie Ft 0,3048 m 12 in
Pulgada In 0,0254 m 1 in

9. Yarda Yd 0,9144 m 36 in=3 ft
Milla Milla 1609,3 m 1760 yd
Masa slug Slug 14,59 kg 1 slug
Tiempo Segundo S S S
CIFRAS SIGNIFICATIVAS
Son aquellas cifras que se observan al medir, se pueden clasificar en
cifras seguras y cifras dudosas.
Cifras seguras: son aquellas de la cual estamos seguros de su valor.
Cifras dudosas: no estamos seguros de su v alor.

10. MAGNITUDES ESCALARES Y VECTORIALES
Una magnitud es una propiedad de los cuerpos que puede ser
medida, como el tamaño, el peso la velocidad entre otras.
Estas magnitudes se pueden clasificar en:
Magnitudes escalares: son aquella que no dependen de una
dirección como: el tiempo, la masa, la rapidez, la distancia recorrida,
la densidad, etc.
Magnitudes vectoriales: son aquellas que dependen de una dirección
como: el desplazamiento, la velocidad, la aceleración, la fuerza, etc.
Las magnitudes vectoriales son representadas por medio de un
vector, que es un segmento dirigido cuya longitud es proporcional a
la medida que representa.
Todos los vectores se denotan con una letra y en arriba de esta una
flecha y se representan en el plano cartesiano y en el espacio.
Todo vector tiene una dirección y una norma:

11. Dirección: es el ángulo formado entre el vector y el eje de las “x”.
Norma: es un número positivo que representa el tamaño del vector.
La norma de un vector se representa la letra sin flechas o dentro
de barras.
Cuando dos vectores tienen la misma norma y la misma dirección
se dice que estos vectores son iguales.

12. VECTOR DESPLAZAMIENTO
El vector desplazamiento describe una línea recta desde la posición
inicial de un objeto hasta la posición final de este.
VECTOR VELOCIDAD
El vector velocidad es la magnitud que mide que tan aprisa ha
cambiado el vector posición en un intervalo de tiempo dado.
Velocidad media: en el movimiento uniforme acelerado se tiene que
la velocidad media es:
푣̅ =
Δ푥
Δ푡
En el plano cartesiano se puede expresar como:

13. 푣̅ =
Δ푥
Δ푡
=
푑̅
Δ푡
=
푟̅2 − 푟̅1
Δ푡
=
Δ푟
Δ푡
Velocidad instantánea: es aquella velocidad donde el tiempo es más
corto, es decir, tiende a cero y su dirección en tangente a la
trayectoria del objeto.

14. La norma de la velocidad instantánea es llamada rapidez y su
dirección es la tangente de la trayectoria en cada punto.
SUMA GRÁFICA DE VECTORES
La suma gráfica de vectores se puede realizar de dos maneras.
Cabeza y cola: Se unen las cabezas y las colas de cada vector y el
resultado es unir la cola y la cabeza del último vector.
Método del paralelogramo: Este método permite solamente sumar
vectores de dos en dos. Consiste en disponer gráficamente los dos
vectores de manera que los orígenes de ambos coincidan en un
punto, trazando rectas paralelas a cada uno de los vectores, en el
extremo del otro y de igual longitud, formando así un paralelogramo.

15. COMPONENTES DE UN VECTOR
Todo vector tiene sus componentes relacionados con los ejes del
plano cartesiano. Los componentes del vector 푐̅= (푐̅푥, ̅푐̅푦̅).

16. Para determinar el tamaño de un vector se utiliza la norma, que está
definida de la siguiente forma:
‖푐푦 ‖ = √푐푥
2 + 푐푥
2
Para determinar la dirección de un vector, o el ángulo formado con
el eje x se utilizan las razones trigonométricas seno y coseno.
푆푒푛훼 =
푐푦
푐
푐. 푆푒푛훼 = 푐푦
퐶표푠훼 =
푐푦
푐
푐. 퐶표푠훼 = 푐푦

17. SUMA ANALÍTICA DE VECTORES
Para sumar vectores de forma analítica se hallan los componentes
rectangulares de cada vector y se suma.
푎⃑ + 푏⃑⃑ = (푎푥 + 푏푥 ; 푎푦 + 푏푦 )

18. EL MOVIMIENTO

19. El movimiento es el cambio de posición de un objeto con respecto a
un observador físico, La ciencia que estudia el movimiento es la
cinemática y se encarga de analizar las magnitudes que lo involucran.
Para estudiar el movimiento se debe de tener en cuenta dos
conceptos primordiales.
SISTEMAS DE REFERENCIA
Un sistema de referencia es un punto en el espacio del cual partimos
para una magnitud a un objeto en reposo o en movimiento en un
instante dado.
Para distancia se tienen tres tipos de sistemas de referencia
dependiendo de las dimensiones necesarias para describir el
movimiento:
o Una dimensión - Movimientos Lineales.
o Dos dimensiones - Movimientos en el Plano.
o Tres dimensiones - Movimientos en el Espacio.
El reloj es el sistema de referencia para el tiempo, en conclusión, el
estudio del movimiento de un objeto depende del sistema de
referencia ya que puede variar el valor de la trayectoria, posición o
la velocidad.

20. CUERPOS PUNTUALES
Es una representación en forma de punto para el estudio del
movimientos de objetos sin importar si es de tamaño micro o macro.
TRAYECTORIA Y DISTANCIA RECORRIDA
Es el recorrido que describe un objeto durante su movimiento, esta
trayectoria puede ser:
Rectilínea: cuando su trayectoria es una línea recta.
Curvilíneo: Cuando su trayectoria describe una línea curva, y pueden
ser:
Curvilíneo: Cuando su
trayectoria describe una línea
curva, y pueden ser:
Circular
Elíptico Parabólico

21. La medida de la trayectoria es la distancia recorrida y no depende de
la dirección.
El DESPLAZAMIENTO
Es el segmento dirigido que une la posición inicial del objeto, con la
posición final, esta magnitud es vectorial porque depende de su
tamaño y dirección.
Si un móvil después de su trayecto vuelve a la posición inicial su
desplazamiento es cero.

22. RAPIDEZ
Es la distancia recorrida en un determinado tiempo, la rapidez es una
magnitud escalar es decir, no depende de la dirección. La rapidez
media es la distancia recorrida de un móvil sobre el tiempo
empleado. Cuando se habla de rapidez en diferentes intervalos es
muy probable que haya variado en algún instante del intervalo, para
eso se calcula la rapidez instantánea.
MOVIMIENTO RECTILÍNEO UNIFORME
Cuando un cuerpo se mueve en línea recta y su velocidad
instantánea no cambia es decir es constante, se le llama movimiento
rectilíneo uniforme.
Como la velocidad instantánea es la misma en cada instante de
tiempo, es también igual a la velocidad media que se expresa como:
푣 =
Δ푥
Δ푦
=
푥 − 푥0
푦 − 푦0

23. Este movimiento se puede representar gráficamente con respecto al
tiempo, espacio- tiempo, velocidad-tiempo.
푚 =
Δ푥
Δ푡
=
푥 − 푥0
푡
= 푣
La grafica del espacio con respecto al tiempo es una función lineal
cuya pendiente es la velocidad y el corte en y es la posición inicial del
objeto. Ya que es una función lineal se puede expresar como tal
utilizando la ecuación de la posición del movimiento rectilíneo
uniforme (MRU).
Δ푥 = 푣. 푡
푥 − 푥0 = 푣. 푡
푥 = 푣. 푡 + 푥0
La grafica de la velocidad con respecto al tiempo es una función
constante, ya que la velocidad no varía en ningún momento, el área
definida bajo la curva hasta la horizontal es el valor del cambio de
posición y está definida como:
Δ푥 = 푣. 푡

24. Ejemplo:
¿Qué distancia recorre un ciclista que se mueve durante 30 min con
velocidad constante de 10m/s?
Se organizan los datos obtenidos.
Se expresan los datos en las mismas unidades de medida.
Δ푥 =? 푡 = 30푚푖푛 푣 = 10 푚
⁄푠
30푚푖푛.
60푠
1푚푖푛
= 1800푠
Se reemplaza en la ecuación del desplazamiento de MRU.
Δ푥 = 푣. 푡
Δ푥 = (10 푚
⁄푠)(1800푠)
Δ푥 = 18.000푚

25. MOVIMIENTO RECTILÍNEO VARIADO
Este movimiento también llamada MOVIMIENTO UNIFORME
ACELERADO (MUA) se presenta cuando hay un cambio de velocidad
en un tiempo determinado y presenta una aceleración o una
desaceleración.
Cuando cambia su velocidad de menor a mayor su aceleración es
positiva, cuando cambia de mayor a menor (desacelera) su
aceleración es negativa.
Como la aceleración es el cambio de la velocidad en un tiempo
transcurrido se puede expresar como:
푎 =
Δ푣
Δ푡
=
푣푓 − 푣0
푡푓 − 푡0
Si se tiene en cuenta que las medidas del tiempo hechas con el
cronómetro empiezan desde cero.

26. 푎 =
푣푓 − 푣0
푡
La representación gráfica de un MUA es:
De la gráfica de velocidad tiempo, se puede expresar el cambio de la
posición como el área comprendida bajo la función lineal y la
horizontal, se puede determinar que:
Δ푥 = 퐴1 + 퐴2 =
(푣푓 − 푣0 )푡
2
+ 푣0 푡 =
(푣푓 푡 − 푣0 푡)
2
+ 푣0 푡
Δ푥 =
푣푓 푡
2
−
푣0 푡
2
+ 푣0 푡 =
푣푓 푡
2
+
−푣0 푡 + 2푣0 푡
2
=
푣푓푡
2
+
푣0 푡
2
Teniendo en cuenta que:
푎 =
푣푓 − 푣0
푡
Se despeja 푣푓 .
푎 =
푣푓 −푣0
푡
푎푡 = 푣푓 − 푣0 푎푡 + 푣0 = 푣푓
Y se reemplaza en:

27. Δ푥 =
푣푓 푡
2
+
푣0 푡
2
=
(푎푡 + 푣0 )푡
2
+
푣0 푡
2
=
푎푡2
2
+
푣0 푡
2
+
푣0 푡
2
Δ푥 =
푎푡2
2
+
2푣0 푡
2
=
푎푡2
2
+ 푣0 푡
Esta es la ecuación del desplazamiento con respecto al tiempo,
despejando el tiempo en:
푎 =
푣푓 − 푣0
푡
→ 푎푡 = 푣푓 − 푣0 → 푡 =
푣푓 − 푣0
푎
Reemplazándola en la ecuación del desplazamiento, se obtiene:
Δ푥 =
푎푡2
2
+ 푣0 푡 =
푎 (
푣푓 − 푣0
푎
2
)
2
+ 푣0 (
푣푓 − 푣0
푎
)
Δ푥 =
푎
(푣푓 − 푣0 )
2
푎2
2
푣푓 − 푣0
+ 푣0 (
푎
)
Δ푥 =
푣푓
2 − 2푣푓푣0 + 푣0
2
2푎
+
푣푓 푣0 − 푣0
2
푎
Δ푥 =
푣푓
2 − 2푣푓푣0 + 푣0
2 + 2푣푓 푣0 − 2푣0
2
2푎
=
푣푓
2 − 푣0
2
2푎
En conclusión las ecuaciones del MUA son:
푎 =
푣푓 − 푣0
푡
Δ푥 =
푎푡2
2
+ 푣0 푡 Δ푥 =
푣푓
2 − 푣0
2
2푎
Ejemplo: una persona que va a cruzar la calle viene corriendo a una
velocidad de 4 m/s, cuando observa que el semáforo que está
ubicado a 2 metros cambia de rojo a verde y disminuye su velocidad

28. y se detiene justo al lado del semáforo. ¿Hallar la aceleración y el
tiempo de la persona?
Se organizan los datos y se colocan los datos en las mismas unidades.
푣0 = 4 푚
⁄푠 푣푓 = 0 푚
⁄푠 Δ푥 = 2푚 푡 =? 푎 =?
Se despeja la formula para hallar la aceleración de la persona.
Δ푥 =
푣푓
2 − 푣0
2
2푎
→ 푎Δ푥 =
푣푓
2 − 푣0
2
2
→ 푎 =
푣푓
2 − 푣0
2
2Δ푥
Se reemplazan los valores, sin omitir las unidades de estos.
푎 =
(0 푚
⁄푠)2 − (4 푚
⁄푠)2
2(2푚)
=
−16 푚2
푠2 ⁄
4푚
= −4 푚
⁄푠2
Se despeja la formula para hallar el tiempo de la persona.

29. 푎 =
푣푓 − 푣0
푡
→ 푎푡 = 푣푓 − 푣0 → 푡 =
푣푓 − 푣0
푎
Se reemplazan los valores, sin omitir las unidades de estos.
푡 =
푣푓 − 푣0
푎
=
(0 푚
⁄푠) − (4 푚
⁄푠)
(−4 푚
⁄푠2)
=
−(4 푚
⁄푠)
−4 푚
⁄푠2
= 1푠

30. CAÍDA LIBRE
Aristóteles estableció que los objetos caían según el peso de estos,
es decir, los objetos de mayor peso caían más rápido que los de
menor peso.
200 años después Galileo
Galilei, refutó la teoría
aristotélica sobre la caída
de los cuerpos. Utilizando
planos inclinados de
pequeña pendiente,
arrojando esferas de
diferente masa por las
m1
m2
m1 > m2
pendientes demostró que cuando las esferas cuando pasaban de un
determinado peso y la resistencia del aire es despreciable, estas
hacían su recorrido en el mismo tiempo.
Por medio de estos planos inclinados también demostró que los
cuerpos presentaban una aceleración constante bajo el empuje de la
gravedad y refutó otra de las teorías de Aristóteles que decía que
para mantener un cuerpo en movimiento constante, se debía aplicar
una fuerza continua, esto lo demostró explicando que si un objeto se
deslizaba por una superficie supremamente lisa esta se movería en
velocidad constante.
Galileo Galilei, demostró a sus estudiantes que dos objetos
independientemente de su peso caían al mismo tiempo,
arrojandolos desde la torre de Pisa. Cuando un cuerpo se deja caer
en el vacío este experimenta una aceleración constante que
depende de la fuerza de atracción que le ejerce la tierra hacia su
centro, esta aceleración se denomina aceleración gravitacional y se

31. denota con la letra “g”. Se ha demostrado experimentalmente que
el valor aproximado de la aceleración gravitacional es de:
9.8 푚
⁄푠2
g>0 g<0
Este valor de la gravedad no depende del movimiento inicial, es
decir, que para un objeto que se deja caer o es lanzado hacia arriba
o hacia abajo el valor de la gravedad es el mismo aunque si varía su
dirección.
La caída libre se puede considerar un movimiento uniforme
acelerado (MUA) si se tiene en cuenta que:
● Que la resistencia al aire es despreciable.

32. ● Que la gravedad no cambia con la altitud.
Las ecuaciones de caída libre son similares a las de (MUA), solo se
cambia la variable “x” que es distancia horizontal, por la variable “y”
que es distancia vertical y la variable “a” que es aceleración por la
variable “g ” que es aceleración gravitacional. Cuando se le induce
una velocidad inicial se llama “caída no libre”.
Las ecuaciones de caída libre son:
푔 =
푣푓 − 푣0
푡
Δ푦 =
푔푡2
2
+ 푣0 푡 Δ푦 =
푣푓
2 − 푣0
2
2푔
A la hora de solucionar problemas de caída libre se debe tener en
cuenta:
1. Ordenar los datos que se tienen y los que faltan.
2. Buscar la ecuación que nos permita hallar alguno de los datos que
nos faltan y despejarse antes de reemplazar.
Ejemplo: Un objeto se deja caer desde una altura de 25m.
a) Hallar la velocidad final con que golpea el suelo la pelota.
b) Hallar el tiempo que se demora la pelota en tocar el suelo.
Solución:
Se organizan los datos.

33. 푣0 = 0 푚
⁄푠 푣푓 =? Δ푦 = 25푚 푡 =? 푔 = 9.8 푚
⁄푠2
Se despeja la formula para hallar la velocidad con que el objeto llega
al suelo.
Δ푦 =
푣푓
2 − 푣0
2
2푔
→ 2푔. Δ푦 = 푣푓
2 − 푣0
2 → 2푔. Δ푦 + 푣0
2 = 푣푓
2
√2푔. Δ푦 + 푣0
2 = 푣푓
Se reemplazan los valores, sin omitir las unidades de estos.
푣푓 = √2푔. Δ푦 + 푣0
2 = √2 (9.8 푚
⁄푠2) . (25푚) + (0 푚
⁄푠)2
⁄푠2) . (25푚) = √490 푚2
푣푓 = √2 (9.8 푚
⁄푠2 = 22.14 푚
⁄푠
La velocidad con que el objeto llega al suelo es de 22.14 m/s.
Se despeja la formula para hallar el tiempo del objeto llegar al suelo.
푔 =
푣푓 − 푣0
푡
→ 푔푡 = 푣푓 − 푣0 → 푡 =
푣푓 − 푣0
푔
Se reemplazan los valores, sin omitir las unidades de estos.
푡 =
푣푓 − 푣0
푔
=
(22.14 푚
⁄푠) − (0 푚
⁄푠)
(9.8 푚
⁄푠2)
=
(22.14 푚
⁄푠)
(9.8 푚
⁄푠2)
= 2.26푠
El tiempo que se demora en caer el objeto al piso es de 2.26s.

34. MOVIMIENTO DE PROYECTILES
Este movimiento está conformado por la composición de dos
movimientos, uno vertical y el otro horizontal.

35. Observando la figura anterior se puede afirmar que al lanzar un
objeto que se deja caer y otro que es lanzado de forma horizontal,
se toman el mismo tiempo en caer, esto quiere decir que el
movimiento vertical se comporta como un MUA en caída libre y
depende de la aceleración de la gravedad.
El movimiento horizontal no afecta el vertical y se comporta como
un MUR ya que su velocidad es constante.
Teniendo en cuenta la figura y la composición de vectores, se puede
expresar a la velocidad como:
푣 = (푣푥, 푣푦 )
Utilizando las razones trigonométricas se tiene que:
푆푒푛 훼0 =
푣푦
푣0
→ 푣0 . 푆푒푛훼0 = 푣푦
퐶표푠훼0 =
푣푥
푣0
→ 푣0 . 퐶표푠훼0 = 푣푥
Y la coordenada de la velocidad es:
푣 = (푣0 . 퐶표푠훼0 , 푣0 . 푆푒푛훼0 )

36. Considerando que donde inicia el movimiento parabólico es en el
origen, es decir, en la coordenada (0,0), entonces:
Movimiento horizontal Movimiento vertical
푣푥 =
Δ푥
푡
푔 =
푣푓푦 − 푣0푦
푡
Δ푦 =
푔푡2
2
+ 푣0푦 푡
Δ푦 =
푣푓푦
2 − 푣0푦
2
2푔
Ejemplo: Un balón es pateado a una velocidad de 20m/s en un
ángulo con respecto a la horizontal de 45º.
a) Calcular las componentes de la velocidad inicial.
Componente en x Componente en y
푣푥 = 푣0 . 퐶표푠훼0
푣푥 = (20 푚
⁄푠).퐶표푠45°
푣푥 = (20 푚
⁄푠). (0.71)
푣푥 = 14.14 푚
⁄푠
푣0푦 = 푣0 . 푆푒푛 훼0
푣0푦 = (20 푚
⁄푠).푆푒푛45°
푣0푦 = (20 푚
⁄푠). (0.71)
푣0푦 = 14.14 푚
⁄푠
b) Hallar las componentes de la velocidad cuando t=0,6 s .
Componente en “x”, t= 0,6s
Como la velocidad en el eje “x” es uniforme tiene la misma velocidad
en cualquier tiempo.
푣푥 = 14.14 푚
⁄푠
Componente en “y”, t= 0.6s
Se despeja la formula.
푔 =
푣푓푦 − 푣0푦
푡
→ 푔푡 = 푣푓푦 − 푣0푦 → 푔푡 + 푣0푦 = 푣푓푦

37. Se reemplazan los valores.
푣푓푦 = 푔푡 + 푣0푦 = (9.8 푚
⁄푠2)(0.6푠) + (14.14 푚
⁄푠) = 8.14 푚
⁄푠
c) Calcular la distancia recorrida y la altura del balón en t=0.6s.
Se despeja la formula.
푣푥 =
Δ푥
푡
→ 푣푥 . 푡 = Δ푥
Se reemplazan los valores.
Δ푥 = 푣푥 . 푡 = (14.14 푚
⁄푠). (0.6푠) = 8.48푚
d) Calcular la altura máxima que alcanza el balón.
Cuando el balón alcanza la altura máxima 푣푓푦 = 0 푚
⁄푠.
Se reemplazan los valores en la formula.
Δ푦 =
푣푓푦
2 − 푣0푦
2
2푔
=
(0 푚
⁄푠)2 − (14.14 푚
⁄푠)2
2(−9.8 푚
⁄푠2)
=
⁄푠2
−199.94 푚
−19.6 푚
⁄푠2)
Δ푦 = 10푚
e) Calcular la distancia máxima que alcanza el balón.
El tiempo que se demora en subir el balón es el mismo tiempo que
se demora en bajar.
Se halla el tiempo que se demora en alcanzar la altura máxima.
Se despeja la formula.
푔 =
푣푓푦 − 푣0푦
푡
→ 푔푡 = 푣푓푦 − 푣0푦 → 푡 =
푣푓푦 − 푣0푦
푔
Se reemplazan los valores.

38. 푡 =
(0 푚
⁄푠) − (14.14 푚
⁄푠)
(−9.8 푚
⁄푠2)
=
−14.14 푚
⁄푠
−9.8 푚
⁄푠2
= 1.41푠
El tiempo que se demora en subir el balón es el mismo tiempo que
se demora en bajar, el tiempo del alcance máximo es de 푡 = 2.82푠
Se halla el alcance máximo despejando la formula.
푣푥 =
Δ푥
푡
→ 푣푥 . 푡 = Δ푥
Se reemplazan los valores.
Δ푥 = 푣푥. 푡 = (14.14 푚
⁄푠)(2.82푠) = 39.87푚

39. BIBLIOGRAFÍA
 Richard Stallman. Enciclopedia universal. 1999. disponible en:
www.wikipedia.com
 Juan Carlos Fernández Gordillo. Matemáticas. Valencia España.
Edifesa, Disponible en: www.vitutor.com
 Chad Hurley. Steve Chen. Jawed Karim. Reproductor de video
online. 15 de febrero de 2005. Disponible en
http://www.youtube.com
 Cesar Aurelio Herreño. Energia I. Ed. Voluntad. 2006
 Iván Antonio Morales Ferrero. Esperanza del Pilar Infante Luna. Física I.
Ed Norma. 2007.
SOFTWARE
 Kvisoft Inc. FlipBook Maker Pro. 2014. Disponible en:
www.kvisoft.com/flipbook-maker-pro
 Diego Uscanga. aTube Catcher.2011. Disponible en:
www.atubecatcher.es
VIDEOS
 licamu. Introducción a la física. 2010. Disponible en:
https://www.youtube.com/watch?v=dr7r7xSMUYA
 Camilo Alfonso. Magnitudes físicas. 2011. Disponible en:
https://www.youtube.com/watch?v=IyRC44rDzR8

40.  Humberto Higinio. Entendiendo los múltiplos y sub múltiplos-parte.
2011. Disponible en:
https://www.youtube.com/watch?v=2xUpBEj0az8
 Julio Alberto Ríos Gallego. Conversión de unidades de rapidez.
2011. Disponible en:
https://www.youtube.com/watch?v=SkfXl_-vUY8
 Oliver Martínez. Magnitudes escalares y vectoriales. 2013.
Disponible en:
https://www.youtube.com/watch?v=S98y7k3lj6w
 Wiman enrique Pérez Benítez. Diferencia conceptos de
desplazamiento, trayectoria, velocidad y rapidez. 2011
Disponible en:
https://www.youtube.com/watch?v=u24VOT6gEWI
 Hernán puentes. Como sumar vectores en física- método
grafico- vectores- video 098. 2012. Disponible en:
https://www.youtube.com/watch?v=qvw7j9eKGdg
 Rubén Sebastián. Vectores: componentes cartesianas.2014.
disponible en:
https://www.youtube.com/watch?v=oYobFDvpo0Q
 Juan Carlos Velásquez Hernández. Suma y resta de vectores
método analítico. 2011. Disponible en:
https://www.youtube.com/watch?v=ycPw-c9kkZQ
 Harvey Hernández. Concepto de movimiento. 2014 disponible
en: https://www.youtube.com/watch?v=Jan9oc8X_zY
 Víctor Hugo morales. Física: marco de referencia y sistemas de
coordenadas. 2012. Disponible en:
https://www.youtube.com/watch?v=BmKLzaj2REo
 Cinematik3D. cinemática 3D trayectoria, distancia y
desplazamiento. 2014. Disponible en:
https://www.youtube.com/watch?v=kXa3BRRdIH8

41.  Hecmy Carolina. Movimiento rectilíneo uniforme.2009
disponible en:
https://www.youtube.com/watch?v=ywQRN29OL38
 Eusebio Molina Rodríguez. Movimiento rectilíneo
uniformemente acelerado (Análisis e interpretación gráfica). 2013.
Disponible en: https://www.youtube.com/watch?v=5ZXN53KI_as
 Atanael Varela López. Tiro vertical y caída libre. 2012. Disponible
en: https://www.youtube.com/watch?v=yZKFeakgn3A
 Ricardo Gutiérrez. Movimiento de proyectiles. 2009. Disponible en:
https://www.youtube.com/watch?v=QnwA3K2fgJ0