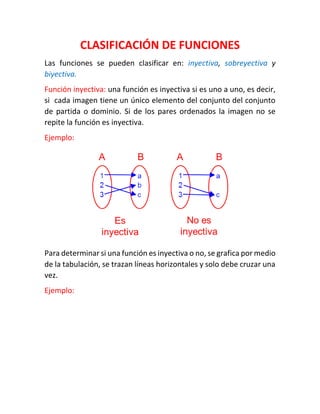
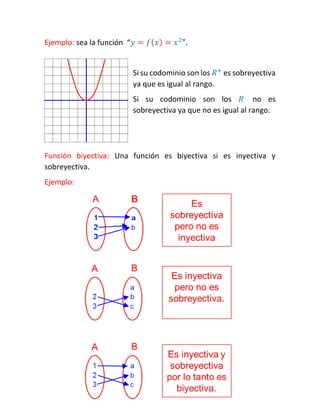
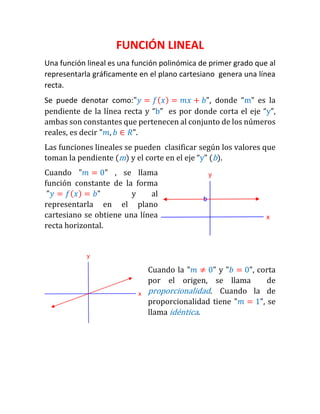
El documento trata sobre diferentes tipos de funciones matemáticas como funciones lineales, cuadráticas, exponenciales y sus características. Explica conceptos como dominio, codominio, rango e incluye ejemplos para ilustrar funciones crecientes, decrecientes, par e impar.

1. CONCEPTO DE RELACIÓN Y FUNCIÓN.
ELEMENTOS DE UNA FUNCIÓN.
CLASIFICACIÓN DE FUNCIONES.
FUNCIÓN PAR E IMPAR.
FUNCIÓN CRECIENTE, DECRECIENTE, CONSTANTE Y PERIÓDICA.
FUNCIÓN LINEAL.
FUNCIÓN LOGARÍTMICA.
FUNCIÓN EXPONENCIAL.
FUNCIÓN CUADRÁTICA
FUNCIÓN CÚBICA.
FUNCIÓN RACIONAL.
FUNCIÓN VALOR ABSOLUTO

2. FUNCIÓN A TROZOS.
OPERACIONES CON FUNCIONES.
FUNCIÓN PARTE ENTERA.
FUNCIÓN INVERSA

3. CONCEPTO DE RELACIÓN
Es una correspondencia entre los elementos de dos conjuntos llamados conjunto de partida y conjunto de llegada.
CONCEPTO DE FUNCIÓN
Es una relación donde los elementos del conjunto de partida le corresponden un único elemento del conjunto de llegada.

4. Las funciones se pueden denotar como "푦=푓(푥)", Donde "푥" es la variable independiente (se le asignan valores) y "푓(푥)" la dependiente (la que depende del valor asignado en la variable independiente).
La imagen de una función son los valores de la variable dependiente y se hallan encontrando el valor numérico de la función con los valores asignados a la variable dependiente.
Ejemplo: Hallar la imagen de "푦=푓(푥)=푥2+5푥+2" en los valores "푥=0,푥=−1,푥=3".
푦=푓(0)=(0)2+5(0)+2=0+0+2=2 푦=푓(−1)=(−1)2+5(−1)+2=1−5+2=−2 푦=푓(3)=(3)2+5(3)+2=9+15+2=26
Las imágenes del conjunto son "{2,−2,26}" , y su representación en un diagrama de Vens o sagital.
ELEMENTOS DE UNA FUNCIÓN
Dominio: Es el conjunto de valores que toma la variable independiente o el conjunto de partida.
Codominio: son los valores que puede tomar el conjunto de llegada o variable dependiente o imagen.

5. Rango: es el conjunto de valores que toma el conjunto de llegada o variable independiente o imagen.
Ejemplo: sea la función "퐹:퐴→퐵"
Dominio {1,2,3}
Codominio. {−2,4,5,10}
Rango {−2,4,5}

6. CLASIFICACIÓN DE FUNCIONES
Las funciones se pueden clasificar en: inyectiva, sobreyectiva y biyectiva.
Función inyectiva: una función es inyectiva si es uno a uno, es decir, si cada imagen tiene un único elemento del conjunto del conjunto de partida o dominio. Si de los pares ordenados la imagen no se repite la función es inyectiva.
Ejemplo:
Para determinar si una función es inyectiva o no, se grafica por medio de la tabulación, se trazan líneas horizontales y solo debe cruzar una vez.
Ejemplo:

7. Función Sobreyectiva: también llamada epiyectiva, si y sólo si cada elemento del conjunto de llegada es imagen de al menos un elemento de partida, es decir todos los elemento del conjunto de llegada están relacionados, o sea que el codominio es igual al rango.
Ejemplo:
Para determinar si una función es sobreyectiva o no, se halla el rango y el codominio, si son iguales es sobreyectiva si son diferentes no.se

8. Ejemplo: sea la función “푦=푓(푥)=푥2".
Si su codominio son los 푅+ es sobreyectiva ya que es igual al rango.
Si su codominio son los 푅 no es sobreyectiva ya que no es igual al rango.
Función biyectiva: Una función es biyectiva si es inyectiva y sobreyectiva.
Ejemplo:

9. Ejemplo:

10. FUNCIÓN PAR E IMPAR
Las funciones dependiendo de su simetría puede ser par o impar o ninguna de las dos.
Una función es par si se verifica que "푓(−푥)=푓(푥)", su simetría es con el eje vertical.
Ejemplo: Determinar si la función "푓(푥)=푥4+4푥2−3"
Se reemplaza "푥" por "−푥". 푓(−푥)=(−푥)4+4(−푥)2−3 푓(−푥)=푥4+4푥2−3 푓(−푥)=푓(푥)
La función es par.
Una función es impar si se verifica que "푓(−푥)=−푓(푥)", su simetría es con el origen de las coordenadas.
Ejemplo: Determinar si la función "푓(푥)=푥3−푥"
Se reemplaza "푥" por "−푥". 푓(−푥)=(−푥)3−(−푥) 푓(−푥)=−푥3+푥 푓(−푥)=−(푥3−푥) 푓(−푥)=−푓(푥)

11. FUNCIÓN CRECIENTE
Una función es creciente en un intervalo "[푎,푏]", si existen dos puntos de dicho intervalo "푥1", y "푥2" que cumplen con: 푥1<푥2→푓(푥1)<푓(푥2)
Ejemplo: Determinar si la función "푦=푓(푥)=푥2+3" es creciente en "[2,5]".
Se reemplazan dos valores que estén en el intervalo dado en la función. 푦=푓(3)=(3)2+3=12 푦=푓(4)=(4)2+3=19
Por lo tanto: 3<4→푓(3)<푓(4)
La función es creciente en el intervalo "[2,5]".

12. FUNCIÓN DECRECIENTE
Una función es decreciente en un intervalo "[푎,푏]", si existen dos puntos de dicho intervalo "푥1", y "푥2" que cumplen con: 푥1<푥2→푓(푥1)>푓(푥2)
Ejemplo: Determinar si la función "푦=푓(푥)=푥2+3" es creciente en "[−3,0]".
Se reemplazan dos valores que estén en el intervalo dado en la función. 푦=푓(−2)=(−2)2+3=7 푦=푓(−1)=(−1)2+3=4
Por lo tanto: −2<−1→푓(−2)>푓(−1)
La función es decreciente en el intervalo "[2,5]".
Una función es constante en un intervalo cuando no es creciente ni decreciente en este.
FUNCIÓN PERIÓDICA
Una función es periódica si cada determinado espacio se repiten las imágenes, es decir, cumple con "푓(푥+푡)=푓(푥)" , donde “t” es el periodo.
Ejemplo: Graficar "푦=푓(푥)=cos푥"

14. FUNCIÓN LINEAL
Una función lineal es una función polinómica de primer grado que al representarla gráficamente en el plano cartesiano genera una línea recta.
Se puede denotar como:"푦=푓(푥)=푚푥+푏", donde “m” es la pendiente de la línea recta y “b” es por donde corta el eje “y”, ambas son constantes que pertenecen al conjunto de los números reales, es decir "푚,푏∈푅".
Las funciones lineales se pueden clasificar según los valores que toman la pendiente (m) y el corte en el eje “y” (b).
Cuando "푚=0" , se llama función constante de la forma "푦=푓(푥)=푏" y al representarla en el plano cartesiano se obtiene una línea recta horizontal.
Cuando la "푚≠0" y "푏=0", corta por el origen, se llama de proporcionalidad. Cuando la de proporcionalidad tiene "푚=1", se llama idéntica.

15. Cuando la función lineal tiene "푚≠ 0" y "푏≠0", se llama afín y corta el eje “x” en un punto diferente al origen.
Para graficar una función lineal, se representa el corte en “y”, y se tabula.
Ejemplo: graficar la función lineal "푦=푓(푥)=2푥+1"
Se tabula hallando el valor numérico de la función, asignando valores a la variable independiente cercanos al eje “y”.
푦=푓(−2)=2(−2)+1=−4+1=−3 푦=푓(−1)=2(−1)+1=−2+1=−1 푦=푓(0)=2(0)+1=0+1=1 푦=푓(1)=2(1)+1=2+1=3 푦=푓(2)=2(2)+1=4+1=5
Se representa en el plano cartesiano.
푥 푦
−2
−3
−1
−1
0
1
1
3
2
5

16. FUNCIÓN CUADRÁTICA
Una función cuadrática es una función polinómica de segundo grado que al representarla gráficamente en el plano cartesiano genera una parábola. Estas funciones tienen la forma:
푦=푓(푥)=푎푥2+푏푥+푐,푎≠0 y 푎,푏 푦 푐∈푅
Los componentes de una parábola son:

17. Según los valores que tome “a” la parábola tiene un comportamiento específico. Cuando "푎>0" , el vértice queda debajo de la parábola y abre hacia arriba.

18. Cuando "푎<0", el vértice queda arriba de la parábola y abre hacia abajo.
Otra forma de expresar una función cuadrática es 푦=푓(푥)=4푝(푥−ℎ)2+푘
Donde (ℎ,푘) es el vértice que es el punto donde la parábola pasa de crecer a decrecer o viceversa y “p” es el foco que es un punto fuera de ella, que cumple con que cada punto de la parábola tiene la misma distancia a este que hasta una recta horizontal llamada directriz.

19. Para hallar las coordenadas del foco de una parábola, se encuentra el valor de “p” y se utiliza:
Foco=[(ℎ+푝),푘]
Para hallar las coordenadas de la directriz de una parábola, se utiliza:
Foco=[(ℎ−푝),푘]
GRÁFICA DE UNA FUNCIÓN CUADRÁTICA
Para graficar una función cuadrática se debe llevar a la forma: 푦=푓(푥)=4푝(푥−ℎ)2+푘
Utilizando los casos de factorización.
Ejemplo: Graficar "푦=푓(푥)=4푥2+8푥+12"
푦=푓(푥)=(4푥2+8푥)+12
Se agrupan los dos primeros términos.
( 82) 2=(4)2=16
Se divide el segundo término por “2” y se eleva al cuadrado.

20. 푦=푓(푥)=(4푥2+8푥+16)+12−16
Se suma esta cantidad dentro del paréntesis y se resta afuera.
푦=푓(푥)=4(푥2+2푥+4)−4
En este caso se saca factor común al paréntesis.
푦=푓(푥)=4(푥+2)2−4
Se resuelve el trinomio cuadrado perfecto
Se define el vértice, el foco y la directriz.
Vértice
Foco
Directriz
푉=(ℎ,푘) 푉=(−2,−4)
4푝=4 푓표푐표= 44=1 푓표푐표=(ℎ+푝,푘) 푓표푐표=(−2+1,−4) 푓표푐표=(−1,−4)
퐷=(ℎ+푝,푘) 퐷=(−2−1,−4) 퐷=(−3,−4)
Se buscan los cortes en los ejes.
Cortes en el eje “x” 푦=0
0=4(푥+2)2−4
Se iguala a cero.
4(푥+2)2=4
Se despeja el “4”.
(푥+2)2= 44
Se pasa a a dividir el “4”.
(푥+2)2=1
Se divide.

21. 푥+2=±√1
Se elimina la potencia.
푥+2=±1
Se halla la raíz.
푥=−2±1
Se despeja “2”.
푥1=−2+1=−1
Tiene dos cortes se halla “푥1”.
푥2=−2−1=−3
Se halla “푥2”.
Corte en el eje “y” 푥=0
푦=푓(0)=4(0+2)2−4
Se reemplaza “푥” por “0.
푦=푓(0)=4(2)2−4
Se resuelve lo del paréntesis.
푦=푓(0)=4(4)−4
Se resuelve la potencia.
푦=푓(0)=16−4
Se resuelve la multiplicación
푦=푓(0)=12
Se resuelve la resta.
Se asignan valores a la variable independiente de la función cercanos al vértice y se tabula.
푓(−4)=4(−4+2)2−4=4(−2)2−4=4(4)−4=16−4=12 푓(−3)=4(−3+2)2−4=4(−1)2−4=4(1)−4=4−4=0 푓(−2)=4(−2+2)2−4=4(0)2−4=4(0)−4=0−4=−4 푓(−1)=4(−1+2)2−4=4(1)2−4=4(1)−4=4−4=0 푓(0)=4(0+2)2−4=4(2)2−4=4(4)−4=16−4=12

22. Se tabula y luego se grafica el vértice, el foco, la directriz, los cortes en los ejes y la tabulación.
푥 푦
−4
12
−3
0
−2
−4
−1
0
0
12

23. FUNCIÓN CÚBICA
Es una función polinómica de tercer grado de la forma:
푦=푓(푥)=푎푥3+푏푥2+푐푥+푑,푎≠0 y 푎,푏,푐 푦 푑 ∈푅
Para graficarlos se hallan los cortes y los máximos y mínimos de la función, el máximo es el vértice más alto y el mínimo es el vértice más bajo.
Ejemplo: graficar la siguiente función cúbica. 푦=푓(푥)=3푥3+2푥2−7푥+2,푎≠0
Se hallan los cortes, cortes en el eje “x”, cuando “푦=0.” 3푥3+2푥2−7푥+2=0
Se soluciona por factorización utilizando los casos de factorización. 3푥3+2푥2−7푥+2=(푥−1)(푥+2)(3푥+1)
Se hallan las raíces.
푥−1=0 푥=1
푥+2=0 푥=−2
3푥+1=0 푥=− 13
Se hallan los cortes en “푦 “cuando “푥=0”. 푦=푓(0)=3(0)3+2(0)2−7(0)+2

24. 푦=푓(0)=2
Se encuentran los máximos y mínimos utilizando la siguiente formula. 푥= −푏±√푏2−3푎푐 3푎 = −2±√(2)2−3(3)(−7) 3(3) 푥= −2±√4+639= −2±√679= −2±8.189 푥1= −2+8.189=0.69 푥2= −2−8.189=−1.13
Se reemplazan los valores obtenidos en la función. 푦=푓(0.69)=3(0.69)3+2(0.69)2−7(0.69)+2=−0.9 푦=푓(−1.13)=3(−1.13)3+2(−1.13)2−7(−1.13)+2=8.1
Los vértices son:
푉1=(0.69,−0.89) 푉2=(−1.13,8.13)
Se grafica la función teniendo en cuenta los datos obtenidos.

26. FUNCIÓN LOGARÍTMICA
Una función logarítmica es una función que tiene la forma:
y=f(푥)=log푎푥, Siendo 푎>0 y 푎≠1
Los logaritmos cumplen con las siguientes propiedades. y=log푎푥→a푦=푥
Teniendo en cuenta esta propiedad se puede deducir que no existe:
log−푎푥
log푎(−푥)
y=log푎0
También se deben tener en cuenta las siguientes propiedades.
log푎1=0
log푎푎=1
y=log푎푎푛=푛
Cuando “a” no aparece se dice que la base del logaritmo es “10”. log10푥=log푥
Cuando“푎=푒” se le llama logaritmo natural y se expresa: log푒푥=ln푥
Otras propiedades de los logaritmos son:

27. Logaritmo de un producto.
log푎(푥.푦)=log푎푥+log푎푦
Logaritmo de un cociente.
log푎( 푥 푦 )=log푎푥−log푎푦
Logaritmo de una potencia.
log푎푥푦=푦log푎푥
Logaritmo de una raíz.
log푎√푥 푦 = 1 푦 log푎푥
Cambio de base.
log푎푥= log푏푥 log푏푎
Para graficar una función logarítmica se utiliza la propiedad de cambio de base, se tabula con la ayuda de la calculadora y se representa en el plano cartesiano.
Ejemplo: graficar 푦=푓(푥)=log5푥
Se aplica el cambio de base para poder tabular con la calculadora. log5푥= log푥 log푎
Se tabula y se representa gráficamente en el plano cartesiano. 푥
14
12
1
2
3 푦
−0.86
−0.43
0
0.43
0.68

28. FUNCIÓN EXPONENCIAL
Una función exponencial tiene la forma: 푦=푓(푥)=퐾푎푥
Donde “k” y “a” son constantes que pertenecen al conjunto de los números reales, y “푎<0”y “푎≠1”.
Para graficar una función exponencial, se tabula alrededor del eje “y”.
Ejemplo: graficar la función exponencial 푦=푓(푥)=2푥.
푥
−2
−1
0
1
2 푦
0.25
0.5
1
2
4

29. FUNCIONES RACIONALES
Una función es irracional si tiene la forma:
푦=푓(푥)= 푃(푥) 푄(푥) , Donde 푄(푥)≠0
Para realizar la gráfica de una función racional se debe tener en cuenta.
● Si "푃(푥)" y "푄(푥)" tienen factores en común, es un hueco.
● Si "푃(푥)" y "푄(푥)" no tienen factores en común, es una asíntota vertical.
Una asíntota es una línea recta que se aproxima a una función haciéndose cada vez más pequeña la distancia entre ellas sin llegar a ser cero.
Las asíntotas se clasifican en:

30. ASÍNTOTA VERTICAL: son los ceros del polinomio del denominador que no se simplifican con el numerador.
ASÍNTOTA HORIZONTAL: estas dependen del grado de los polinomios.
Sea"푃(푥)" de grado "푛", y "푄(푥)" de grado "푚", entonces.
● Si "푚=푛" la asíntota horizontal son los coeficientes de los términos de mayor grado de los polinomios.
● si "푚>푛"la asíntota es el eje "푥", es decir, "푦=0"
● si "푚<푛"no tiene asíntota horizontal.
ASÍNTOTA OBLICUA: son cuando el numerador tiene un grado mayor al denominador, y es el cociente de la división.
En algunas funciones las asíntotas horizontales u oblicuas pueden ser cortadas en uno o varios puntos.
Ejemplo: graficar la función: 푦=푓(푥)= 4푥+13푥−2
Se hallan los cortes en el eje "푦", es decir cuando "푥=0". 푦=푓(0)= 4(0)+13(0)−2= 0+10−2=− 12

31. El corte en el eje "푦" es en "(0,− 12)".
Se hallan los cortes en el eje "푥", es decir cuando "푦=0". 4푥+13푥−2=0 4푥+1=0 4푥=−1 푥=− 14
El corte en el eje "푦" es en "(− 14,0)".
Se hallan las asíntotas verticales. 3푥−2=0 3푥=2 푥= 23
Se hallan las asíntotas horizontales, como los grados de los polinomios son los iguales son los coeficientes. 푦= 43
Como tiene asíntota horizontal no tiene asíntota oblicua.
Se tabula alrededor de la asíntota horizontal y se hace la gráfica en un plano cartesiano.

32. Ejemplo: graficar la función: 푦=푓(푥)= 푥3 푥2+3푥−10
Se hallan los cortes en el eje "푦", es decir cuando "푥=0". 푦=푓(0)= (0)3(0)2+3(0)−10= 0−10=0
El corte en el eje "푦" es en "(0,0)".
Se hallan los cortes en el eje "푥", es decir cuando "푦=0".
푥3 푥2+3푥−10=0 푥3=0 푥=0

33. El corte en el eje "푦" es en "(0,0)".
Se hallan las asíntotas verticales.
푥2+3푥−10=0 (푥+5)(푥−2)=0
푥+5=0 푥=−5
푥−2=0 푥=2
No tiene asíntotas horizontales ya que el grado del polinomio de arriba es mayor que el de abajo, por lo tanto tiene asíntota oblicua.
Se ordenan los polinomios.
La asíntota oblicua es el cociente entre los polinomios, en este caso es “푦=푥−3"

34. Se tabula alrededor de las asíntotas verticales y se grafica en un plano cartesiano.

35. FUNCIÓN VALOR ABSOLUTO
Es una función que está definida por: 푓(푥)=|푥|={ −푥,푥<0 푥,푥≥0
Para graficar una función valor absoluto se tabula y se representa en el plano cartesiano.
Ejemplo: graficar "푓(푥)=|푥+5|”
Se representa en la definición de valor absoluto. 푓(푥)=|푥+5|={ −푥−5,푥<−5 푥+5,푥≥−5
푥
−6
−7
−8
−9
−10 푦= 푓(푥)=−푥−5
1
2
3
4
5
푥
−5
−4
−3
−2
−1 푦= 푓(푥)=푥+5
0
1
2
3
4
Y se representa gráficamente.

36. FUNCIÓN PARTE ENTERA
Es una función que cumple con:
푓(푥)=⟦푥⟧=푛 Para todo 푛∈푍, cumple con 푛≤푥<푛+1
Es escoger el menor entero del intervalo dado.
Ejemplo: graficar “ 푓(푥)=⟦푥⟧”. 푛≤푥<푛+1
푥
푛
푓(푥)=푛
−3
[−3,−2)
−3
−2
[−2,−1)
−2
−1
[−1,0)
−1
0
[0,1)
0

37. 1
[1,2)
1
2
[2,3)
2
Ejemplo: graficar “ 푓(푥)=⟦ 푥 2 ⟧+푥”.
푛≤ 푥 2<푛+1 2푛≤푥<2푛+2
푥
푛
푓(푥)=푛+푥
−3
[−6,−4)
푦=−3+푥
−2
[−4,−2)
푦=−2+푥
−1
[−2,0)
푦=−1+푥
0
[0,2)
푦=푥
1
[2,4)
푦=1+푥
2
[4,6)
푦=2+푥

38. FUNCIÓN A TROZOS
Es una función formada por dos o más funciones que están definidas en intervalos separados, su forma es: 푓(푥)={ 푃(푥),푎≤푥<푏 푄(푥),푏≤푥<푐
Para graficar se hace función por función respetando los intervalos definidos.
Ejemplo: graficar: 푓(푥)={ 푥+4,푥<−2 ⟦푥⟧,−2≤푥<2 푥2−8,2≤푥
Se tabula cada función en su intervalo correspondiente.
푓(푥)=푥+4
푓(푥)=⟦푥⟧
푓(푥)=푥2−8
푥
푦
푥
푓(푥)=푛
푥
푦
−5
−1
[−2,−1)
푦=−2
2
−4
−4
0
[−1,0)
푦=−1
3
1
−3
1
[0,1)
푦=0
4
8
−2
2
[1,2)
푦=1
5
17
y se representa en el plano cartesiano.

40. OPERACIONES CON FUNCIONES
Las operaciones con funciones se hacen de la misma manera que las operaciones con polinomios. Las propiedades de las operaciones con funciones son:
Sean “ 푓(푥)” y “ 푔(푥)” dos funciones:
(푓+푔)(푥)= 푓(푥)+푔(푥)
Suma de funciones
(푓−푔)(푥)= 푓(푥)−푔(푥)
Resta de funciones
(푓.푔)(푥)= 푓(푥).푔(푥)
Multiplicación de funciones
( 푓 푔 )(푥)= 푓(푥) 푔(푥)
División de funciones
(푓표푔)(푥)= 푓(푔(푥))
Función compuesta
Ejemplos: sean 푓(푥)=푥+1 y 푔(푥)=푥2−5푥−6 realizar:
(푓+푔)(푥)= 푓(푥)+푔(푥)
(푥+1)+(푥2−5푥−6) 푥2−4푥−5
(푓−푔)(푥)= 푓(푥)−푔(푥)
(푥+1)−(푥2−5푥−6) −푥2+6푥+7
(푓.푔)(푥)= 푓(푥).푔(푥)
(푥+1).(푥2−5푥−6) 푥3−4푥2−11푥−6
( 푓 푔 )(푥)= 푓(푥) 푔(푥)
푥+1 푥2−5푥−6= 푥+1(푥−6)(푥+1) = 1 푥−6=
(푓표푔)(푥)= 푓(푔(푥))
푓(푥2−5푥−6) =(푥2−5푥−6)+1 =푥2−5푥−5

41. FUNCIÓN INVERSA
Una función tiene inversa si es “1” a “1” es decir, es inyectiva, se define como:
“푓−1(푦)=푥” , si y solo si “ 푓(푥)=푦”
Para hallar una función inversa se tiene en cuenta lo siguiente:
Ejemplo: hallar la función inversa de 푦=푓(푥)=3푥+2
Primero se compruebas si la función es “1” a “1”.

42. Se escribe la función de la forma “ 푦=푓(푥) “y se despeja “x”. 푦=3푥+2→푦−2=3푥→ 푦−23=푥
Se intercambian las variables y se obtiene la función inversa y se grafica, 푥−23=푦

43. Ejemplo:
Hallar la función inversa de 푦=푓(푥)=푥2 para los 푥∈푅.
Se comprueba si la función es inyectiva.
Cuando la función no es inyectiva se puede restringir el dominio para que lo sea, la función sería 푦=푓(푥)=푥2 para los 푥∈푅+.
Se escribe la función de la forma “ 푦=푓(푥) “y se despeja “x”. 푦=푥2 √푦=푥
Se intercambian las variables y se obtiene la función inversa. √푥=푦
Y se grafican.

45. BIBLIOGRAFÍA  Richard Stallman. Enciclopedia universal. 1999. disponible en: www.wikipedia.com  Juan Carlos Fernández Gordillo. Matemáticas. Valencia España. Edifesa, Disponible en: www.vitutor.com  Chad Harley. Steve Chen. Jawed Karim. Reproductor de video online. 15 de febrero de 2005. Disponible en http://www.youtube.com
 Vladimir Moreno Gutierrez. Mauricio Restrepo López. Delta 8. Ed Norma. 2008
 William Hernando Dueñas.Luz Dary García Forero.Alix Aleida Garavito Ramírez. Con lógica 8. Ed Educar. 2012.
 William Hernando Dueñas.Luz Dary García Forero.Alix Aleida Garavito Ramírez. Con lógica 9. Ed Educar. 2012.
 Vladimir Moreno Gutiérrez. Mauricio Restrepo López. Delta 9. Ed Norma. 2008.
 Aurelio Baldor. Álgebra de Baldor. Publicaciones cultural Mexico.1997
 Vladimir Moreno Gutiérrez. Mauricio Restrepo López. Delta 10. Ed Norma. 2008.
 Vladimir Moreno Gutiérrez. Mauricio Restrepo López. Delta 11. Ed Norma. 2008.
 William Hernando Dueñas. Luz Dary García Forero. Alix Aleida Garavito Ramírez. Con lógica 10. Ed Educar. 2012.
 William Hernando Dueñas. Luz Dary García Forero. Alix Aleida Garavito Ramírez. Con lógica 11. Ed Educar. 2012.

46. SOFTWARE  Kvisoft Inc. FlipBook Maker Pro. 2014. Disponible en: www.kvisoft.com/flipbook-maker-pro  Diego Uscanga. aTube Catcher.2011. Disponible en: www.atubecatcher.es
VIDEOS
 Eusebio Molina Rodríguez. Concepto de función. Parte 1. 2012. Disponible en: https://www.youtube.com/watch?v=6A2Lf5cbS-s
 Marcos Antonio Fatela. Funciones inyectivas, suryectivas y biyectivas. 2013. Disponible en: https://www.youtube.com/watch?v=hZeIR6paRLM
 Anneliesse Sánchez. Funciones par e impar. 2011. Disponible en: https://www.youtube.com/watch?v=FqZPRJQPdJQ
 Abel Esteban Ortega Luna. Función creciente, decreciente y constante.2014. Disponible en: https://www.youtube.com/watch?v=rKjPXCGgyOQ
 Abel Esteban Ortega Luna. Tabulación y gráfica de una función lineal.2014. Disponible en: https://www.youtube.com/watch?v=K-C6l6tH95Q
 Julio Alberto Ríos Gallego. Análisis de una función cuadrática. 2011. Disponible en: https://www.youtube.com/watch?v=0pUnHF1FJ2s
 Jampier López. Función cúbica. 2010. Disponible en : https://www.youtube.com/watch?v=Bhm1N26YolA

47.  Hugo Rolando Tejada García. Funciones logarítmicas- parte 1. 2009. Disponible en: https://www.youtube.com/watch?v=MMXOEhzSsYY
 María Justina Ruibal Zatyczyc. Función exponencial explicación. 2011. Disponible en: https://www.youtube.com/watch?v=aN0aEs_efy0
 Cesar Echevarría. Grafica de una función racional. 2010. Disponible en: https://www.youtube.com/watch?v=HGdiXiVxMxA
 Carlos W Apaza Huacho. Función valor absoluto. 2011. Disponible en: https://www.youtube.com/watch?v=3koeLKRJlBk
 Natalia carrasco. Función valor absoluto y parte entera. 2012. Disponible en: https://www.youtube.com/watch?v=08b_JcSE6M0
 Julio Alberto Ríos Gallego. Gráfica, dominio y rango de una función a trozos. 2011. Disponible en: https://www.youtube.com/watch?v=AU1GVkYD78w
 Matemática tuya. Operaciones con funciones. 2012. Disponible en: https://www.youtube.com/watch?v=orDntRpxuvs
 Julio Alberto Ríos Gallego. Hallar la inversa de una función. 2011. Disponible en: https://www.youtube.com/watch?v=TxRpKrQJsdw