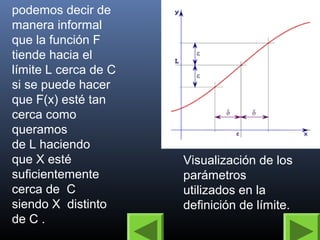
Este documento describe la historia y definición formal del concepto matemático de límite. Explica que los antiguos griegos utilizaban conceptos basados en límites para calcular áreas. Más tarde, en los siglos XVII y XIX, matemáticos como John Wallis, Louis Cauchy y Karl Weierstrass formularon definiciones más precisas del límite, culminando con la definición formal de Weierstrass usando épsilon y delta. Los límites son fundamentales en análisis matemático para definir conceptos como convergencia, contin

1. Evaluacion integradora de analisis matematico
Gabriel Lezcano
Javier Puzio
Emanuel Rakosky
Agustín Benitez

2. Limites Matemáticos
Los antiguos griegos utilizaban procedimientos
basados en límites para calcular áreas, como el
área del círculo.

3. John Wallis (1616-1703) es quien
formulo la primera definición de
limite en el siglo XVII.
En el año 1821 Louis Cauchy, en su
obra Cauchy da una nueva
definición del limite
John Wallis

4. Treinta años mas tarde el alemán Karl Weierstrass
realizaría le definición formal del limite utilizando el
épsilon y delta
Karl Weierstrass

5. Definición formal de limite:
“El límite de una función , cuando x tiende a c
es L si y sólo si para todo épsilon existe un
delta tal que para todo número real x en el
dominio de la función si cero es menor que el
valor absoluto de x-c y este es menor al delta
entonces el valor absoluto de f(x)-L es menor
a épsilon.”

6. podemos decir de
manera informal
que la función F
tiende hacia el
límite L cerca de C
si se puede hacer
que F(x) esté tan
cerca como
queramos
de L haciendo
que X esté
suficientemente
cerca de C
siendo X distinto
de C .
Visualización de los
parámetros
utilizados en la
definición de límite.

7. LIMITES
El limite describe la tendencia de una funcion , a medida que
los parametros de esa funcion se acercan a determinado
valor.
En analisis matematico este concepto se usa para definir los
conceptos fundamentales de convergencia , cntinuidad ,
derivacion , integracion , entre otros…
Los limites son importantes porque nos ayudan a resolver
eficazmente los problemas que nos presentan en un ejercicio
de un tema determinado. Cada limite no puede dar una
solucion diferente , por ejemplo en un ejercicio que
resolvamos podemos conseguir que podria ser una funcion
indeterminada , la cual es cuando el resultado obtenido es
0/0.
Con lo cual tambien podremos encontrar funciones que si
tengan soluciones o funciones determinadas , es decir , nos
ayuda a encontrarle alguna solucion posible a una funcion

9. Solución:
Lim f(x)= 2
X-0
Lim f(x)= -3
X-2
Lim f(x)= Error
X-8

10. Uso de los limites en la vida cotidiana
un ejemplo de como utilizar los limites en la
adminstración
es como se elaboran gráficas para saber el nivel
de producción y para encontrar el menor costo
posible esto para generar una mayor ganancia
para la misma empresa
un ejemplo de esto es cuando presenta una alza
en los costos de la materia prima esto
eventualmente generara un cambio en cuanto el
costo que esta genero anterior mente

11. Aplicación en las ciencias
En el calculo análisis real y matemático este
concepto se utiliza para definir los conceptos
fundamentales de convergencia, continuidad,
derivación, integración, entre otros

12. Si una sucesión tiene límite, se dice
que es una sucesión convergente, y
que la sucesión converge o tiende al
límite.
Ejemplo:
La sucesión 1/1, 1/2, 1/3, 1/4,
... converge al límite 0

13. Derivada
Un ejemplo habitual aparece al estudiar
el movimiento: si una función representa
la posición de un objeto con respecto al
tiempo, su derivada es la velocidad de
dicho objeto.