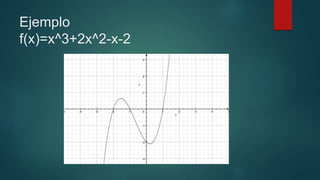
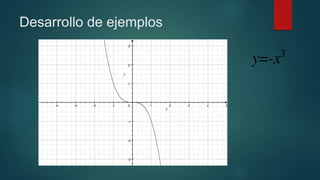
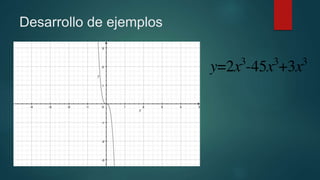
Este documento resume la historia y definición de las ecuaciones de tercer grado. Explica que el matemático persa Omar Jayyam generalizó los métodos para calcular raíces cúbicas y de grado superior en el siglo XII, aunque no se pudo demostrar que no se pueden hallar las raíces de ecuaciones de tercer grado mediante regla y compás hasta 750 años después. Define una ecuación de tercer grado como una función cuyo mayor exponente es tres, y ofrece un ejemplo de una función cúbica. Final

1. Ecuaciones de tercer
grado
JUAN SEBASTIÁN DIAZ GIRALDO
JACOBO OSPINA RENDÓN
JUAN ESTEBAN TOBÓN SARMIENTO

2. Historia
 En el siglo XII, el matemático persa Omar Jayyam generalizó los métodos indios
de extracción de raíces cuadradas y cúbicas para calcular raíces cuartas, quintas
y de grado superior. En su Tesis sobre demostraciones de álgebra y comparación
desarrolla el primer procedimiento de solución de las ecuaciones cuadráticas y
cúbicas a partir de las secciones cónicas, que permite encontrarles una raíz
positiva y asimismo logra demostrar que tienen al menos una segunda raíz. Su
afirmación de que no se pueden hallar las raíces de las ecuaciones de tercer
grado mediante regla y compás no pudo ser demostrada hasta 750 años más
tarde. Y la teoría de las ecuaciones de tercer grado no fue desarrollada hasta el
siglo XVII, por René Descartes.
En 1070 escribió su famoso trabajo de álgebra Tratado sobre demostraciones de
problemas de álgebra, que contiene una completa clasificación de ecuaciones
cúbicas resueltas geométricamente, mediante la intersección de secciones
cónicas. Y es que intentó clasificar ecuaciones cuadráticas con éxito, aunque no
pudo encontrar la solución para todas las ecuaciones cúbicas, a pesar de estar
seguro de que era posible hacerlo, ya que en algunos casos halló soluciones
geométricas

3. Definición
 Es una función cuyo mayor exponente es tres, se le denomina funciones
cubicas, también la forma:
Siendo a, b, c, d números reales y diferentes a cero (0).
 El rango y el dominio de las funciones polinómicas de tercer grado son
todos los números reales.
 Puede existir máximo tres intersecciones y mínimo una en el eje “y”.

4. Ejemplo
f(x)=x^3+2x^2-x-2

5. Aplicaciones
Las funciones polinómicas tienen una gran utilización en la elaboración de
modelos que describen fenómenos reales. Algunos de ellos son:
 La concentración de una sustancia en un compuesto.
 La distancia recorrida por un móvil a velocidad constante.
 Compra-venta de cierta cantidad de objetos a un precio unitario.
 Salario de trabajadores más su comisión.
 Variación de la altura de un proyectil.

6. Desarrollo de ejemplos

7. Desarrollo de ejemplos

8. Gracias 