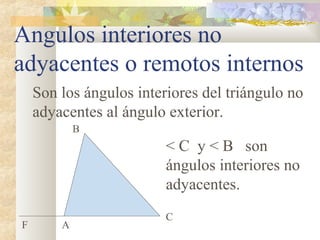
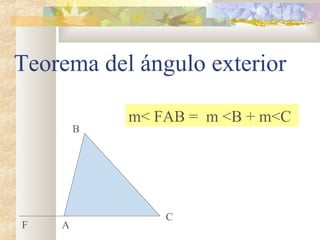
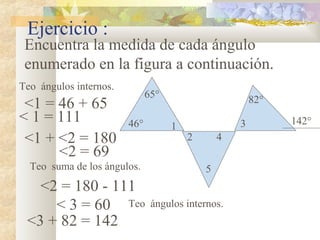
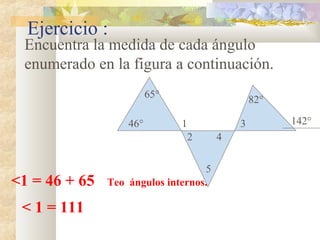
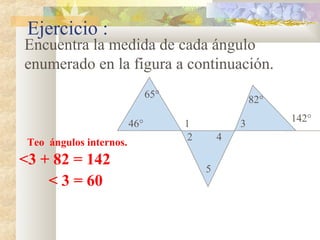
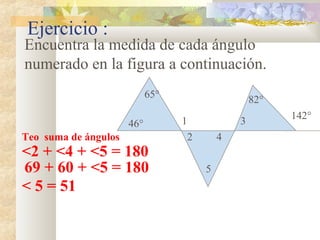
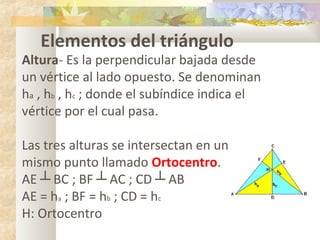
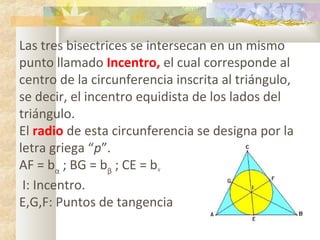
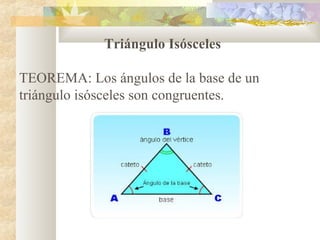
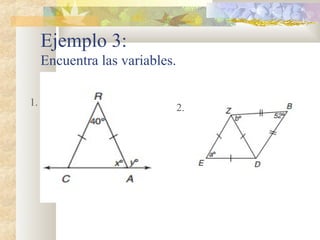
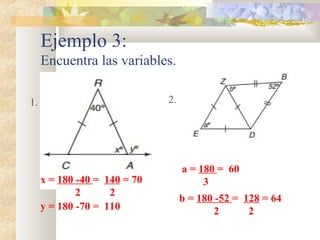
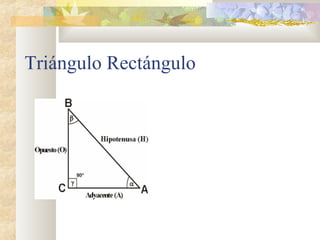
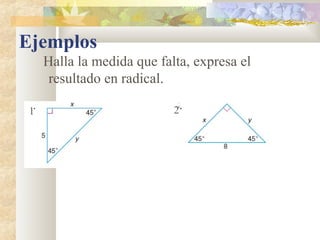
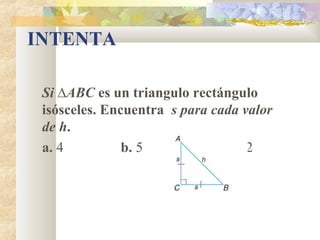
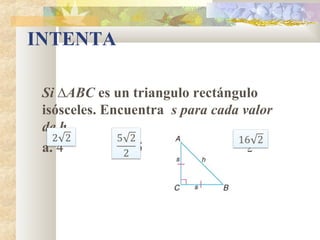
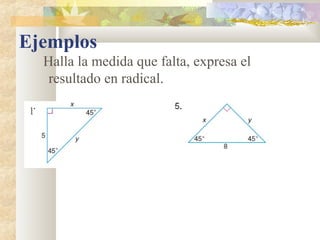
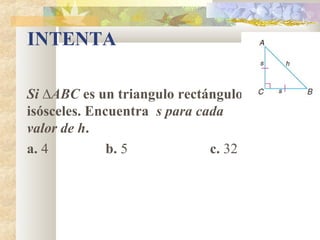
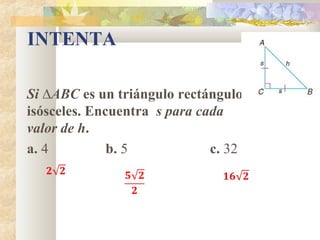
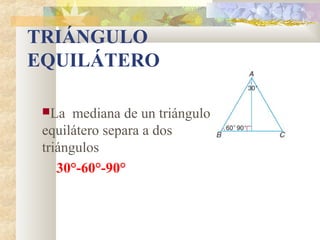
1) El documento presenta información sobre teoremas y conceptos geométricos relacionados con triángulos, incluyendo la suma de los ángulos internos, ángulos exteriores, bisectrices, alturas y medianas. 2) Se explican y ejemplifican el Teorema de Pitágoras y sus aplicaciones a triángulos rectángulos e isósceles. 3) Se define el triángulo equilátero y se establece que sus ángulos internos miden 60° cada uno.

1. Unidad 9.1 Paralelas y Perpendiculares
Teoremas y Postulados de triángulos
Prof. Carmen Batiz
UGHS

2. 1. Dibuja un triángulo CFG.
C
F
G

3. 2. Enumera los vértices.
C
F
G
1
2 3

4. 3. Recorta éstos.
C
F
G
1
2 3

5. 4. Une los tres ángulos y
explica que ocurrió.
1
2
3

6. Generalización
1
2
3
Teorema de la suma de los ángulos en
un triángulo
La suma de los ángulos
internos de un triángulo
es 180°.

7. Ejemplo 1
Halla el valor de x en los siguientes triángulos.
3x + x +30 + 90 = 180
4x + 120 = 180
4x = 60
x = 15°
2x + x – 10 = 110
3x=120
x = 40 °

8. Angulo Exterior
< BAF es un ángulo exterior
del ABC
A
B
C
F
Es formado por un lado del triángulo y
la prolongación de otro de sus lados.
¿Cuántos ángulos
exteriores tendrá un
triángulo?

9. Angulos interiores no
adyacentes o remotos internos
< C y < B son
ángulos interiores no
adyacentes.
A
B
C
F
Son los ángulos interiores del triángulo no
adyacentes al ángulo exterior.

10. Teorema del ángulo exterior
La medida de un ángulo exterior de un
triángulo es igual a la suma de las
medidas de los ángulos internos o
interiores no adyacentes.

11. Teorema del ángulo exterior
m< FAB = m <B + m<C
A
B
C
F

12. Ejercicio :
Encuentra la medida de cada ángulo
enumerado en la figura a continuación.
<2 = 69
Teo ángulos internos.
<1 + <2 = 180
< 1 = 111
<1 = 46 + 65
<2 = 180 - 111
< 3 = 60
<3 + 82 = 142
65°
46° 1
2
5
4
3
82°
142°
Teo ángulos internos.
Teo suma de los ángulos.

13. Ejercicio :
Encuentra la medida de cada ángulo
enumerado en la figura a continuación.
65°
46° 1
2
5
4
3
82°
142°

14. Ejercicio :
Encuentra la medida de cada ángulo
enumerado en la figura a continuación.
65°
46° 1
2
5
4
3
82°
142°
Teo ángulos internos.
< 1 = 111
<1 = 46 + 65

15. Ejercicio :
Encuentra la medida de cada ángulo
enumerado en la figura a continuación.
<2 = 69
<1 + <2 = 180
65°
46° 1
2
5
4
3
82°
142°
Def. Par lineal
<2 = 180 - 111

16. Ejercicio :
Encuentra la medida de cada ángulo
enumerado en la figura a continuación.
Teo ángulos internos.
< 3 = 60
<3 + 82 = 142
65°
46° 1
2
5
4
3
82°
142°

17. Ejercicio :
Encuentra la medida de cada ángulo
numerado en la figura a continuación.
< 5 = 51
<2 + <4 + <5 = 180
69 + 60 + <5 = 180
65°
46° 1
2
5
4
3
82°
142°
Teo suma de ángulos

18. TAREA
Geometry Concepts and Applications
Glencoe p. 26, 39

19. Elementos del triángulo
Altura- Es la perpendicular bajada desde
un vértice al lado opuesto. Se denominan
ha , hb , hc ; donde el subíndice indica el
vértice por el cual pasa.
Las tres alturas se intersectan en un
mismo punto llamado Ortocentro.
AE ┴ BC ; BF ┴ AC ; CD ┴ AB
AE = ha ; BF = hb ; CD = hc
H: Ortocentro

20. Bisectriz- Es la recta que pasa por un vértice y
divide al ángulo en dos ángulos congruentes. Se
denominan bα
, bβ
y bᵞ
; donde el subíndice indica
el ángulo que dimidia.

21. Las tres bisectrices se intersecan en un mismo
punto llamado Incentro, el cual corresponde al
centro de la circunferencia inscrita al triángulo,
se decir, el incentro equidista de los lados del
triángulo.
El radio de esta circunferencia se designa por la
letra griega “p”.
AF = bα
; BG = bβ
; CE = bᵞ
I: Incentro.
E,G,F: Puntos de tangencia

22. Mediana- Es el segmento de recta que une los
puntos medios de dos lados del triángulo.
•P,Q, R : Puntos medios (medianas) de los lados
PQ, QR, RP
Baricentro –punto donde se unen las medianas

23. TEOREMA:
El segmento que une los puntos medios de
dos lados de un triángulo es paralelo al
tercer lado y su longitud es la mitad de ese
lado.
Si QP y QR son medianas del ∆ ABC
entonces PR || AB y PR = ½ AB

24. Ejemplo 1:
1. Nombra una altura.
2. Nombra un segmento que sea una bisectriz perpendicular.
3. Nombra un segmento que no es altura ni bisectriz
perpendicular.

25. Ejemplo 1:
1. Nombra una altura.
2. Nombra un segmento que sea una bisectriz perpendicular.
3. Nombra un segmento que no es altura ni bisectriz
perpendicular.
FD
FD
AG

26. EJEMPLO 2
Si en el ∆ACD, DB bisecta <ADC, y CE bisecta
<ACD.
1. ¿Cuál es la medida de <3, si m<ACD = 36?
2. ¿Cuál es la medida de <ADB, si m<BDC =39?

27. EJEMPLO 2
Si en el ∆ACD, DB bisecta <ADC, y CE bisecta
<ACD.
1. ¿Cuál es la medida de <3, si m<ACD = 36?
2. ¿Cuál es la medida de <ADB, si m<BDC =39?
36/2 = 18
39 x 2 = 78

28. TAREA
Geometry Concepts and Applications
Glencoe p. 31,32,33

29. Triángulo Isósceles
TEOREMA: Los ángulos de la base de un
triángulo isósceles son congruentes.

30. Ejemplo 3:
Encuentra las variables.
1.
2.

31. Ejemplo 3:
Encuentra las variables.
1. 2.
y = 180 -70 = 110
x = 180 -40 = 140 = 70
2 2
a = 180 = 60
3
b = 180 -52 = 128 = 64
2 2

32. Ejemplo 4:
En ∆ADF, si AD = x+6 y DF =3x – 10. ¿Cuál es la
medida de AD?

33. Ejemplo 4:
En ∆ADF, si AD = x+6 y DF =3x – 10. ¿Cuál es la
medida de AD?
x+6 = 3x -10 Teo. Triángulo isósceles
6 +10 = 3x – x
16 = 2x
x = 8
AD = x + 6
AD = 8 + 6
AD = 14

34. TAREA
Geometry Concepts and Applications
Glencoe p. 34

35. Triángulo Rectángulo

36. Actividad:
MATERIALES:
1.Papel cuadriculado
2.Tijeras
PROCEDIMIENTO:
1.Recorta dos cuadrado de diferentes tamaños.
Algunas unidades que puedes utilizar son: 3, 4, ó 6 y
8 y sus múltiplos.
2.Une los dos cuadrados formando entre ellos un
triángulo rectángulo como se demuestra a
continuación:

37. Actividad:

38. Actividad:
3. Ahora, encuentra un cuadrado que pueda acomodarse en
el tercer lado del triángulo formado.
4. Contesta las siguientes preguntas:
a. ¿Cuál es el triángulo formado por los cuadrados?
b. Identifica los lados del triángulo.
c. Determina la medida de los lados de los cuadrados y
luego el área de cada una de ellos.
d. ¿Puedes hacer alguna conclusión?
5. Veamos las conclusiones de los diferentes grupos para
generalizar…

39. TEOREMA DE PITÁGORAS
Establece que en todo
triángulo rectángulo,
el cuadrado de la
longitud de la
hipotenusa es igual a la
suma de los cuadrados
de las respectivas
longitudes de los
catetos.

40. Triángulos pitagóricos
Una triángulo pitagórico consiste en una tupla de tres
enteros positivos a, b, c que cumplen que a² + b² = c².
( 3 , 4 , 5 ) ( 5, 12, 13) ( 7, 24, 25) ( 8, 15, 17)
( 9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85)
(16, 63, 65) (20, 21, 29) (28, 45, 53) (33, 56, 65)
(36, 77, 85) (39, 80, 89) (48, 55, 73) (65, 72, 97)

41. EJEMPLO 5
Halla la medida del lado que en los siguientes triángulos
rectángulos. Puedes expresar el resultado en radical simple.
1. 2.

42. EJEMPLO 5
Halla la medida del lado que en los siguientes triángulos
rectángulos. Puedes expresar el resultado en radical simple.
1. 2.
a2
+ b2
= c2
32
+ 52
= c2
9+ 25 = c2
34 = c2
c = ≈ 5.8
a2
+ b2
= c2
a2
+ 252
= 292
a2
+ 625 = 841
a2
= 841-625
a = =

43. TAREA
Geometry Concepts and Applications
Glencoe p. 36

44. Actividad
MATERIALES: Papel cuadriculado y transportador
PASO 1: Dibuja un cuadrado cuyas dimensiones sea 4 unidades.
Etiqueta los vértices del cuadrado A, B, C, and D.
PASO 2: Dibuja una diagonal AC.
PASO 3: Utiliza el transportador para medir el <CAB y < ACB.
PASO 4: Utiliza el teorema de Pitágoras para hallar AC. Expresa el
resultado en la forma mas simple. (radical)
PASO 5: Repite el proceso para un cuadrado de 6 unidades y de 8
unidades.
PASO 6. Haz una conclusión relacionando los lados del cuadrado y
su diagonal.

45.  □ ABCD cuyos lados mide
____
 <CAB mide y < ACB mide
____
 AC = _____
A
B
C
Formato para los tres cuadrados, recuerda
concluir al final.
D
Actividad 1

46. CONCLUSIÓN:
 Al pasar una diagonal en los tres cuadrados, se formaron
triángulo______________ cuyos ángulos miden ______,
_______, ________. Puedo llegar a la conclusión que cada
triángulo es un triángulo ________________ y
___________________.
 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________
 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________
 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________

47. CONCLUSIÓN:
 Al pasar una diagonal en los tres cuadrados, se formaron
triángulo______________ cuyos ángulos miden ______,
_______, ________. Puedo llegar a la conclusión que cada
triángulo es un triángulo ________________ y
___________________.
isósceles
45∘ 45∘ 90∘
isósceles
rectángulo
4 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________
 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________
 El triángulo que mide _____ unidades y _____ unidades, su hipotenusa
mide:________
4
6 6
8 8

48. Actividad 2
MATERIALES: Libreta y transportador
PASO 1 Construye un triángulo equilátero cuyos lados
midan 2 unidades. Etiqueta los vértices A, B, y
C.
PASO 2 Encuentra el punto medio del lado AB y etiqueta
al punto como D. Traza el segmento CD, que es
la mediana .

49. Actividad 2
PASO 3 Utiliza el transportador para medir <ACD, < A, y < CDA.
PASO 4 Utilizaq la regla para medir AD.
PASO 5 Copia y completa la siguiente tabla Utiliza el teorema de
Pitágoras pa encontrar CD. Escribe la contestación en
radical más simple.

50. Actividad 2
PASO 3 Utiliza el transportador para medir <ACD, < A, y < CDA.
PASO 4 Utilizaq la regla para medir AD.
PASO 5 Copia y completa la siguiente tabla Utiliza el teorema de
Pitágoras pa encontrar CD. Escribe la contestación en
radical más simple.

51. TRIÁNGULO 45°-45°-90°
En un triángulo isósceles), la medida de la
hipotenusa es la medida del cateto
multiplicado por .

52. Ejemplos
Halla la medida que falta, expresa el
resultado en radical.
1 2

53. Ejemplos
Halla la medida que falta, expresa el
resultado en radical.
1 2
55

54. INTENTA
Si ∆ABC es un triangulo rectángulo
isósceles. Encuentra s para cada valor
de h.
a. 4 b. 5 c. 32

55. INTENTA
Si ∆ABC es un triangulo rectángulo
isósceles. Encuentra s para cada valor
de h.
a. 4 b. 5 c. 32

56. TRIÁNGULO EQUILÁTERO
 Un triángulo equilátero tiene tres lados iguales y
tres ángulos iguales.
 Si la medida de los ángulos de un triángulo es
180°, entonces la medida de cada ángulo en un
triángulo equilátero es de 60°.
 Si se dibuja una mediana desde el vértice A al lado
BC, entonces la mediana es la bisectriz del ángulo
A.
 La mediana es el segmento que une el punto
medio de un lado con el vértice opuesto.
 La bisectriz de un ángulo es el segmento que
divide al ángulo en dos ángulos que tienen la
misma medida.

57. TRIÁNGULO
EQUILÁTERO
La mediana de un triángulo
equilátero separa a dos
triángulos
30°-60°-90°

58. TRIÁNGULO 30°-60°-90°
En un triángulo 30°-60°-90° (triángulo
equilátero), la hipotenusa es el doble del
cateto menor y el otro cateto es el cateto
menor multiplicado por multiplicado por
.

59. Ejemplos:
Halla la medida que falta, expresa el
resultado en radical.
21 2 3

60. Ejemplo
Halla la medida que falta, expresa el
resultado en radical.
2
1 2 3

61. Ejemplos
Halla la medida que falta, expresa el
resultado en radical.
1

62. Ejemplos
Halla la medida que falta, expresa el
resultado en radical.
1 2
55

63. INTENTA
Si ∆ABC es un triangulo rectángulo
isósceles. Encuentra s para cada
valor de h.
a. 4 b. 5 c. 32

64. INTENTA
Si ∆ABC es un triángulo rectángulo
isósceles. Encuentra s para cada
valor de h.
a. 4 b. 5 c. 32

65. Actividad de cierre
En tu libreta de avalúo, en la parte de
Reflexiones completa la siguiente
aseveración:
Describe en tus propias palabras los
Triángulos 30°-60°-90° y 45°-45°-90°

66. Tarea :
 Geometry workbook p. 33,34