Descargar como PDF, PPTX
Subido porFrancisco Sandoval
4 problemas electrostatica_valor_en_frontera
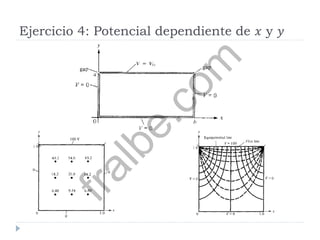
Este documento presenta los conceptos fundamentales de electrostática relacionados con problemas que involucran valores en la frontera. Explica las ecuaciones de Poisson y Laplace, el teorema de unicidad, y los procedimientos generales para resolver estas ecuaciones. También cubre temas como resistencia, capacitancia, y el método de imágenes, ilustrando estos conceptos con varios ejemplos.
Más contenido relacionado
Similar a 4 problemas electrostatica_valor_en_frontera
4 problemas electrostatica_valor_en_frontera
- 1. Problemas de electrostáticacon valor en la frontera Teoría de Campos Electromagnéticos Francisco A. Sandoval fralbe.com
- 2. Agenda Flashback Introducción Ecuaciones de Poisson y de Laplace Teorema de Unicidad Procedimiento general para resolver la ecuación de Poisson o de Laplace Resistencia y capacitancia Método de imágenes fralbe.com
- 3.
- 4.
- 5. Introducción Considerar problemasprácticos de electrostática, sólo se conocen condiciones electrostáticas (carga y potencial) en algunas fronteras y se desea hallar 𝑬 y 𝑉 en toda la región (problemas con valor en la frontera). Ecuación de Poisson o Laplace Método de imágenes Deducir resistencia y capacitancia Ecuación de Laplace. fralbe.com
- 6. Ecuaciones de Poissony de Laplace fralbe.com
- 7. Ecuaciones de Poissony Laplace Se deducen de ley de Gauss (caso medio material lineal) Y Para un medio no homogéneo En una región sin carga Ecuación de Poisson Ecuación de Laplace fralbe.com
- 8.
- 9.
- 10. Teorema de Unicidad Las diversas soluciones que es posible obtener de la ecuación de Laplace son diferentes entre sí? Si una solución de la ecuación de Laplace satisface un conjunto dado de condiciones en la frontera, ¿ Es la única solución posible? Si, solo hay una solución El teorema de unicidad se comprueba por contradicción. Se parte del supuesto de que dos soluciones 𝑉1 y 𝑉2 de la Ec. de Laplace satisfacen las condiciones en la frontera prescrita. Teorema de unicidad: Si se puede determinar que una solución de la ecuación de Laplace satisface las condiciones en la frontera, esa solución es la única. fralbe.com
- 11. Teorema de Unicidad Cosas que describen inequívocamente a un problema: La ecuación diferencial apropiada (para este caso, de Laplace o Poisson) La región de la solución Las condiciones en la frontera fralbe.com
- 12. Procedimiento general para resolverla ecuación de Poisson fralbe.com
- 13. Procedimiento general pararesolver la ecuación de Poisson 1. Se resuelve la ec. de Laplace (si 𝜌 𝑣 = 0) o la de Poisson (si 𝜌 𝑣 ≠ 0) mediante: 1. Integración directa cuando 𝑉 es una función de una variable. 2. Separación de variables cuando 𝑉 es una función de más de una variable. 2. Se aplican las condiciones en la frontera para determinar la solución única de 𝑉. 3. Se halla 𝑬 mediante 𝑬 = −𝛻𝑉 y 𝑫 mediante 𝑫 = 𝜀𝑬 4. Si se desea, se calcula 𝑄 inducida en un conductor mediante 𝑄 = 𝜌𝑠 𝑑𝑆, donde 𝜌𝑠 = 𝐷 𝑛 y 𝐷 𝑛 es la componente de 𝑫 normal al conductor. La capacitancia entre dos conductores 𝐶 = 𝑄/𝑉 fralbe.com
- 14. Ejemplo 1: Máquinafotocopiadora fralbe.com
- 15. Ejemplo 2: Planosconductores semiinfinitos fralbe.com
- 16. Ejemplo 3: Dosconos conductores de extensión infinita fralbe.com
- 17. Ejercicio 4: Potencialdependiente de 𝑥 y 𝑦 fralbe.com
- 18.
- 19. Resistencia El cálculode la resistencia de un conductor de sección transversal no uniforme puede considerarse un problema con valor en la frontera. Pasos para hallar la resistencia de un conductor: 1. Se elige el sistema de coordenadas apropiado. 2. Se presupone 𝑉0 como la diferencia de potencial entre las terminales del conductor. 3. Se resuelve la ecuación de Laplace 𝛻2 𝑉 para obtener 𝑉. Después se calcula 𝑬 a partir de 𝑬 = −𝛻𝑉 e 𝐼 a partir de 𝐼 = 𝜎𝑬 ∙ 𝑑𝑺. 4. Se obtiene 𝑅 como 𝑉0 𝐼 fralbe.com
- 20. Capacitor I Uncapacitor consta de dos (o más) conductores portadores de cargas iguales pero de signo contrario. Todas las líneas que salen de un conductor deben terminar necesariamente en la superficie del otro. Las placas (conductores) pueden estar separadas por el vacío o un dieléctrico. fralbe.com
- 21. Capacitor II Conductoresse mantiene a diferencia de potencial: 𝑬 es el campo eléctrico que existe entre conductores (normal a la superficie) fralbe.com
- 22. Capacitor III Lacapacitancia del capacitor es la razón de la magnitud de la carga en una de las placas a la diferencia de potencial entre ellas. La capacitancia 𝐶 es una propiedad física del capacitor, medida en farads (F). fralbe.com
- 23. Capacitor IV Métodospara obtener 𝐶 1. Se presupone 𝑄 y se calcula 𝑉 en términos de 𝑄 (implica ley de Gauss) 2. Se presupone 𝑉 y se calcula 𝑄 en términos de 𝑉 (implica ecuación de Laplace) Primer Método: Pasos 1. Se elige el sistema de coordenadas apropiado. 2. Se acepta que las dos placas conductoras portan cargas +𝑄 y −𝑄. 3. Se determina 𝑬 con base en la ley de Coulomb o de Gauss y se halla 𝑉 a partir de 𝑉 = 𝑬 ∙ 𝑑𝒍 . El signo negativo puede ignorarse en este caso, ya que lo que nos interesa es le valor absoluto de 𝑉. 4. Se obtiene 𝐶 a partir de 𝐶 = 𝑄/𝑉. fralbe.com
- 24. Ejemplo 1: Capacitorde placas paralelas Considere un capacitor de placas paralelas. Cada placa posee un área 𝑆 y que están separadas por una distancia 𝑑. Las placas 1 y 2 portan respectivamente cargas +𝑄 y − 𝑄 distribuidas de manera uniforme. Capacitor de placas paralelas Efecto de borde debido a un capacitor de placas paralelas fralbe.com
- 25. Ejemplo 1: Capacitorde placas paralelas Puede demostrarse que la energía almacenada en un capacitor está dada por: fralbe.com
- 26. Ejemplo 2: Capacitorcoaxial Considérese la longitud 𝐿 de los dos conductores coaxiales de radio interno 𝑎 y radio externo 𝑏 (𝑏 > 𝑎). El espacio entre los conductores está ocupado por un dieléctrico homogéneo con permitividad 𝜀. Los conductores 1 y 2 portan respectivamente +𝑄 y −𝑄 distribuidas de manera uniforme. fralbe.com
- 27. Ejemplo 2: Capacitorcoaxial fralbe.com
- 28. Ejemplo 3: Capacitoresférico Dos conductores esféricos concéntricos. Considérese la esfera interna de radio 𝑎 y la esfera externa de radio 𝑏 (𝑏 > 𝑎) separadas por un medio dieléctrico con permitividad 𝜀. Suponer cargas +𝑄 y −𝑄 en las esferas interna y externa, respectivamente. fralbe.com
- 29. Ejemplo 3: Capacitoresférico fralbe.com
- 30. Capacitores en Seriey Paralelo Capacitores en serie Capacitores en paralelo fralbe.com
- 31. Tiempo de relajación El producto de estas expresiones es el tiempo de relajación 𝑇𝑟 del medio que separa a los conductores. Válida para medios homogéneos fralbe.com
- 32. Tiempo de relajación Capacitor de placas paralelas Capacitor cilíndrico Capacitor esférico fralbe.com
- 33. Ejercicios Ejemplo 6.10,pág. 234 Ejercicio 6.10, pág 236 Ejemplo 6.12, pág 238 fralbe.com
- 34.
- 35. Método de imágenes Lateoría de las imágenes establece que una configuración de carga dada sobre un plano conductor perfecto e infinito conectado a tierra puede reemplazarse por la propia configuración de carga, su imagen y una superficie equipotencial en sustitución del plano conductor.fralbe.com
- 36. Método de imágenes Condicionespara aplicación del método de imágenes 1. La carga o cargas de imágenes deben situarse en la región conductora. 2. La carga o cargas de imágenes deben situarse de tal forma que en la superficie o superficies conductoras el potencial sea de cero o constante. fralbe.com
- 37. Carga puntual sobreun plano conductor a tierra El campo eléctrico en el punto 𝑃(𝑥, 𝑦, 𝑧): fralbe.com
- 38. Carga puntual sobreun plano conductor a tierra fralbe.com
- 39. Carga puntual sobreun plano conductor a tierra fralbe.com
- 40.
- 41. Bibliografía y Referencias Sadiku, Matthew N. O. «Elementos de Electromagnetismo», Editorial Alfaomega, Oxford University Press, 2010. fralbe.com
- 42. Esta obra estabajo licencia Creative Commons de Reconocimiento, No Comercial y Sin Obras Derivadas, Ecuador 3.0 www.creativecommons.org www.fralbe.com fralbe.com