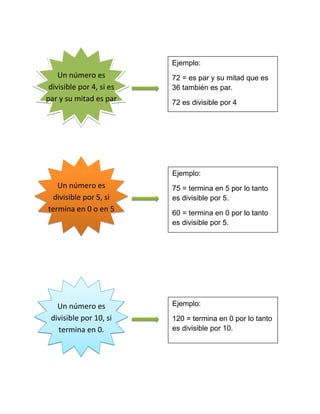
El documento explica conceptos matemáticos como múltiplos, divisores, mínimo común múltiplo y máximo común divisor de números. Define los múltiplos de un número como los resultados de multiplicarlo por los números naturales. Explica cómo calcular el mínimo común múltiplo y el máximo común divisor mediante la descomposición de los números en factores primos.

1. MULTIPLOS DE UN NÚMERO
Los múltiplos de un número son el conjunto de los números que se
obtienen al multiplicarlo por los números naturales incluyendo el cero.
Por ejemplo: los múltiplos de 4 se obtienen así:
M4={4X 0 , 4 X 1 , 4 X 2, 4 X 3, 4 X 4, 4 X 5, 4 X 6, ...}
M4 = {0,4, 8,12, 16, 20, 24,...}
M4 representa el conjunto de los múltiplos de 4.
Los puntos
suspensivos indican
que el conjunto tiene
más elementos.
Ejemplo:
Ahora vamos a escribir los múltiplos de 3. Y nos quedaría así:
M3 = {0,3, 6, 9, 12, 15, 18, 21, 24,...}
DEBES COMPRENDER QUE:
El conjunto de los múltiplos de un número es infinito.
Se simboliza con la letra M y el número, así: el conjunto “múltiplos de
12” se escribe M12.y se puede representar así:
M4= {0,12, 24, 36, 48, 60,...}
Ejercicio de análisis:
Los yogures que produce una industria láctea se venden en paquetes
de cuatro o de seisunidades. ¿Cuántos yogures pueden vender en un
día?
• Para calcular la cantidad de yogures que pueden vender se buscan
los múltiplos de 4 y de 6.
• Para hacerlo, se multiplican 4 y 6 por cada uno de los números
naturales: 0, 1, 2, 3, 4, 5, ...

2. X0
X1
X2
X3
X4
X5
Múltiplos de 4
0
4
8
12
16
…
Múltiplos de 6
0
6
12
18
24
…
Rta: Pueden vender cuatro, ocho, doce, 16 … yo g u r e s e n
p a q u e t e s d e c u a t r o , o s e i s , doce, 18, 24... yogures en paquetes
de seis.
• Los números 0, 4, 8, 12, 16... son múltiplos de 4.
• Los números 0, 6, 12, 18, 24... son múltiplos de 6.
DIVISORES DE UN NÚMERO
Los divisores de un número son aquellos números que lo dividen
exactamente.
Por ejemplo, para encontrar los divisores de 8 se divide 8 entre los
números naturales menores o iguales que 8
8 1
8 2
8
3
8
4
0 8
0
4
2
2
0
2
8 5
8 6
8
7
8
8
3
2
1
1
0
1
1
1
Hay que tener en cuenta que las divisiones entre 1, 2, 4 y 8 son
exactas.
El conjunto de los divisores de 8 se nombra D8, así:
D8 = {1, 2, 4, 8. }

3. PARA RECORDAR:
Un número es divisor de otro si al hacer la división el residuo es cero.
El conjunto de los divisores de un número es finito.
Se simboliza con la letra D y el número.
El conjunto de los divisores de 24 se escribe D24
Se puede representar así
D24= {1, 2, 3, 4, 6, 8, 12, 24}
CRITERIOS DE DIVISIBILIDAD
Los criterios de divisibilidad son reglas que permiten saber si un
número es divisible entre otro para hacer la división.
Un número es
divisible entre 2 si
termina en 0 o en
cifra par.
Un número es
divisible entre 3, si al
sumar sus cifras el
resultado es múltiplo
de 3
Ejemplo:
48= 4+8=12 es divisible por 2
Ejemplo:
405 = 4 + 0 + 5 = 9
9 es múltiplo de 3

4. Ejemplo:
Un número es
divisible por 4, si es
par y su mitad es par
72 = es par y su mitad que es
36 también es par.
72 es divisible por 4
Ejemplo:
Un número es
divisible por 5, si
termina en 0 o en 5
Un número es
divisible por 10, si
termina en 0.
75 = termina en 5 por lo tanto
es divisible por 5.
60 = termina en 0 por lo tanto
es divisible por 5.
Ejemplo:
120 = termina en 0 por lo tanto
es divisible por 10.

5. PARA COMPRENDER:
Los criterios de divisibilidad permiten identificar fácilmente cuando un
número es divisible por otro.
• 570 es divisible por 2 porque termina en cero.
• 570 es divisible por 3 porque la suma de sus cifras (5 + 7 + 0 =
12) es un múltiplo de 3.
• 570 es divisible por 5 porque termina en cero.
• 570 es divisible por 10 porque termina en cero.
NÚMEROS PRIMOS Y COMPUESTOS
De acuerdo con la cantidad de divisores un número puede ser primo o
compuesto.
PRIMO:Si tiene únicamente dos divisores distintos, el 1 y él mismo.
COMPUESTO: Si tiene más de dos divisores.
El 1 no es ni primo ni compuesto ya que tiene un único divisor que es
él mismo.
DESCOMPOSICION EN FACTORES PRIMOS
Todo número compuesto se puede expresar como un producto de
números primos; por ejemplo:
12
2 x
2 y 3 son números primos.
6
2
Luego 12= 2 x 2 x 3
3

6. Para descomponer un número en factores primos, se puede utilizar el
procedimiento de divisiones sucesivas con divisores primos. Así:
90 es divisible entre 2
90 ÷ 2 = 45
90
2
45 es divisible entre 3
45 ÷ 3 = 15
45
3
15 es divisible entre 3
15 ÷ 3 = 5
15
3
5 es divisible entre 5
5÷5= 1
5
5
1
El procedimiento termina cuando la última división tiene cociente 1.
Entonces: 90 = 2 x 3 x 3 x 5
Realizaremos el siguiente ejercicio:
Elías tiene 18 rosas y quiere hacer
arreglos florales de más de una flor y
con igual cantidad de flores, ¿de
cuántas maneras las puede organizar?
• Para saber las diferentes maneras de
organizar los ramilletes de flores se
descompone 18 en sus factores
primos.
Árbol de factores
18
2 x 9
3
x
3

7. La división anterior también se puede hacer así:
18
2
9
3
3
3
1
MÍNIMO COMÚN MÚLTIPLO
El mínimo común múltiplo (m. c. m.) de dos o más números es el
menor de sus múltiplos comunes, distinto de cero.
Por ejemplo: el mcm entre 4 y 6 se halla así:
M4 = {0, 4, 8, 12, 16, 20, 24, 28, ….}
M6 = {0, 6, 12, 18, 24, 30, 36, 42, ….}
Al hablar de múltiplos comunes se busca la intersección entre los
conjuntos. Es decir,
M4 ∩M6 = {0, 12, 24}
Por lo tanto el mcm (4,6) = 12
MÁXIMO COMÚN DIVISOR
El máximo común divisor (m. c. d.) de dos o más números es el mayor
de los divisores comunes de esos números.
Por ejemplo: el mcd entre 20 y 16 se busca así:

8. D20 = {1, 2, 4, 5, 10, 20 }D16 = {1, 2, 4, 8, 16 }
D20 ∩D16 = {1, 2, 4}
El mayor número que divide a 20 y a 16 es 4. Luego el mcd (20,16)= 4.
CALCULO DEL MAXIMO COMUN DIVISOR POR
DESCOMPOSICIÓN
Para calcular el máximo común divisor de dos o más números. Se
descomponen en sus factores primos comunes así:
Son divisibles entre 2
24
30
2
Son divisibles entre 3
12
15
3
4
5
El mcd (24,30) = 6
Cómo no hay otro número que divida a 4 y a 5, el máximo común
divisor entre 24 y 30, es 2 x 3, es decir, 6.
PARA RECORDAR:
El mínimo común múltiplo (m. c. m.) se puede calcular mediante el
siguiente proceso:
Se descomponen los números en sus factores primos
Se expresan los factores hallados como potencias.
Se busca el producto de los factores comunes y no comunes
con el mayor exponente

9. PARA RECORDAR:
El máximo común divisor (m. c. d.) se puede calcular
mediante el siguiente proceso:
Se descomponen los números en sus factores primos.
Se expresan los factores hallados como potencias.
Se busca el producto de los factores comunes con el
menorexponente.
Realizaremos el siguiente ejemplo:
Ana, Patricia y Luis entrenan en el
polideportivo. Ana patina cada dos días,
Eva nada cada tres y Luis juega tenis cada
cuatro.
Hoy coincidieron en sus entrenamientos.
¿Cuándo volverán a hacerlo?
• Para averiguarlo, se busca el menor de
los múltiplos comunes de 2, 3 y 4,
también llamado mínimo común múltiplo,
que coinciden con los múltiplos de 2, 3, y
4. Se resaltan los múltiplos comunes y se
elige elmenor.
Días que entrena Ana: 2, 4, 6, 8, 10, 12, 14, 16,18, 20, 22, 24, 26...
Días que entrena Patricia:3.6.9.12.15,18,21, 24, 27, 30, 33...
Días que entrenaLuis:4, 8, 12,16, 20. 24, 28, 32, 36, 40...
R/ Como el menor de los múltiplos comunes es 12, los tres amigos
coinciden cada doce días en el polideportivo.
Puedes afianzar los conocimientos realizando las actividades.