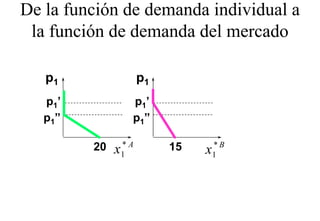
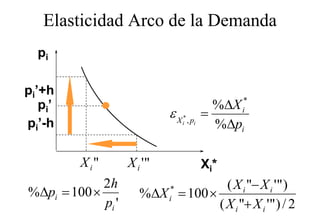
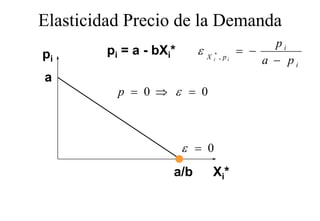
El documento resume los conceptos fundamentales de la demanda de mercado y la elasticidad. Explica que la demanda de mercado es la suma horizontal de las demandas individuales de los consumidores. También define la elasticidad como una medida de la sensibilidad de una variable ante cambios en otra variable, y analiza la elasticidad precio de la demanda en particular.

1. Módulo 7
LA DEMANDA DE MERCADO

2. De la función de demanda individual a
la función de demanda del mercado
Pensemos en una economía con n
consumidores i = 1 … ,n
id 1,
La demanda marshalliana del i-ésimo
consumidor por el bien j es,
*i i
x ( p1, p2 , m )
j

3. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
Si todos los consumidores son tomadores de
precios, entonces la demanda del mercado
por el bi j es
l bien
n
X j ( p1, p2 , m ,L, m ) = ∑ x ( p1, p2 , m ).
1 n *i
j
i
i =1
Si todos los consumidores son idénticos
idénticos,
entonces
X j ( p1, p2 , M ) = n × x ( p1, p2 , m)
*
j
donde M = nm

4. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
La curva de demanda del mercado es la
“suma horizontal” de las curvas de demanda
suma horizontal
individuales
Por ejemplo, supongamos que sólo se tienen
dos consumidores en la economía; i = A,B

5. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
p1 p1
p1’ p1’
p1” p1”
20 *A 15 *B
x 1 x 1

6. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
p1 p1
p1’ p1’
p1” p1”
20 *A
x 15 *B
x
p1 1 1
p1’
x +x
*A
1
B
1

7. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
p1 p1
p1’ p1’
p1” p1”
20 *A
x 15 *B
x
p1 1 1
p1’
p1”
x +x
*A
1
B
1

8. De la función de demanda individual a
la f ió d d
l función de demanda del mercado
d d l d
p1 p1
p1’ p1’
p1” p1”
20 *A
x 15 x*B
p1 1 1
p1’ La “suma horizontal”
de las curvas de
p1” demanda de A y B
35
x +x
*A
1
B
1

9. Elasticidades
Mide la “sensibilidad” de una variable en
relación a otra
La elasticidad de la variable x en relación a
la variable y es,
% ∆x
ε x,y = .
% ∆y

10. Aplicaciones de la Elasticidad
p
Los economistas emplean la elasticidad
como medida de la sensibilidad de
La
L cantidad d
tid d demandada d l bi i
d d del bien
respecto a su precio (elasticidad precio de
demanda)
La demanda del bien i en relación al
precio del bien j (elasticidad precio
cruzada d d
d de demanda) d )

11. Aplicaciones de la Elasticidad
p
La demanda por el bien i en relación al
ingreso (elasticidad ingreso de demanda)
La cantidad ofrecida del bien i respecto a
su precio (elasticidad precio de oferta)
p ec o (e ast c dad p ec o o e ta)

12. Aplicaciones de la Elasticidad
p
La cantidad ofrecida del bien i en
relación al salario (elasticidad de oferta
en relación al salario)
Y muchas, muchas otras situaciones

13. Elasticidad precio de demanda
p
Pregunta: ¿Por qué no empleamos la
pendiente de la curva de demanda como
medida de la sensibilidad de la cantidad
demandada frente a un cambio en el precio?
n

14. Elasticidad precio de demanda
p
p1 p1
Pendiente Pendiente
10 =-2 10 = - 0.2
5 X 1* 50 X *
1
¿en cuál de estos casos la cantidad demandada es
más sensible al cambio en el precio?

15. Elasticidad precio de demanda
p
p1 p1
Pendiente Pendiente
10 =-2 10 = - 0.2
5 X 1* 50 X *
1

16. Elasticidad precio de demanda
p
decenas unidades
p1 p1
Pendiente Pendiente
10 =-2 10 = - 0.2
5 X 1* 50 X *
1

17. Elasticidad precio de demanda
p
decenas unidades
p1 p1
Pendiente Pendiente
10 =-2 10 = - 0.2
5 X 1* 50 X *
1
La cantidad demandada es igual de sensible en los
dos casos

18. Elasticidad precio de demanda
p
Respuesta: debido a que el valor de la
sensibilidad,
sensibilidad depende de las unidades de
medida empleadas

19. Elasticidad precio de demanda
p
% ∆x *
εx * = 1
1 , p1
% ∆ p1
En t
E este caso l medida d l sensibilidad es una
la did de la ibilid d
tasa de porcentajes y no depende de las unidades
de medida

20. Elasticidad Arco y elasticidad p
punto
La elasticidad precio “promedio” de
demanda del bien i sobre un intervalo de
precios se conoce como elasticidad arco, y
g
generalmente se estima mediante la fórmula
del punto medio
La elasticidad estimada para un único valor
del precio se conoce como elasticidad punto

21. Elasticidad Arco de la Demanda
pi ¿Cúal es l elasticidad
Cú l la l i id d
precio “promedio” de demanda
pi’+h para el i
l intervalo d precios
l de i
p i’ centrado en pi’?
pi’-h
X i*

22. Elasticidad Arco de la Demanda
pi
pi’+h
p i’
pi’-h
X i" X i '" X i*

23. Elasticidad Arco de la Demanda
pi
pi’+h
p i’ % ∆ X i*
εX * =
pi’-h i , pi
% ∆ pi
X i" X i '" X i*

24. Elasticidad Arco de la Demanda
pi
pi’+h
p i’ % ∆X *
εX * = i
pi’-h i , pi
% ∆pi
X i" X i '" X i*
2h
% ∆pi = 100 ×
pi '

25. Elasticidad Arco de la Demanda
pi
pi’+h
p i’ %∆X *
εX * = i
pi’-h i , pi
%∆pi
Xi" X i '" X i*
2h ( X i "− X i '" )
%∆pi = 100 × %∆X = 100 ×
*
i
pi ' ( X i "+ X i '" ) / 2

26. Elasticidad Arco de la Demanda
2h
% ∆ p i = 100 ×
% ∆ X i* pi '
εX * =
i , pi
% ∆ pi
( X i "− X i ' " )
% ∆X i
*
= 100 ×
( X i "+ X i ' " ) / 2

27. Elasticidad Arco de la Demanda
2h
% ∆ pi = 100 ×
% ∆X *
pi '
εX * = i
i , pi
% ∆ pi
( X i "− X i ' " )
% ∆ X = 100 ×
*
i
( X i "+ X i ' " ) / 2
% ∆X *
pi ' ( X i "− X i ' " )
εX * = =i
× .
i , pi
% ∆ pi ( X i "+ X i ' " ) / 2 2h
Esta es la elasticidad arco para el intervalo de precios
p p
centrado en pi’

28. Elasticidad Precio de la Demanda
pi
¿Cuál es la elasticidad precio
de demanda dentro de un
pi’+h muy pequeño intervalo
p i’ de precios centrado en pi’?
?
pi’-h
X i" X i '" X i*
% ∆X i*
pi ' ( X i "− X i ' " )
εX * = = × .
i , pi
% ∆ pi ( X i "+ X i ' " ) / 2 2h

29. Elasticidad Precio de la Demanda
pi
pi’+h h → 0,
p i’
pi’-h
X i" X i '" X i*
% ∆X *
pi ' ( X i "− X i ' " )
εX * = =i
× .
i , pi
% ∆ pi ( X i "+ X i ' " ) / 2 2h

30. Elasticidad Precio de la Demanda
pi
pi’+h h → 0,
p i’
pi’-h
X i" X i '" X i*
% ∆X *
pi ' ( X i "− X i ' " )
εX * = =i
× .
i , pi
% ∆ pi ( X i "+ X i ' " ) / 2 2h

31. Elasticidad Precio de la Demanda
pi
pi’+h h → 0,
p i’
pi’-h
X i' X i*
% ∆ X i* pi ' ( X i "− X i ' " )
εX * = = × .
i , pi
% ∆ pi ( X i "+ X i ' " ) / 2 2h

32. Elasticidad Precio de la Demanda
pi
h → 0,
p i’ p i ' dX i*
εX * → ×
i , pi
X i ' dp i
Xi' X i*
%∆X *
pi ' ( X i "− X i '" )
εX * = = i
× .
i , pi
%∆pi ( X i "+ X i '" ) / 2 2h

33. Elasticidad Precio de la Demanda
pi
*
p i ' dX
ε X *
, pi
= × i
p i’
i
X i' dp i
Esta es la elasticidad en el punto
( X i ', pi ')
).
X i' X i*

34. Elasticidad Precio de la Demanda
*
pi dXi
ε X*, p = * ×
i i
Xi dpi
Por j
P ejemplo, supongamos que pi = a - bXi.
l
Xi = (a-pi)/b y
*
dX 1 Entonces,
i
=− .
dpi b
pi  1 pi
ε Xi*, pi = × −  = − .
(a − pi ) / b  b  a − pi

35. Elasticidad Precio de la Demanda
pi pi = a - bXi*
a
a/b X i*

36. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* εX * =−
i , pi
a − pi
a
a/b X i*

37. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* εX * = −
i , pi
a − pi
a
p=0⇒ε =0
a/b X i*

38. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* ε * = −
X i , pi
a − pi
a
p = 0 ⇒ ε = 0
ε = 0
a/b X i*

39. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* εX * = −
i , pi
a − pi
a a a/2
p = ⇒ε = − = −1
2 a−a/2
ε =0
a/b X i*

40. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* ε * = −
X i , pi
a − pi
a a a/2
p= ⇒ε =− = −1
2 a−a/2
a/2
/2 ε = −1
ε = 0
a/2b a/b X i*

41. Elasticidad Precio de la Demanda
pi
pi = a - bXi* ε = −
pi X *
i , pi
a − pi
a a
p =a⇒ ε =− = −∞
a−a
a/2
/2 ε = −1
ε = 0
a/2b a/b X i*

42. Elasticidad Precio de la Demanda
pi
pi = a - bXi* ε = −
pi X *
i , pi
a − pi
a ε = −∞ a
p = a ⇒ ε = − = −∞
a−a
a/2
/2 ε = −1
ε = 0
a/2b a/b X i*

43. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* εX * = −
i , pi
a − pi
a ε = −∞∞
elástico
a/2
/2 ε = −1
inelástico
ε = 0
a/2b a/b X i*

44. Elasticidad Precio de la Demanda
pi
pi pi = a - bXi* ε * = −
X i , pi
a − pi
a ε = −∞
elástico
a/2
/2 ε = − 1 ( l ti id d unitaria)
(elasticidad it i )
inelástico
ε = 0
a/2b a/b X i*

45. Elasticidad Precio de la Demanda
*
pi dX
εX ,p
* = *× i
Por ejemplo
i i
Xi dpi
*
X = kp .
* a dX a −1
i i
Entonces i
= a pi
dp
d i
a
pi p
εX ,p
*
a−1
= a × kapi = a = a. i
a
i i
kpi p i

46. Elasticidad Precio de la Demanda
pi −2 k
Xi = k i = k i = 2
* a
kp kp
pi
ε = −2 a lo largo de toda
la curva de demanda
X i*

47. El ingreso y la elasticidad precio de
demanda
d d
Si al subir el precio se provoca una
disminución pequeña en la cantidad
demandada, entonces el ingreso del
vendedor se incrementa
endedor
Cuando la demanda es inelástica el ingreso
g
de los vendedores se incrementa cuando el
precio se incrementa

48. El ingreso y la elasticidad precio de
demanda
d d
Si al subir el precio se provoca una gran
disminución en la cantidad demandada
demandada,
entonces el ingreso de los vendedores se
reduce
red ce
Cuando la demanda es elástica el ingreso de
g
los vendedores cae cuando el precio se
incrementa

49. El ingreso y la elasticidad precio de
demanda
d d
El ingreso de los vendedores es:
I ( p) = p × X ( p).
*

50. El ingreso y la elasticidad precio de
demanda
d d
*
dI dX
= X ( p) + p
*
dp dp
Entonces
*
dR dX
= X ( p) + p
*
dp dp
 p dX 
*
= X ( p) 1 + *
*

 X ( p) dp 

51. El ingreso y la elasticidad precio de
demanda
d d
= X * ( p ) [ + ε ].
1
dR
= X * ( p )[ + ε
1 ]
dp
si ε = −1 entonces dR = 0
dp
Y un cambio en el ingreso no altera los
ingresos de los vendedores

52. El ingreso y la elasticidad precio de
demanda
d d
si ε = −1 dI
= 0
dp
d
Y un cambio en el ingreso no altera los
ingresos de los vendedores

53. El ingreso y la elasticidad precio de
demanda
d d
dI
Pero si − 1 < ε ≤ 0 > 0
dp
Un incremento en el precio aumenta los ingresos
de los vendedores

54. El ingreso y la elasticidad precio de
demanda
d d
dI
Y si ε < −1 <0
dp
Y un incremento en el precio reduce los ingresos
de los vendedores

55. Ingreso Marginal y Elasticidad Precio
de D
d Demanda d
El ingreso marginal es la tasa a la cual
cambia el ingreso del vendedor con el
número de unidades vendidas
dI (q)
IM (q) =
IMg .
dq

56. Ingreso Marginal y Elasticidad Precio
de D
d Demanda d
p(q) es l f ió i
( ) la función inversa d d
de demanda
d
I (q) = p(q) × q
dI (q) dp(q)
IMg(q) = = q + p(q)
dq dq
 q d (q) 
dp
= p(q)1 + .
 p(q) dq 

57. Ingreso Marginal y Elasticidad Precio
de D
d Demanda d
 q d (q) 
dp
IMg(q) = p(q)1+ .
 p(q) dq 
y dq
d p
ε= ×
dp q
 1
IMg(q) = p(q)1+ .
 ε

58. Ingreso Marginal y Elasticidad Precio
de D
d Demanda d
 1
IMg ( q ) = p ( q ) 1 + 
 ε
Nos dice que la tasa la cual cambia
el ingreso del vendedor con el número de
unidades que vende dependen de la
q p
sensibilidad de la cantidad demandada al
precio,
precio es decir depende de la elasticidad
precio de demanda

59. Ingreso Marginal y Elasticidad
Precio de Demanda
 1
IMg q) = p(q)1+ 
(
 ε
Si ε = −1 IMg ( q ) = 0 .
Si −1 < ε ≤ 0 IMg ( q ) < 0 .
Si ε < −1 IM ( q ) > 0 .
IMg

60. Ingreso Marginal y Elasticidad Precio
de Demanda
d D d
p Veamos el caso de una función inversa de
demanda lineal
a
p ( q ) = a − bq
a/2b a/b q
IMg ( q ) = a − 2 bq

61. Ingreso Marginal y Elasticidad Precio
p de Demanda
d D d
a
IMg ( q ) = a − 2bq
p(q) = a − bq
$ a/2b a/b q
I(q)
a/2b a/b q