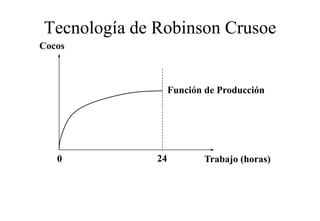
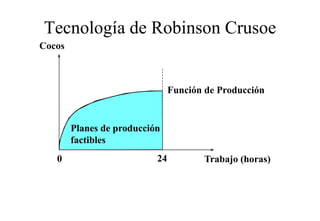
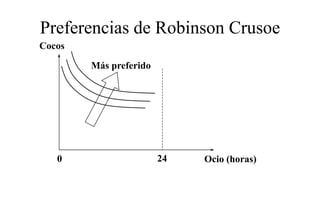
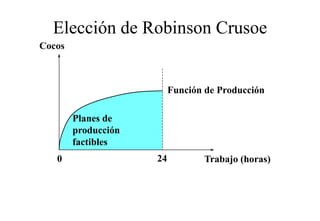
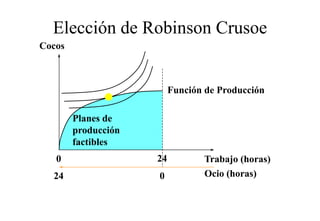
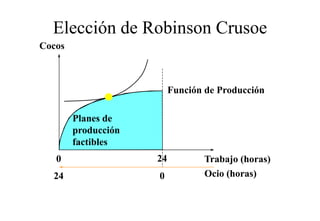
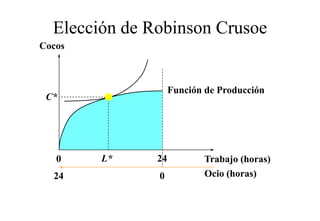
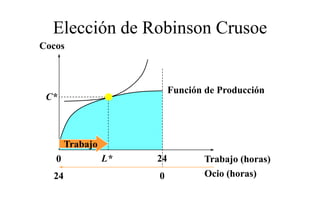
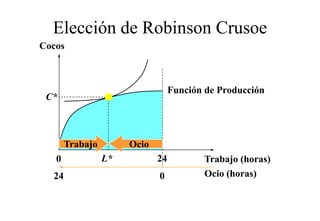
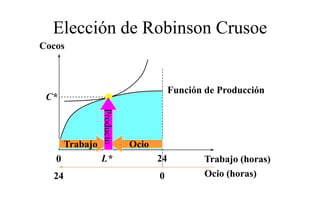
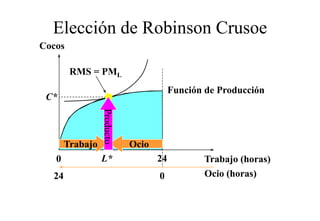
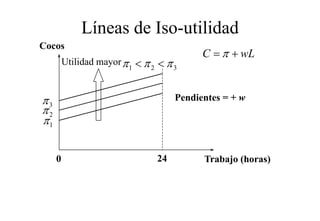
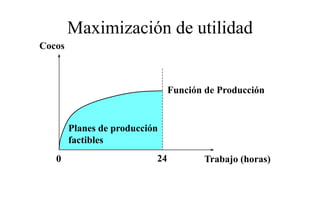
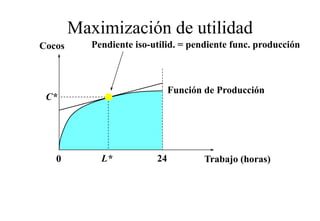
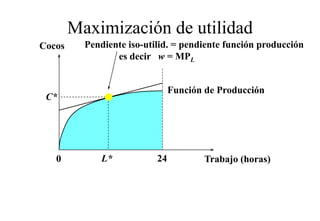
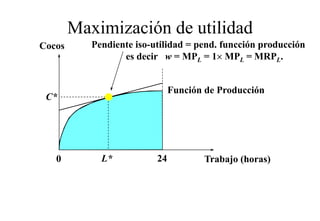
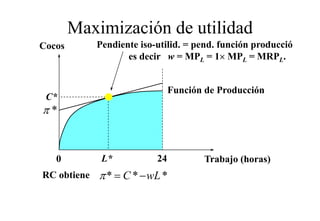
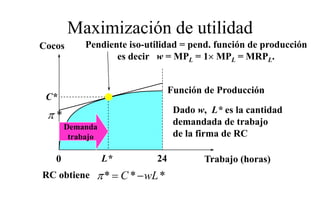
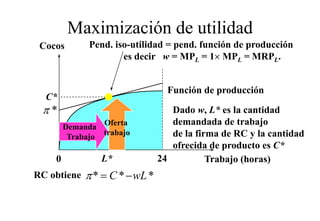
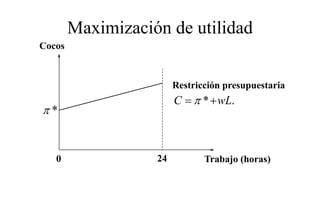
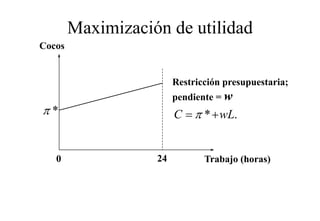
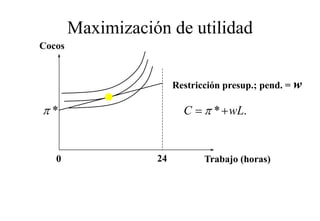
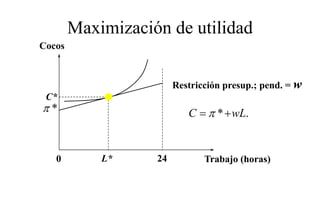
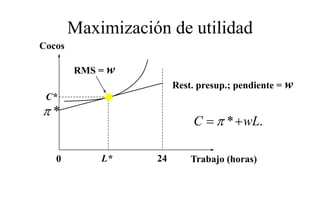
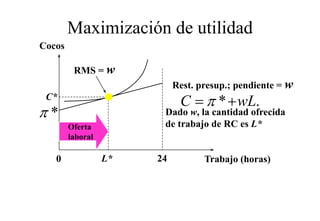
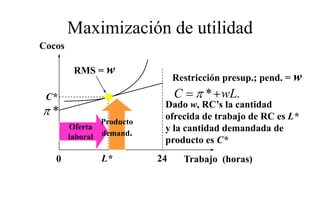
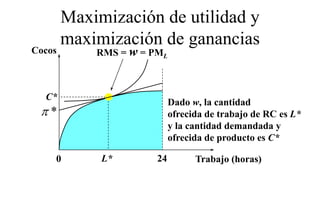
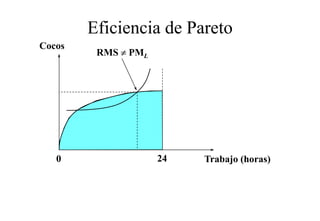
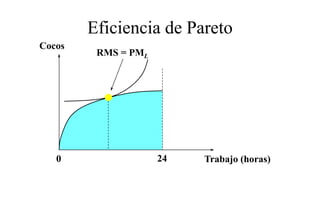
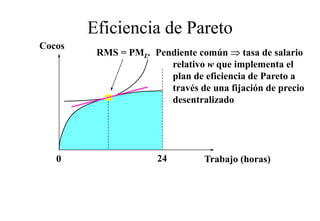
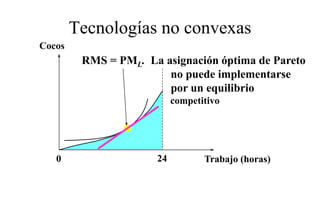
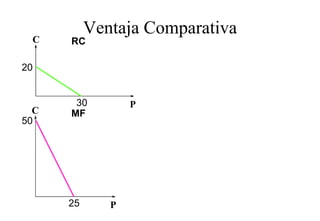
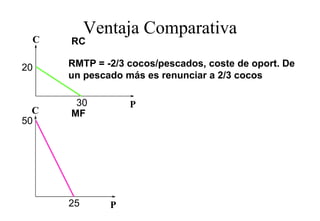
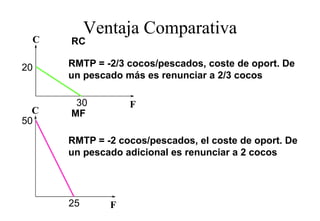
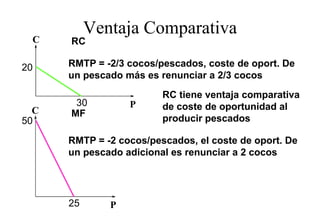
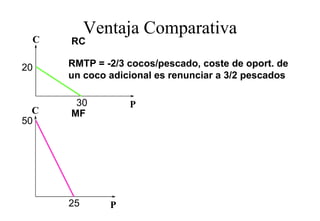
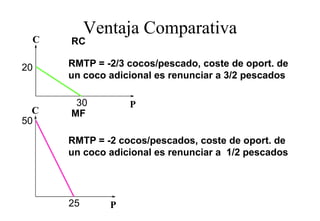
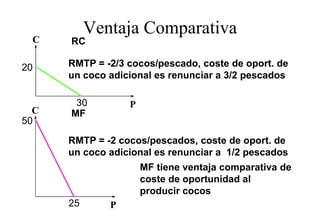
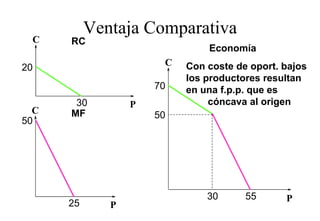
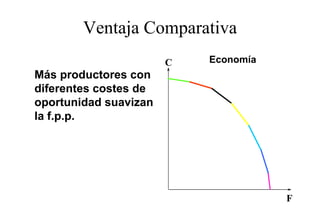
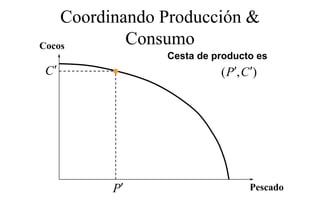
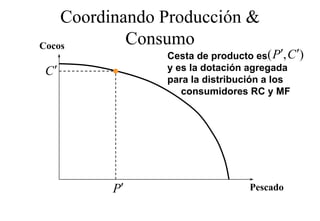
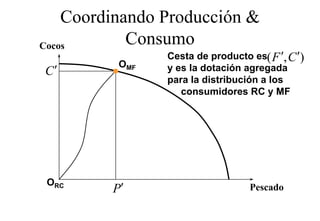
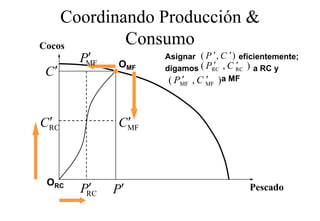
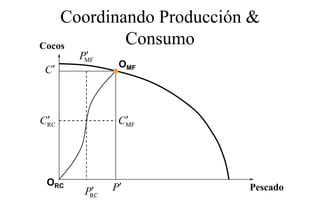
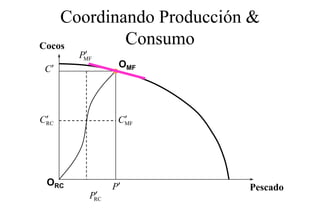
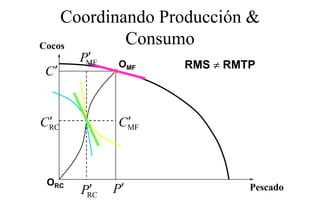
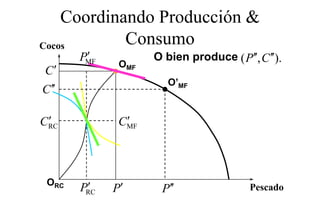
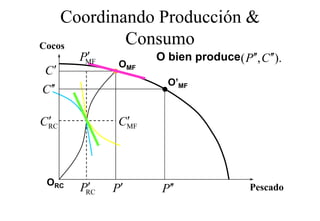
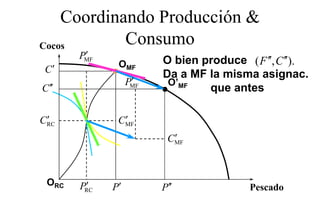
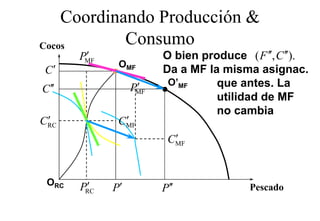
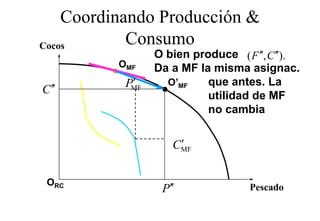
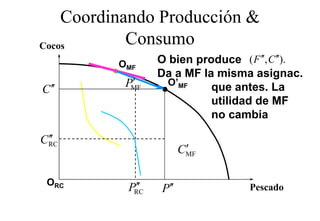
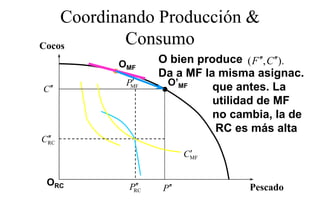
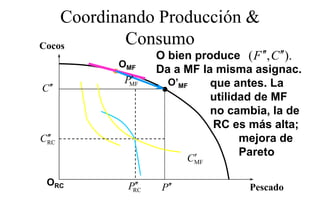
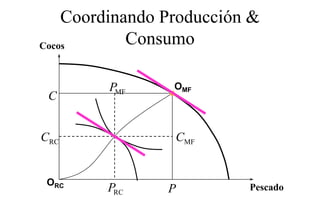
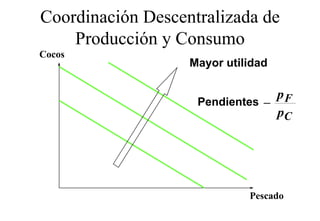
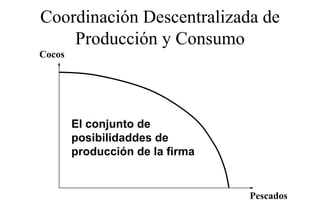
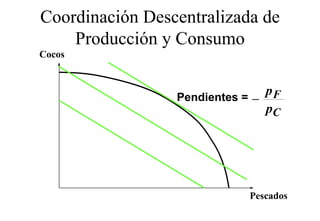
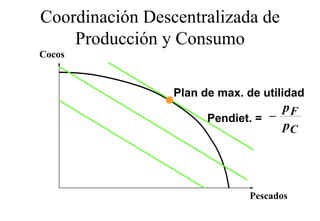
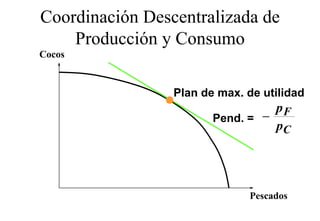
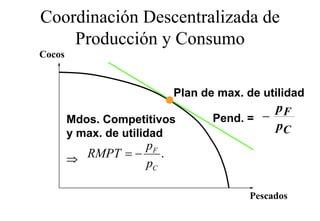
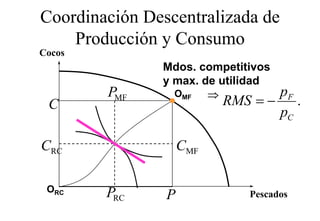
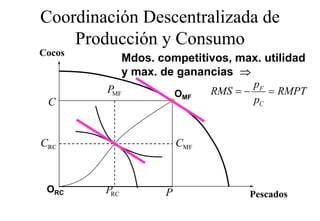
Este documento describe el modelo de Robinson Crusoe para analizar la elección entre trabajo y ocio de un agente. Explica que Robinson Crusoe tiene 24 horas para trabajar y producir cocos o disfrutar del ocio. Maximiza su utilidad eligiendo el nivel de trabajo L* que iguala su salario w con el producto marginal del trabajo, logrando el máximo de cocos C* y utilidad π*.

1. Módulo 14
Eficiencia y Producción

2. Economía de Robinson Crusoe
Un agente, RC
Dotado con una cantidad fija de un
recurso -- 24 horas
Usa el tiempo para trabajo
(producción) u ocio (consumo)
Tiempo trabajo = L. Tiempo ocio =
24 - L
¿
¿Qué escogerá RC?
g

3. Tecnología de Robinson Crusoe
Tecnología: el trabajo produce un
bien (cocos) de acuerdo a la función
de producción cóncava

4. Tecnología de Robinson Crusoe
Cocos
Función de Producción
0 24 Trabajo (horas)

5. Tecnología de Robinson Crusoe
Cocos
Función de Producción
Planes de producción
factibles
f tibl
0 24 Trabajo (horas)

6. Preferencias de Robinson Crusoe
Preferencias de RC:
– coco es un bien
– ocio es un bien

7. Preferencias de Robinson Crusoe
Cocos
Más preferido
0 24 Ocio (horas)

8. Preferencias de Robinson Crusoe
Cocos
Más preferido
24 0 Ocio (horas)

9. Elección de Robinson Crusoe
Cocos
Función de Producción
Planes de
producción
factibles
0 24 Trabajo (horas)

10. Elección de Robinson Crusoe
Cocos
Función de Producción
Planes de
producción
factibles
0 24 Trabajo (horas)
24 0 Ocio (horas)

11. Elección de Robinson Crusoe
Cocos
Función de Producción
Planes de
producción
factibles
0 24 Trabajo (horas)
24 0 Ocio (horas)

12. Elección de Robinson Crusoe
Cocos
Función de Producción
Planes de
producción
factibles
0 24 Trabajo (horas)
24 0 Ocio (horas)

13. Elección de Robinson Crusoe
Cocos
Función de Producción
C*
0 L* 24 Trabajo (horas)
24 0 Ocio (horas)

14. Elección de Robinson Crusoe
Cocos
Función de Producción
C*
Trabajo
0 L* 24 Trabajo (horas)
24 0 Ocio (horas)

15. Elección de Robinson Crusoe
Cocos
Función de Producción
C*
Trabajo Ocio
0 L* 24 Trabajo (horas)
24 0 Ocio (horas)

16. Elección de Robinson Crusoe
Cocos
Función de Producción
C* P
Product
to
Trabajo Ocio
0 L* 24 Trabajo (horas)
24 0 Ocio (horas)

17. Elección de Robinson Crusoe
Cocos
RMS = PML
Función de Producción
C* P
Product
to
Trabajo Ocio
0 L* 24 Trabajo (horas)
24 0 Ocio (horas)

18. Robinson Crusoe como una
Firma
Supongamos que RC es consumidor
maximizador de utilidad y empresa
maximizadora de utilidad
Usamos l cocos como el bien
U los l bi
numerario; es decir precio de un
coco = $1
Salario de RC es w
Nivel de producto de coco es C

19. Robinson Crusoe como una
Firma
Utilidad de RC como firma es π = C -
wL
π = C - wL ⇔ C = π + wL, la ecuación
de
d una línea de iso-utilidad
lí d i ilid d
Pendiente = + w
Intercepto = π

20. Líneas de Iso utilidad
Iso-utilidad
Cocos
C = π + wL
Utilidad mayor π < π < π
1 2 3
π3 Pendientes = + w
π2
π1
0 24 Trabajo (horas)

21. Maximización de utilidad
Cocos
Función de Producción
Planes de producción
factibles
f tibl
0 24 Trabajo (horas)

22. Maximización de utilidad
Cocos
Función de Producción
0 24 Trabajo (horas)

23. Maximización de utilidad
Cocos
Función de Producción
0 24 Trabajo (horas)

24. Maximización de utilidad
Cocos
Función de Producción
C*
0 L* 24 Trabajo (horas)

25. Maximización de utilidad
Cocos Pendiente iso-utilid. = pendiente func. producción
Función de Producción
C*
0 L* 24 Trabajo (horas)

26. Maximización de utilidad
Cocos Pendiente iso-utilid. = pendiente función producción
es decir w = MPL
Función de Producción
C*
0 L* 24 Trabajo (horas)

27. Maximización de utilidad
Cocos Pendiente iso-utilidad = pend. funcción producción
es decir w = MPL = 1× MPL = MRPL.
Función de Producción
C*
0 L* 24 Trabajo (horas)

28. Maximización de utilidad
Cocos Pendiente iso-utilid. = pend. función producció
es decir w = MPL = 1× MPL = MRPL.
Función de Producción
C*
π*
0 L* 24 Trabajo (horas)
RC obtiene π * = C * − wL *

29. Maximización de utilidad
Cocos Pendiente iso-utilidad = pend. función de producción
es decir w = MPL = 1× MPL = MRPL.
Función de Producción
C*
Dado w L* es la cantidad
w, L
π*
Demanda
demandada de trabajo
trabajo de la firma de RC
0 L* 24 Trabajo (horas)
RC obtiene π * = C * − wL *

30. Maximización de utilidad
Cocos Pend. iso-utilidad = pend. función de producción
es decir w = MPL = 1× MPL = MRPL.
Función de producción
C*
π* Dado w L* es la cantidad
w, L
Demanda
Oferta demandada de trabajo
Trabajo
trabajo de la firma de RC y la cantidad
ofrecida de producto es C*
0 L* 24 Trabajo (horas)
RC obtiene π * = C * − wL *

31. Maximización de utilidad
Ahora consideremos a RC como un
consumidor con una dotación $π*
que puede trabajar por $w por hora
¿Cuál es l cesta de consumo
C ál la d
preferida de RC?
La restricción presupuestaria es
C = π * + wL.

32. Maximización de utilidad
Cocos
Restricción
R t i ió presupuestaria
t i
C = π * + wL.
π*
0 24 Trabajo (horas)

33. Maximización de utilidad
Cocos
Restricción presupuestaria;
pendiente = w
π* C = π * + wL.
L
0 24 Trabajo (horas)

34. Maximización de utilidad
Cocos
Más preferido
0 24 Trabajo (horas)

35. Maximización de utilidad
Cocos
R t presupuest.; pendient. = w
Rest. t di t
π* C = π * + wL.
0 24 Trabajo (horas)

36. Maximización de utilidad
Cocos
R t i ió presup.; pend. = w
Restricción d
π* C = π * + wL.
0 24 Trabajo (horas)

37. Maximización de utilidad
Cocos
R t i ió presup.; pend. = w
Restricción d
C*
π* C = π * + wL.
L
0 L* 24 Trabajo (horas)

38. Maximización de utilidad
Cocos
RMS = w
R t presup.; pendiente = w
Rest. di t
C*
π*
C = π * + wL.
0 L* 24 Trabajo (horas)

39. Maximización de utilidad
Cocos
RMS = w
R t presup.; pendiente = w
Rest. di t
C*
C = π * + wL.
π* Dado w, la cantidad ofrecida
Oferta de trabajo de RC es L*
laboral
0 L* 24 Trabajo (horas)

40. Maximización de utilidad
Cocos
RMS = w
p pend. = w
Restricción presup.; p
p
C* C = π * + wL.
Dado w, RC’s la cantidad
π* ofrecida de trabajo de RC es L*
Producto
Oferta y la cantidad demandada de
laboral demand.
producto es C*
d t
0 L* 24 Trabajo (horas)

41. Maximización de utilidad y
maximización de ganancias
Maximización de ganancias:
– w = PML
– cantidad de producto ofrecido = C*
– cantidad de trabajo demandado =
L*

42. Maximización de utilidad y
maximización de ganancias
Maximización de ganancias:
– w = PML
– cantidad de producto ofrecido = C*
– cantidad de trabajo demandado = L*
Maximización de utilidad:
– w = RMS
– cantidad de producto demandado = C*
C
– cantidad de trabajo ofrecido = L*

43. Maximización de utilidad y
maximización de ganancias
Maximización de utilidad: trabajode cocos y
Mdos. d
Md
se vacían
– w = PML
– cantidad de producto ofrecido = C*
– Cantidad de trabajo demandado =
L*
Maximización de utilidad:
– w = RMS
– cantidad de producto demandado = C*
– cantidad de trabajo ofrecido = L*

44. Maximización de utilidad y
maximización de ganancias
Cocos RMS = w = PML
C*
Dado w, la cantidad
π* ofrecida de trabajo de RC es L*
f i j C *
y la cantidad demandada y
ofrecida de producto es C*
C
0 L* 24 Trabajo (horas)

45. Eficiencia de Pareto
Debe ser RMS = PML

46. Eficiencia de Pareto
Cocos
RMS ≠ PML
0 24 Trabajo (horas)

47. Eficiencia de Pareto
Cocos
RMS ≠ PML
Cestas de consumo preferido
0 24 Trabajo (horas)

48. Eficiencia de Pareto
Cocos
RMS = PML
0 24 Trabajo (horas)

49. Eficiencia de Pareto
Cocos
RMS = PML. Pendiente común ⇒ tasa de salario
relativo w que implementa el
plan de eficiencia de Pareto a
través de una fijación de precio
desentralizado
0 24 Trabajo (horas)

50. Tecnologías no convexas
¿Se cumplen los teoremas de
bienestar si las firmas tienen
tecnologías no convexas?

51. Tecnologías no convexas
¿Se cumplen los teoremas de
bienestar si las firmas tienen
tecnologías no convexas?
El primer teorema del bienestar no se
i d l bi
g
basa en las firmas con tecnologías
convexas

52. Tecnologías no convexas
Cocos
RMS = PML La pendiente común ⇒ tasa de
salario relativo w que
implementa el plan de
eficiencia de Pareto a
través de una fijación de
precios descentralizado
0 24 Trabajo (horas)

53. Tecnologías no convexas
¿Se cumplen los teoremas de
bienestar si las firmas tienen
tecnologías no convexas?
El segundo teorema requiere que las
d i l
tecnologías de las firmas sean
g
convexas

54. Tecnologías no convexas
Cocos
RMS = PML. La asignación óptima de Pareto
no puede implementarse
por un equilibrio
competitivo
0 24 Trabajo (horas)

55. Ventaja Comparativa
Dos agentes, RC y MF
RC puede producir 20 cocos o 30
pescados
MF puede producir hasta 50 cocos o
25 pescados

56. Ventaja Comparativa
C RC
20
30 P
C MF
50
25 P

57. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescados, coste de oport. De
un pescado más es renunciar a 2/3 cocos
30 P
C MF
50
25 P

58. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescados, coste de oport. De
un pescado más es renunciar a 2/3 cocos
30 F
C MF
50
RMTP = -2 cocos/pescados, el coste de oport. De
2 / d l t d t D
un pescado adicional es renunciar a 2 cocos
25 F

59. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescados, coste de oport. De
un pescado más es renunciar a 2/3 cocos
RC tiene ventaja comparativa
30 P de coste de oportunidad al
p
C MF
50 producir pescados
RMTP = -2 cocos/pescados, el coste de oport. De
2 / d l t d t D
un pescado adicional es renunciar a 2 cocos
25 P

60. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescado, coste de oport. de
un coco adicional es renunciar a 3/2 pescados
30 P
C MF
50
25 P

61. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescado, coste de oport. de
un coco adicional es renunciar a 3/2 pescados
30 P
C MF
50
RMTP = -2 cocos/pescados, coste de oport. de
2 / d t d t d
un coco adicional es renunciar a 1/2 pescados
25 P

62. Ventaja Comparativa
C RC
20 RMTP = -2/3 cocos/pescado, coste de oport. de
un coco adicional es renunciar a 3/2 pescados
30 P
C MF
50
RMTP = -2 cocos/pescados, coste de oport. de
2 / d t d t d
un coco adicional es renunciar a 1/2 pescados
MF tiene ventaja comparativa de
coste de oportunidad al
producir cocos
25 P

63. Ventaja Comparativa
C RC
Economía
C Usar RC para producir
20
p
pescado antes que usar
q
70 MF
30 P
C Usar MF para
MF 50
50 producir cocos
antes de usar RC
30 55 P
25 P

64. Ventaja Comparativa
C RC
Economía
C Con coste de oport. bajos
20
los productores resultan
p
70 en una f.p.p. que es
30 P cóncava al origen
C MF 50
50
30 55 P
25 P

65. Ventaja Comparativa
C Economía
Más productores con
diferentes costes de
oportunidad suavizan
la f.p.p.
F

66. Coordinando Producción &
Consumo
La f.p.p. contiene muchas cestas de
producción técnicamente eficientes
¿Cuáles son Pareto eficientes para
los
l consumidores?
id ?

67. Coordinando Producción &
Cocos Consumo
Cesta de producto es
C′ ( P′, C ′)
P′ Pescado

68. Coordinando Producción &
Cocos Consumo
Cesta de producto es( P′, C ′)
C′ y es la dotación agregada
pa a a distribución os
para la d st buc ó a los
consumidores RC y MF
P′ Pescado

69. Coordinando Producción &
Cocos Consumo
Cesta de producto es( F ′, C ′)
OMF
C′ y es la dotación agregada
para la distribución a los
consumidores RC y MF
ORC
P′ Pescado

70. Coordinando Producción &
Cocos Consumo
Asignar ( P′, C ′) eficientemente;
A i fi i t t
OMF digamos ( P′ , C ′ ) a RC
C′ RC RC
′
CRC
ORC
′
PRC P′ Pescado

71. Coordinando Producción &
Cocos Consumo
′
PMF Asignar ( P ′ , C ′ ) eficientemente;
OMF ′ ′
digamos ( PRC , C RC ) a RC y
C′
( P ′ , C ′ )a MF
MF MF
′
CRC ′
CMF
ORC
′
PRC P′ Pescado

72. Coordinando Producción &
Cocos Consumo
′
PMF
OMF
C′
′
CRC ′
CMF
ORC
′
PRC P′ Pescado

73. Coordinando Producción &
Cocos Consumo
′
PMF
C′ OMF
′
CRC ′
CMF
ORC P′ Pescado
′
PRC

74. Coordinando Producción &
Cocos Consumo
′
PMF OMF
C′
′
CRC ′
CMF
ORC
′
PRC P' Pescado

75. Coordinando Producción &
Cocos Consumo
′
PMF OMF RMS ≠ RMTP
C′
′
CRC ′
CMF
ORC
′
PRC P′ Pescado

76. Coordinando Producción &
Cocos Consumo
′
PMF O bien produce ( P′′, C ′′)
).
OMF
C′
O
O’MF
C ′′
′
CRC ′
CMF
ORC
′
PRC P′ P′′ Pescado

77. Coordinando Producción &
Cocos Consumo
′
PMF O bien produce( P′′, C ′′)
).
OMF
C′
O
O’MF
C ′′
′
CRC ′
CMF
ORC
′
PRC P′ P′′ Pescado

78. Coordinando Producción &
Cocos Consumo
′
PMF
OMF O bien produce ( F ′′, C ′′).
C′ Da a MF la misma asignac.
′
PMF O
O’MF
C ′′ que antes
′
CRC ′
CMF
′
CMF
ORC ′ P′
PRC P′′ Pescado

79. Coordinando Producción &
Cocos Consumo
′
PMF O bien produce ( F ′′, C ′′)
).
OMF
C′ Da a MF la misma asignac.
C ′′ ′
PMF O
O’MF que antes. La
antes
utilidad de MF
no cambia
′
CRC ′
CMF
′
CMF
ORC ′
PRC P′ P′′ Pescado

80. Coordinando Producción &
Cocos Consumo
O bien produce ( F ′′, C ′′)
).
OMF Da a MF la misma asignac.
′
PMF O
O’MF que antes. La
antes
C ′′ utilidad de MF
no cambia
′
CMF
ORC
P′′ Pescado

81. Coordinando Producción &
Cocos Consumo
OMF O bien produce ( F ′′, C ′′).
bi d
Da a MF la misma asignac.
′
PMF O
O’MF
C ′′ que antes. L
t La
utilidad de MF
no cambia
bi
′′
CRC
′
CMF
ORC ′′
PRC P′′ Pescado

82. Coordinando Producción &
Cocos Consumo
OMF O bien produce ( F ′′, C ′′).
bi d
Da a MF la misma asignac.
′
PMF O
O’MF
C ′′ que antes. L
t La
utilidad de MF
no cambia, la de
bi l d
RC es más alta
′′
CRC
′
CMF
ORC ′′
PRC P′′ Pescado

83. Coordinando Producción &
Cocos Consumo
O bien produce ( F ′′, C ′′)
).
OMF
Da a MF la misma asignac.
′
PMF O
O’MF que antes. La
antes
C ′′
utilidad de MF
no cambia, la de
cambia
RC es más alta;
′′
CRC mejora de
′ Pareto
CMF
ORC ′′
PRC P′′ Pescado

84. Coordinando Producción &
Consumo
RMS ≠ RMTP ⇒ ineficiente
coordinación de producción y
consumo
Así
A í que, RMS = RMTP es necesario
i
para un estado económico óptimo de
Pareto

85. Coordinando Producción &
Cocos Consumo
PMF OMF
C
CRC CMF
ORC
PRC P Pescado

86. Coordinación Descentralizada de
Producción y Consumo
RC y MF son fi
firmas que producen
d
cocos y pescados
RC y MF son también consumidores
que pueden vender trabajo
Precio de coco = pC
Precio de pescado = pF
Salario de RC = wRC
Salario de MF = wMF

87. Coordinación Descentralizada de
Producción y Consumo
LRC, LMF son las cantidades
compradas de trabajo a RC y MF
El problema de maximización de la
firma es escoger C P LRC y LMF para
fi C, P,
maxπ = pC C + pF F − wRC LRC − wMF LMF .

88. Coordinación Descentralizada de
Producción y Consumo
maxπ = pC C + pF F − wRC LRC − wMF LMF .
La ecuación de iso-utilidad es
constantπ = pC C + pF F − wRC LRC − wMF LMF
co s a

89. Coordinación Descentralizada de
Producción y Consumo
maxπ = pC C + pF F − wRC LRC − wMF LMF .
La ecuación de iso-utilidad es
constantπ = pC C + pF F − wRC LRC − wMF LMF
que se puede reescribir
eesc b
π + wRC LRC + wMF LMF pF
C= − F.
pC pC

90. Coordinación Descentralizada de
Producción y Consumo
Cocos
Mayor utilidad
pF
Pendientes −
pC
Pescado
P d

91. Coordinación Descentralizada de
Producción y Consumo
Cocos
El conjunto de
posibilidaddes de
producción de la firma
Pescados
P d

92. Coordinación Descentralizada de
Producción y Consumo
Cocos
Pendientes = −
pF
pC
Pescados
P d

93. Coordinación Descentralizada de
Producción y Consumo
Cocos
Plan de max. de utilidad
pF
Pendiet. = −
pC
Pescados
P d

94. Coordinación Descentralizada de
Producción y Consumo
Cocos
Plan de max. de utilidad
pF
Pend. = −
pC
Pescados
P d

95. Coordinación Descentralizada de
Producción y Consumo
Cocos
Plan de max. de utilidad
pF
Mdos. Competitivos Pend. = −
pC
y max. de utilidad
pF
⇒ RMPT = − .
pC
Pescados
P d

96. Coordinación Descentralizada de
Producción y Consumo
Los mdos. competitivos, la
maximización de utilidad y la
maximización de ganancias hacen
que pF
RMPT = − = RMS ,
pC
la condición necesaria para un
p
estado económico óptimo de Pareto

97. Coordinación Descentralizada de
Producción y Consumo
Cocos
Mdos. competitivos
y max de utilidad
max.
PMF OMF ⇒ pF
C RMS = − .
pC
CRC CMF
ORC PRC P Pescados

98. Coordinación Descentralizada de
Producción y Consumo
Cocos
Mdos. competitivos, max. utilidad
Md titi tilid d
y max. de ganancias ⇒
PMF pF
OMF RMS = − = RMPT
C pC
CRC CMF
ORC PRC P Pescados