Este documento introduce los conceptos de equilibrio general y equilibrio parcial. Explica el intercambio económico entre dos individuos y dos productos usando la caja de Edgeworth. Luego presenta la producción económica de dos productos usando dos factores por parte de dos empresas. Finalmente, define las condiciones para alcanzar el equilibrio general en los mercados de productos y factores.

1. Módulo 13
Equilibrio G
E ilib i General: Introducción
l I t d ió
1

2. Equilibrio General
Equilibrio parcial: no tiene en cuenta
que los cambios en un mercado
puede afectar otros
(productos/factores)
Equilibrio General: analiza la forma
en que las elecciones de los agentes
están coordinadas para todos los
mercados de productos y factores
2

3. Agenda
Intercambio económico
– 2 individuos/consumidores (A y B)
– 2 productores (X e Y)
Producción económica
– 2 productos (X e Y)
– 2 factores (L y K)
Equilibrio General
– 2 individuos/consumidores (A y B)
– 2 productos (X e Y)
– 2 factores (L y K)
3

4. Intercambio Económico
2 Individuos: A y B
2 Productos: X e Y
Suponer un mundo sin producción y con
S i ió
dotaciones fijas de X e Y (de ahí la barra
en l parte superior de X e Y)
la i d
4

5. Caja Edgeworth
1. Mirar al mundo desde la
perspectiva del individuo A
2. Mirar al mundo desde la
perspectiva del individuo B
i d l i di id
3. Combinar los mundos de A y B
para formar la caja de Edgeworth
5

6. Caja Edgeworth
Cantidad
total de
Y
A
U 2
A
U1
Individuo
A
Cantidad
total de X
6

7. Caja Edgeworth
Cantidad
total de X
Individuo
I di id
B
U 1 B
B
U 2 Cantidad
total de
Y
Individuo
A
7

8. Caja Edgeworth
Cantidad
total de X
Individuo
I di id
B
Cantidad
total de
Y
Individuo
A Cada punto dentro de la caja representa una
p j p
asignación particular de los dos productos entre los
8
dos individuos

9. Asignación Pareto Eficiente
Asignación Pareto Eficiente: cada
individuo está sobre la curva de
indiferencia más alta, dada la curva de
indiferencia del otro individuo
9

10. Caja Edgeworth
Individuo
I di id
Cantidad
α B
total de
Y
YB
β
Individuo
A
XA Cantidad
X total de
10

11. Asignación Pareto Ineficiente
α y β son asignaciones Pareto
ineficientes
¿Por qué? Debido a que existen
cambios en las asignaciones,
bi l i i
comenzando desde α o β, que haría
β
que al menos un individuo esté
mejor sin hacer que el otro individuo
esté peor
11

12. Caja Edgeworth
Individuo
I di id
B
Cantidad
total de γ es un
p
punto
Y γ Pareto
eficiente
Individuo
A
Cantidad
X total de
12

13. Asignación Pareto Eficiente
• En el punto/asignación γ:
• El individuo A está sobre la curva de
indiferencia más alta posible dada la curva
de indiferencia de B
d e e ca
• El individuo B está sobre la curva de
indiferencia más alta posible dada la curva
de indiferencia de A
• P l tanto, γ es una asignación Pareto
Por lo t t i ió P t
eficiente
• Nota: las dos curvas de indiferencia son 13
curves son tangentes entre ellas

14. Asignación Pareto Eficiente
Individuo
I di id
B
Cantidad
total de ε ε ψ δ son
Y γ también
asignaciones
δ Pareto
eficientes
Individuo
A
Cantidad
X total de
14

15. Curva Contrato
Individuo
I di id
B
Cantidad
total de ε Uniendo
estos
Y γ
puntos
δ eficientes
de Pareto
resulta la
Individuo curva de
A
Cantidad contrato
X total de
15

16. Curva Contrato
La curva que conecta todas las
asignaciones eficientes de Pareto se
conoce como la curva de contrato
En d
E cada punto sobre l curva d
b la de
contrato, la TMS de A y B son
iguales, es decir,
TMSAxy = TMSBxy
16

17. Mercado
Un “subastador” j t
U “ b t d ” ajusta precios i
del producto (Px y Py) hasta que
se tengan las tres siguientes
co d c o es
condiciones:
P PX
(1) TMS = X
A
(2) TMS B =
PY PY
(3) Demanda de X = X
Demanda de Y = Y
17

18. Mercado: Equilibrio en el
intercambio económico
i bi ó i
Individuo
I di id
B
Cantidad UA
total de
Y UB
PX
PY
Individuo
A
Cantidad
X total de
18

19. Intercambio en la Caja de
Edgeworth: Resumen
Ed h R
XB Individuo
I di id
B
Cantidad
total de
Y
YB
YA
PX
Individuo PY
A
XA Cantidad
X total de
19

20. Producción Económica
Dos firmas producen dos productos
(X e Y)
Las empresas utilizan dos factores
de
d producción, capital (K) and
d ió i l d
trabajo (L)
j ( )
Suponer dotaciones fijas de K y L
20

21. (
(Producción) Caja Edgeworth
) j g
Empresa
Y0 que
Cantidad p
produce
total de bien Y
X1
En los
K Y1
puntos de
tangencia:
g
X0 MRTSXLK=
MRTSYLK
Empresa
que
produce
d
bien X
L Cantidad
total de
21

22. (
(Producción) Caja Edgeworth
) j g
Empresa
que
Cantidad Y0 p
produce
total de bien Y
X1 Se pueden
K Y1 unir todos
estos
puntos
Y* X0 (Pareto)
(P t )
eficientes
para formar
Empresa la curva de
contrato
que
produce
d
bien X
L Cantidad
total de
22

23. Mercado: Equilibrio Producción
Económica
Un “subastador” j t l
U “ b t d ” ajusta los
precios de los factores (Pl = w y
Pk = r) hasta cumplir las tres
co d c o es s gu e tes
condiciones siguientes:
w w
(1) TMST X
= (2) TMST Y =
r
r
(3) Demanda de L = L
Demanda de K = K
23

24. Curva de Posibilidades de
Producción
Cada punto
y
sobre la curva
de posibilidades
de producción
es (Pareto)
eficiente
x
24

25. Curva de Posibilidades de
Producción
y
TMSTXLK = TMSTYLK
x
25

26. Curva de posibilidades de
producción
y Cada punto
de t o
dentro de la
a
curva de
posibilidades
p
de
p
producción
es (Pareto)
ineficiente
x
26

27. Curva de Posibilidades de
Producción
¿Dónde
y ubicarse
sobre la
CPP?
¿Cuánto de X
y cuánto de Y
debe
producirse?
x
27

28. Curva de Posibilidades de
Producción
Pendiente de
y
CPP = ∆y/∆x ¿Cuántas
unidades de Y
se deben
renunciar para
producir una
unidad
adicional de
X?
Tasa marginal de transformación del producto
(TMTP o TMT) 28

29. Equilibrio General
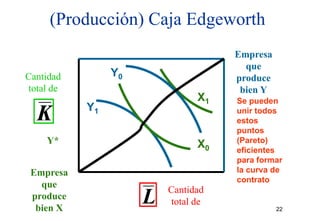
Argumento: en equilibrio, las empresas
p
producirían en el punto sobre la curva de
p
posibilidades de producción en el cual
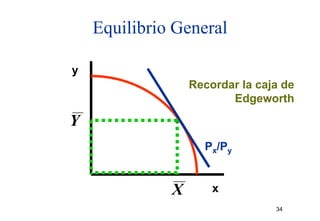
TMTP = Px/Py
Si TMRP < Px/Py ⇒ producir más X y
menos Y
Si TMRP > Px/Py ⇒ producir menos X y
más Y
[Además: TMSxy = Px/Py ⇒ TMTPxy = TMSxy]
29

30. Equilibrio General
y La pendiente de
la restricción =
Px/Py
Px/Py
x
30

31. Equilibrio General
En t
E este punto se
t
y pueden obtener
las
l cantidades
tid d
producidas de x e
y
Px/Py
x
31

32. Equilibrio General
y Esta es la
cantidad de x
producida
Px/Py
X x
32

33. Equilibrio General
y Esta es la
cantidad de y
producida
Y
Px/Py
x
33

34. Equilibrio General
y
Recordar la caja de
Edgeworth
Y
Px/Py
X x
34

35. Equilibrio General
y
Individuo B
Y
Px/Py
Individuo A
X x
35

36. Equilibrio General
y
Individuo B
Y
Px/Py
Individuo A
X x
36

37. Equilibrio General
Recordar que
y
TMSxy= Px/Py
Individuo B
Y
Px/Py
Individuo A
X x
37

38. Equilibrio General
y TMS = TMTP = Px/Py
Y
UA Px/Py
Px/Py UB
X x
38

39. Equilibrio General
Tres Condiciones para el Equilibrio
General:
PX
(1) TMS XY = TMS XY =
A B
PY
PL w
(2) TMS LK = TMS LK =
( ) X Y
=
PK r
PX
(3) TMTPXY = = TMS XY
PY
39

40. Economía del Bienestar
1er Teorema fundamental de economía de
bienestar:
Si todos los mercados son perfectamente
competitivos,
competitivos la asignación de los
recursos serán Pareto eficientes
2do Teorema fundamental de economía del
bienestar:
Cualquier asignación Pareto eficiente
puede obtenerse como resultado de
p
procesos de mercado competitivo, dado
p ,
que la dotación inicial de la economía
puede ser re-distribuida, vía impuestos de
suma fija y subsidios, entre agentes
40