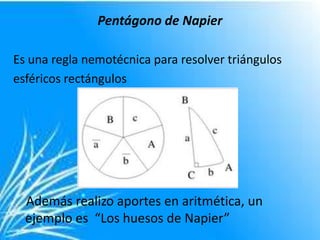
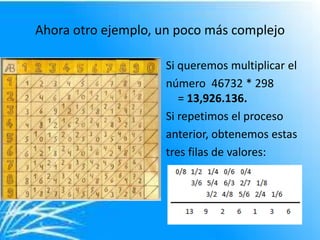
John Napier fue un matemático escocés que vivió entre 1550 y 1617. Es conocido principalmente por haber inventado los logaritmos, una herramienta matemática que simplificó enormemente los cálculos numéricos. También realizó importantes contribuciones a la trigonometría esférica y desarrolló dispositivos como los "Huesos de Napier" para ayudar con las multiplicaciones y divisiones.

1. Nepier John
(1550 – 1617)
Vida y obra
Por Sabrina Dechima

2. Matemático escocés,
nacido en 1550 en el
castillo de Merchinston, y
falleció el 4 de abril de
1617.
Su familia era
aristocrática, y cabe
destacar que no era un
matemático profesional

3. Fue educado en la
universidad de St. Andrews,
a la cual ingreso a los 13
años.
Como no hay registro de
que se halla graduado en
ella, se cree que siguió sus
estudios en otra
perteneciente a Europa
(sobre todo en Alemania y
Países Bajos)

4. Los estudios de Matemática de Nepper fueron
un hobby, ya que estaba más interesado en la
Teología.
Dedicó gran parte de su vida a
inventar sistemas para contener
la invasión de Felipe II de España
Escudo de armas

5. Trabajó durante 20 años en
el invento de los logaritmos
antes de publicar los resultados,
afirmación que permite situar el
origen de sus ideas hacia el año
1594.
Nepper pensó que todas las cifras
se podían expresar de forma
exponencial, con lo que la
multiplicación y la división de
números quedaban
notablemente simplificada,
sumando o restando sus
exponentes

6. La discusión sobre los
logaritmos aparece
publicada en Mirifici
logarithmorum canonis
descripto (Descripción de
la maravillosa regla de los
logaritmos) en 1614. En
esta obra presenta una
tabla de lo logaritmos de
los senos de 0° a 90°, de
minuto a minuto.

7. Una cita de Pierre-Simon Laplace hace
mención y honor al descubrimiento y aplicación
de los logaritmos por Napier:
Con la reducción del trabajo de varios
meses de cálculo a unos pocos días,
el invento de los logaritmos parece haber
duplicado la vida de los astrónomos.
Pierre-Simon Laplace

8. Como obra póstuma
apareció en 1619
Mirifici
logarithmorum
canonis construcio,
donde explica como
construyo la tabla
El nombre Logaritmo
(número de razón) se
debe a él.

9. Realizo grandes aportes a la Geometría esférica,
la cual es la parte de la geometría que estudia los
polígonos que se forman sobre la superficie de la
esfera, en especial, los triángulos.
Su resolución tiene especial relevancia en
astronomía náutica y
navegación para determinar
la posición de un buque en
altamar mediante la
observación de los astros

10. Sus contribuciones a la
Trigonometría esférica,
son (entre otros
aspectos), la llamada
Analogías de Nepier.
(la misma vincula los
lados y ángulos de los
triángulos esféricos; la
cual es logarítmica)

11. Pentágono de Napier
Es una regla nemotécnica para resolver triángulos
esféricos rectángulos
Además realizo aportes en aritmética, un
ejemplo es “Los huesos de Napier”

12. “Los Huesos de Nepier”
Este dispositivo constaba de
una serie de barritas de
madera que contenían las
tablas de multiplicar, de
esta manera evitaba la
memorización de las
mismas y era de gran ayuda
en la realización de
operaciones de
multiplicación y división
con un número elevado
de cifras.

13. Como ejemplo sencillo de su funcionamiento, nos
basaremos en la figura superior, en ella
intentaremos multiplicar el numero
46732 * 7 = 327.124.
Usando este dispositivo colocamos las tablas de
madera como se muestra en la figura, y
obtenemos de ella los valores correspondientes a
la columna del 7, es decir:
2/8 4/2 4/9 2/1 1/4
Y sumamos los números contiguos entre los
símbolos de división:
2 / 8 + 4 / 2 + 4 / 9 + 2 / 1 + 1 / 4 = 327.124

14. Ahora otro ejemplo, un poco más complejo
Si queremos multiplicar el
número 46732 * 298
= 13,926.136.
Si repetimos el proceso
anterior, obtenemos estas
tres filas de valores:

16. Biografía consultada
http://conlamenteabierta.wordpress.com/201
0/09/29/los-huesos-de-napier/#comment-417
http://www.vedrunasevilla.org/vedruna_w/dt
omatematicas/dpt-
matematicas_archivos/descargas/1%C2%BAba
chillerato/TRIGONOMETR%C3%8DA%20I%20(
Teor%C3%ADa).pdf
http://es.wikipedia.org/wiki/Neper

17. Los Matemáticos que
hicieron la historia
Autor: Alejandro Garcia Venturini
Editorial: Ediciones Cooperativas
Segunda Edición. Año: 2004